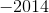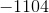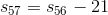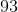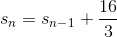All GRE Math Resources
Example Questions
Example Question #1 : How To Find The Next Term In An Arithmetic Sequence
The sequence 
What is the value of 
For this problem, you definitely do not want to "count upwards" to the full value of the sequence. Therefore, the best approach is to consider the general pattern that arises from the general definition:
This means that for every element in the list, each one is 
Now, notice that the first element is:
The second is:
The third could be represented as:
And so forth...
Now, notice that for the third element, there are only two instances of 
This value will always "lag behind" by one. Therefore, for the 
Example Question #1 : Common Difference In Sequences
The sequence 
What is the difference between the 20th and the 30th elements of 
The answer cannot be determined
For this sequence, you do not have a starting point (i.e. 


Now, to find difference between the 20th and the 30th element, it is merely necessary to count the number of twenties that would be added for each of those elements. For instance, the difference between the 21st and the 20th elements is 
Example Question #101 : Arithmetic
Which of the following defines any term in a linear sequence having 

Since this sequence is linear, we know that it will add the same amount for each element. This means that you can evenly divide the difference between the first and the ninth term. Be careful! There will be eight total increases between these terms. (Think this through: 1 to 2, 2 to 3, 3 to 4, etc.)
Thus, we know that the total difference between these terms is:
Now, dividing this among the eight increases that happen, we know:
This means that for each element, we add 
Example Question #691 : Gre Quantitative Reasoning
What is the sum of all of the four-digit integers that can be created with the digits 1, 2, 3, and 4?
48,758
37,891
711,040
482,912
5994
711,040
First we need to find out how many possible numbers there are. The number of possible four-digit numbers with four different digits is simply 4 * 4 * 4 * 4 = 256.
To find the sum, the formula we must remember is sum = average * number of values. The last piece that's missing in this formula is the average. To find this, we can average the first and last number, since the numbers are consecutive. The smallest number that can be created from 1, 2, 3, and 4 is 1111, and the largest number possible is 4444. Then the average is (1111 + 4444)/2.
So sum = 5555/2 * 256 = 711,040.
Example Question #111 : Arithmetic
Quantity A: The sum of all integers from 49 to 98 inclusive.
Quantity B: The sum of all integers from 51 to 99 inclusive.
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
The relationship cannot be determined from the information given.
The two quantities are equal.
For each quantity, only count the integers that aren't in the other quantity. Both quantities include the numbers 51 to 98, so those numbers won't affect which is greater. Only Quantity A has 49 and 50 (for a total of 99) and only Quantity B has 99. Since the excluded numbers from both quantities equal 99, you can conclude that the 2 quantities are equal.
Example Question #112 : Arithmetic
What is the sum of all the integers between 1 and 69, inclusive?
The formula here is sum = average value * number of values. Since this is a consecutive series, the average can be found by averaging only the first and last terms: (1 + 69)/2 = 35.
sum = average * number of values = 35 * 69 = 2415
Example Question #113 : Arithmetic
Quantity A: The sum of all integers from 1 to 30
Quantity B: 465
Quantity A is greater.
The two quantities are equal.
The relationship cannot be determined from the information given.
Quantity B is greater.
The two quantities are equal.
The sum of all integers from 1 to 30 can be found using the formula


Example Question #114 : Arithmetic
The sum of a set of 

We can represent our numbers as:





Thus, we know:
Solve for 
Therefore, the fourth element will be 
Example Question #115 : Arithmetic
The average of five consecutive integers is 
There are two ways to figure out this list of integers. On the one hand, you might know that the average of a set of consecutive integers is the "middle value" of that set. So, if the average is 

Another way to figure this out is to represent your integers as:
The average of these values will be all of these numbers added together and then divided by 
Multiply both sides by 
Finish solving:
This means that the largest value is:
Example Question #116 : Arithmetic
If the sum of four consecutive numbers is 38, what is the mean of the largest and the smallest of the four numbers?
11.75
9.5
11
8.75
10.5
9.5
The sum of 4 consecutive numbers being 38 can be written as the following equation.
We can simplify this to solve for x.
This tells us that the smallest number is 8 and the largest is (8 + 3) = 11. From this, we can find their mean.
All GRE Math Resources