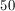GRE Math : Algebraic Fractions

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1021 : Algebra

Simplify the following expression:

$\frac{4x^6}{8x^3}$

Possible Answers:

Correct answer:

Explanation:

Following this equation, you divide 4 by 8 to get 1/2. When a variable is raised to an exponent, and you are dividing, you subtract the exponents, so 6 – 3 = 3.

Report an Error

Example Question #12 : How To Simplify A Fraction

Reduce the fraction:

$\frac{12}{96}$

Possible Answers:

$\frac{1}{8}$

$\frac{3}{24}$

$\frac{7}{12}$

$\frac{1}{4}$

$\frac{4}{16}$

Correct answer:

$\frac{1}{8}$

Explanation:

The numerator and denominator are both divisible by 12. Thus, we divide both by 12 to get our final answer.

If we instead divide by another common factor, we may need to complete the process again to make sure that we have completely reduced the fraction.

In mathematical words we get the following:

$\frac{12}{96}=\frac{1 \cdot 12}{8 \cdot 12}=\frac{1}{8}$

Report an Error

Example Question #12 : How To Simplify A Fraction

Simplify.

$\frac{(x^3+8x^2-69x-252)}{(x^2+5x-84)}$

Possible Answers:

$\frac{(x+3)}{(x-7)}$

x-3

x+3

$\frac{1}{(x-7)}$

x+12

Correct answer:

x+3

Explanation:

When we factor the numerator and denominator, we get:

$\frac{(x-7)(x+12)(x+3)}{(x-7)(x+12)}$ .

After cancelling (x-7)(x+12) , we are left with x+3 .

Report an Error

Example Question #41 : Algebraic Fractions

Which of the following fractions is between $\frac{1}{2}$ and $\frac{3}{4}$ ?

Possible Answers:

$\frac{5}{12}$

$\frac{13}{16}$

$\frac{10}{12}$

$\frac{9}{16}$

$\frac{7}{16}$

Correct answer:

$\frac{9}{16}$

Explanation:

With common denominators, the range is from

$\frac{6}{12} to \frac{9}{12}$

$\frac{8}{16} to \frac{12}{16}$ .

The only fraction that falls in either of these ranges is $\frac{9}{16}$ .

Report an Error

Example Question #2 : How To Solve For A Variable As Part Of A Fraction

$\dpi{100} \small \frac{4 }{x} = \frac{2}{25}$

Find x.

Possible Answers:

$\dpi{100} \small 0.25$

None

$\dpi{100} \small \frac{8}{25}$

$\dpi{100} \small 50$

$\dpi{100} \small \frac{25}{8}$

Correct answer:

$\dpi{100} \small 50$

Explanation:

Cross multiply:

$\dpi{100} \small 4 \times 25 = 2x$

$\dpi{100} \small 100 = 2x$

$\dpi{100} \small x = 50$

Report an Error

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

The numerator of a fraction is the sum of 4 and 5 times the denominator. If you divide the fraction by 2, the numerator is 3 times the denominator. Find the simplified version of the fraction.

Possible Answers:

$\frac{1}{3}$

$\frac{1}{2}$

Correct answer:

Explanation:

Let numerator = N and denominator = D.

According to the first statement,

N = (D x 5) + 4.

According to the second statement, N / 2 = 3 * D.

Let's multiply the second equation by –2 and add itthe first equation:

–N = –6D

+[N = (D x 5) + 4]

–6D + (D x 5) + 4 = 0

–1D + 4 = 0

D = 4

Thus, N = 24.

Therefore, N/D = 24/4 = 6.

Report an Error

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

If $\frac{(x-7)}{2x} = \frac{5}{9}$ , what is the value of ?

Possible Answers:

$-\frac{35}{13}$

$\frac{73}{9}$

Correct answer:

Explanation:

Start by cross multiplying to get the equation

$5\cdot2x=(x-7)\cdot 9$

10x = 9x-63 .

Then simplify by subtracting from each side to get the solution,

x = -63 .

Report an Error

Example Question #1575 : Gre Quantitative Reasoning

If $\frac{x}{4} = 15$ , then what is $\frac{3x}{5} - 36$ equal to?

Possible Answers:

Correct answer:

Explanation:

We start by solving for x in $\frac{x}{4} = 15$ by multiplying 4 and 15, which gives us x=60 .

Then substituting 60 for x in,

$\frac{3x}{5} - 36$ gives us

$\frac{180}{5} - 36=36-36=0$ which equals 0.

Report an Error

Example Question #42 : Algebraic Fractions

If $\frac{x-p}{r} = \frac{q}{pr}$ , and x, p, q, r > 0 , what is the value of ?

Possible Answers:

$x=q + \frac{r}{p}$

$x=\frac{q}{p} + p$

$x=\frac{p}{q} + r$

x=q + r

$x=\frac{q}{p} - q$

Correct answer:

$x=\frac{q}{p} + p$

Explanation:

Start by cross multiplying which gives us qr = pr(x-p) .

Simplify by dividing both sides by which gives us q = p(x-p) .

Isolate by dividing both sides by and then adding to both sides, which gives us $x = \frac{q}{p} +p$ .

Report an Error

Example Question #2 : How To Solve For A Variable As Part Of A Fraction

If $\frac{2}{3x} = \frac{4x}{5}$ , and x>0 what is the value of ?

Possible Answers:

$\sqrt{10}$

$\frac{15}{8}$

$\sqrt{\frac{5}{6}}$

$-\sqrt{\frac{5}{6}}$

$\frac{8}{15}$

Correct answer:

$\sqrt{\frac{5}{6}}$

Explanation:

Start by cross multiplying which gives us

4x(3x)=2(5)

$12x^{^{2}} = 10$ .

Divide both sides by 12 and simplify which gives us $x^{^{2}} = \frac{5}{6}$ .

Since x>0 , we only take the positive square root as the solution, ${}x = {\sqrt{\frac{5}{6}}}$ .

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Seattle, English Tutors in New York City, LSAT Tutors in San Diego, GRE Tutors in San Diego, SSAT Tutors in San Diego, Algebra Tutors in Chicago, Biology Tutors in Atlanta, Spanish Tutors in Seattle, Reading Tutors in Dallas Fort Worth, Spanish Tutors in Atlanta

Popular Courses & Classes

MCAT Courses & Classes in Seattle, MCAT Courses & Classes in Los Angeles, SAT Courses & Classes in Chicago, SAT Courses & Classes in New York City, GMAT Courses & Classes in New York City, MCAT Courses & Classes in Denver, LSAT Courses & Classes in Denver, LSAT Courses & Classes in Atlanta, ISEE Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Phoenix

Popular Test Prep

ACT Test Prep in Atlanta, SSAT Test Prep in Houston, SSAT Test Prep in Atlanta, ACT Test Prep in Seattle, ACT Test Prep in Boston, MCAT Test Prep in Atlanta, GMAT Test Prep in Washington DC, LSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in New York City, GMAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : Algebraic Fractions

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1021 : Algebra

Example Question #12 : How To Simplify A Fraction

Example Question #12 : How To Simplify A Fraction

Example Question #41 : Algebraic Fractions

Example Question #2 : How To Solve For A Variable As Part Of A Fraction

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Example Question #1575 : Gre Quantitative Reasoning

Example Question #42 : Algebraic Fractions

Example Question #2 : How To Solve For A Variable As Part Of A Fraction

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details