GMAT Math : Right Triangles
Study concepts, example questions & explanations for GMAT Math
All GMAT Math Resources
Example Questions
Example Question #277 : Geometry
Calculate the area of the following right triangle, leave in terms of 
(Not drawn to scale.)
The equation for the area of a right triangle is:
In this case, our values are:
Plugging this into the equation leaves us with:
which can be rewritten as
Example Question #4 : Calculating The Area Of A Right Triangle
A right triangle has a hypotenuse of 13 and a base of 12. Calculate the area of the triangle.
In order to calculate the area of a right triangle, we need to know the height and the base. We are only given the length of the base, so we first need to use the Pythagorean theorem with the given hypotenuse to find the length of the height:
Now that we have the height and the base, we can plug these values into the formula for the area of a right triangle:
Example Question #31 : Triangles
Find the area of a triangle whose base is 
To find the area, use the following formula:
Example Question #1 : Calculating Whether Right Triangles Are Congruent
A right triangle has a height of 
In order for two triangles to be congruent, they must be identical. That is, the lengths of the corresponding sides of two congruent triangles must be equal. This means that in order for a triangle to be congruent to one with a height of 
Example Question #2 : Calculating Whether Right Triangles Are Congruent
A given right triangle has a base of 
None of the above.
In order for two right triangles to be congruent, the bases and heights must have identical lengths. Since we have a given right triangle with a base of 
Example Question #523 : Gmat Quantitative Reasoning
A given right triangle has a height of 
None of the above.
In order for two right triangles to be congruent, the hypotenuses and acute angles must be identical. Since we have a given right triangle with an acute angle of 
Example Question #3 : Calculating Whether Right Triangles Are Congruent
A given right triangle has a base of 
None of the above.
In order for two right triangles to be congruent, the bases and heights must have identical lengths. Since we have a given right triangle with a base of 
Example Question #1 : Calculating The Height Of A Right Triangle
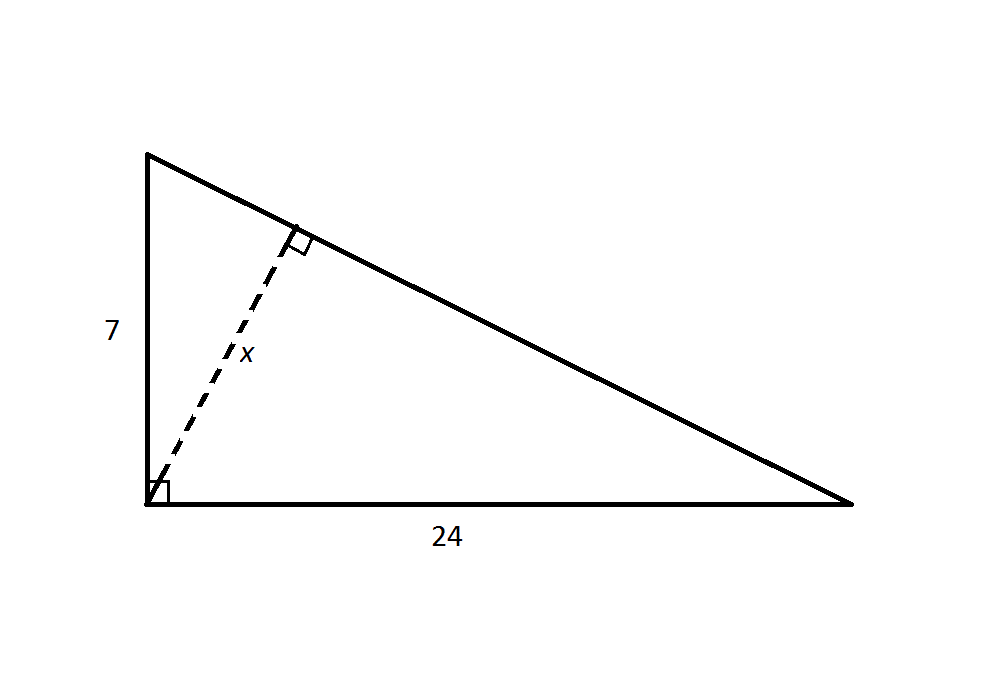
Note: Figure NOT drawn to scale
Refer to the above diagram.
Calculate
Insufficient information is given to calculate 
The hypotenuse of the large right triangle is
The area of the large right triangle is half the product of its base and its height. The base can be any side of the triangle; the height would be the length of the altitude, which is the perpendicular segment from the opposite vertex to that base.
Therefore, the area of the triangle can be calculated as half the product of the legs:
Or half the product of the hypotenuse and the length 
To calculate 
Example Question #2 : Calculating The Height Of A Right Triangle
A right triangle has a base of 8 and an area of 24. What is the height of the triangle?
Using the formula for the area of a right triangle, we can plug in the given values and solve for the height of the triangle:
Example Question #1 : Calculating The Height Of A Right Triangle
Triangle 
The height AE, divides the triangle ABC, in two triangles AEC and AEB with same proportions as the original triangle ABC, this property holds true for any right triangle.
In other words, 
Therefore, we can calculate, the length of AE:
All GMAT Math Resources
