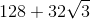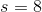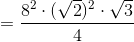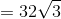GMAT Math : Geometry

Study concepts, example questions & explanations for GMAT Math

Create An Account

All GMAT Math Resources

22 Diagnostic Tests 693 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Calculating The Surface Area Of A Tetrahedron

Tetra_1

The above diagram shows a regular right triangular pyramid. Its base $\bigtriangleup ABC$ is an equilateral triangle; the other three faces are congruent isosceles triangles, with $\overline{VM}$ an altitude of $\bigtriangleup AVC$ . Give the surface area of the pyramid.

Possible Answers:

$36 +216 \sqrt{2}$

$324+ 36 \sqrt{3}$

$252 \sqrt{3}$

$252 \sqrt{2}$

$36 \sqrt{3}+216 \sqrt{2}$

Correct answer:

$36 \sqrt{3}+216 \sqrt{2}$

Explanation:

The base is an equilateral triangle with sidelength 12, so its area can be calculated as follows:

$\frac{12^{2}\cdot \sqrt{3}}{4} = \frac{144 \sqrt{3}}{4} = 36 \sqrt{3}$ .

Each of the three other faces is congruent, with base 12. The area of each is the product of its base and its height. To find the common height, we examine $\bigtriangleup VMC$ , which, since $\overline{VM}$ is an altitude of isosceles $\bigtriangleup AVC$ , is a right triangle with hypotenuse of length 18 and one leg of length $MC = \frac{1}{2} AC = \frac{1}{2} \cdot 12 = 6$ . We can find using the Pythagorean Theorem:

$VM = \sqrt{\left (VC \right )^{2} - \left ( CM\right )^{2}}$

$= \sqrt{18^{2} - 6^{2}}$

$= \sqrt{288}$

$= \sqrt{144} \cdot \sqrt{2}$

$=12\sqrt{2}$

The area of $\bigtriangleup AVC$ is half the product of this height and the base:

$\frac{1}{2} \cdot 12 \cdot 12 \sqrt{2} = 72 \sqrt{2}$

All three lateral faces have this area.

Now add the areas of the four faces:

$36 \sqrt{3}+72 \sqrt{2}+72 \sqrt{2}+72 \sqrt{2} = 36 \sqrt{3}+216 \sqrt{2}$

Report an Error

Example Question #2 : Calculating The Surface Area Of A Tetrahedron

Tetra_1

The cube in the above figure has surface area 384. Give the surface area of the tetrahedron with vertices D,E,G,H , shown in red.

Possible Answers:

128

$96 + 32 \sqrt{3}$

$128 \sqrt{3}$

$128+ 32 \sqrt{3}$

$96 + 64\sqrt{3}$

Correct answer:

$96 + 32 \sqrt{3}$

Explanation:

The surface area formula can be used to find the length of each edge of the cube:

$6s^{2}=384$

$s^{2}= 64$

s= 8

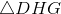
Three faces of the tetrahedron - $\bigtriangleup DHE$ , $\bigtriangleup DHG$ , $\bigtriangleup EHG$ - are right triangles with legs of length 8, so the area of each is half the product of the lengths of their legs:

$\frac{1}{2} \cdot 8 \cdot 8 =32$ .

Each triangle is isosceles, so, by the 45-45-90 Theorem, each of their hypotentuses measures $\sqrt{2}$ times a leg, or $8\sqrt{2}$ . is therefore an equilateral triangle with sidelenghth $8\sqrt{2}$ . Its area can be found as follows:

$A = \frac{s^{2}\sqrt{3}}{4}$

$= \frac{(8\sqrt{2})^{2}\sqrt{3}}{4}$

$= \frac{8^{2}\cdot (\sqrt{2})^{2} \cdot \sqrt{3}}{4}$

$= \frac{64\cdot 2 \cdot \sqrt{3}}{4}$

$= 32 \sqrt{3}$

The total surface area is

$32+32+32+ 32 \sqrt{3} = 96 + 32 \sqrt{3}$

Report an Error

Example Question #501 : Geometry

What is the surface area of a cylinder with a radius of 7 and a height of 3?

Possible Answers:

$\dpi{100} \small 140\pi$

$\dpi{100} \small 120\pi$

$\dpi{100} \small 80\pi$

$\dpi{100} \small 98\pi$

$\dpi{100} \small 42\pi$

Correct answer:

$\dpi{100} \small 140\pi$

Explanation:

All we really need here is to remember the formula for the surface area of a cylinder.

$\dpi{100} \small SA=2\pi r^{2}+2\pi rh=2\pi \left ( 49 \right )+2\pi \left ( 7 \right )\left ( 3 \right )=98\pi +42\pi=140\pi$

Report an Error

Example Question #502 : Geometry

The height of a cylinder is twice the circumference of its base. The radius of the base is 9 inches. What is the surface area of the cylinder?

Possible Answers:

$810 \pi^{2} \textrm{ in}^{2}$

$810 \pi \textrm{ in}^{2}$

$1,620 \pi^{2} \textrm{ in}^{2}$

$\left ( 162 \pi + 648 \pi^{2} \right )\textrm{ in}^{2}$

$\left ( 648 \pi +162 \pi^{2} \right )\textrm{ in}^{2}$

Correct answer:

$\left ( 162 \pi + 648 \pi^{2} \right )\textrm{ in}^{2}$

Explanation:

The radius of the base is 9 inches, so its circumference is $2 \pi$ times this, or $2 \pi \cdot 9 = 18 \pi$ inches. The height is twice this, or $36 \pi$ inches.

Substitute $r = 9 , h = 36 \pi$ in the formula for the surface area of the cylinder:

$A = 2 \pi r (r+h)$

$A = 2 \pi \cdot 9 \cdot (9+36\pi ) = 162 \pi + 648 \pi^{2}$ square inches

Report an Error

Example Question #3 : Calculating The Surface Area Of A Cylinder

Calculate the surface area of the following cylinder.

(Not drawn to scale.)

Possible Answers:

$56\pi$

$32\pi$

$154\pi$

$88\pi$

Correct answer:

$88\pi$

Explanation:

The equation for the surface area of a cylinder is:

$SA=2\pi rh+2\pi r^2$

we plug in our values: r=4, h=7 to find the surface area

$SA=2\pi (4)(7)+2\pi (4)^2$

$SA=2 \pi (28)+32\pi$

$SA=88\pi$

Report an Error

Example Question #1 : Cylinders

Calculate the surface area of the following cylinder.

(Not drawn to scale.)

Possible Answers:

$288\pi$

$360\pi$

$130\pi$

$208\pi$

Correct answer:

$130\pi$

Explanation:

The equation for the surface area of a cylinder is

$SA=2\pi rh+2\pi r^2$

We plug in our values r=5, h=8 into the equation to find our answer.

Note: we were given the diameter of the cylinder (10), in order to find the radius we had to divide the diameter by two.

$SA=2\pi (5)(8)+2\pi (5)^2$

$SA=2\pi (40)+2\pi (25)$

$SA=130\pi$

Report an Error

Example Question #5 : Calculating The Surface Area Of A Cylinder

A cylinder has a height of 9 and a radius of 4. What is the total surface area of the cylinder?

Possible Answers:

$52\pi$

$104\pi$

$132\pi$

$68\pi$

$88\pi$

Correct answer:

$104\pi$

Explanation:

We are given the height and the radius of the cylinder, which is all we need to calculate its surface area. The total surface area will be the area of the two circles on the bottom and top of the cylinder, added to the surface area of the shaft. If we imagine unfolding the shaft of the cylinder, we can see we will have a rectangle whose height is the same as that of the cylinder and whose width is the circumference of the cylinder. This means our formula for the total surface area of the cylinder will be the following:

$SA=2(\pi r^2)+2\pi rh$

$SA=2\pi (4)^2+2\pi (4)(9)$

$SA=32\pi+72\pi$

$SA=104\pi$

Report an Error

Example Question #506 : Geometry

Grant is making a canister out of sheet metal. The canister will be a right cylinder with a height of 150 mm. The base of the cylinder will have a radius of $\frac{5}{\pi}$ mm. If the canister will have an open top, how many square millimeters of metal does Grant need?

Possible Answers:

$1525\text{ } mm^2$

$375+\frac{25}{\pi}\text{ } mm^2$

$1500+\frac{25}{\pi} \text{ } mm^2$

$30+\frac{25}{\pi}\text{ } mm^2$

$1500+\frac{25}{\pi}\text{ } mm^2$

Correct answer:

$1500+\frac{25}{\pi} \text{ } mm^2$

Explanation:

This question is looking for the surface area of a cylinder with only 1 base. Our surface area of a cylinder is given by:

$SA=2\pi rh+2\pi r^2$

However, because we only need 1 base, we can change it to:

$SA=2\pi rh+\pi r^2$

We know our radius and height, so simply plug them in and simplify.

$SA=2\pi \left( \frac{5}{\pi}\right)150+\pi\left(\frac{5}{\pi}\right)^2=1500+\frac{25}{\pi}$

Report an Error

Example Question #4 : Cylinders

Find the surface area of a cylinder whose height is and radius is .

Possible Answers:

$18\pi$

$27\pi$

$45\pi$

$54\pi$

Correct answer:

$54\pi$

Explanation:

To find the surface area of a cylinder, you must use the following equation.

$SA=2\pi{r}h+2\pi{r^2}$

Thus,

$SA=2\pi(3)(6)+2\pi(3^2)=54\pi$

Report an Error

Example Question #8 : Calculating The Surface Area Of A Cylinder

A right circular cylinder has bases of radius $\pi ^{x}$ ; its height is $\pi ^{y}$ . Give its surface area.

Possible Answers:

$2 \pi^{ x+y+1}$

$\pi^{ x+2y+1}$

$\pi ^{ 2x+1 } + \pi ^{x+y+1}$

$\pi ^{ 2y+1 } + \pi ^{x+y+1}$

$\pi^{2 x+y+1}$

Correct answer:

$\pi ^{ 2x+1 } + \pi ^{x+y+1}$

Explanation:

The surface area of a cylinder can be calculated from its radius and height as follows:

$A = \pi r ^{2} + \pi rh$

Setting $r = \pi^{x}$ and $h = \pi ^{x}$ :

$A = \pi \cdot ( \pi^{x}) ^{2} + \pi \cdot \pi^{x} \cdot \pi^{y}$

$A = \pi ^{1 } \cdot \pi^{2x} + \pi ^{1 } \cdot \pi^{x} \cdot \pi^{y}$

$A = \pi ^{1 +2x} + \pi ^{1+x+y}$ or $A = \pi ^{ 2x+1 } + \pi ^{x+y+1}$

Report an Error

All GMAT Math Resources

22 Diagnostic Tests 693 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Los Angeles, Reading Tutors in New York City, Chemistry Tutors in Miami, ISEE Tutors in Dallas Fort Worth, ACT Tutors in Atlanta, MCAT Tutors in San Diego, SSAT Tutors in San Diego, French Tutors in Seattle, Calculus Tutors in Dallas Fort Worth, Statistics Tutors in New York City

Popular Courses & Classes

MCAT Courses & Classes in Houston, Spanish Courses & Classes in Washington DC, LSAT Courses & Classes in Houston, GRE Courses & Classes in San Diego, ISEE Courses & Classes in Houston, LSAT Courses & Classes in Los Angeles, GRE Courses & Classes in Seattle, SAT Courses & Classes in New York City, SAT Courses & Classes in Philadelphia, SAT Courses & Classes in Los Angeles

Popular Test Prep

GMAT Test Prep in Washington DC, ACT Test Prep in Phoenix, SSAT Test Prep in Dallas Fort Worth, GRE Test Prep in San Francisco-Bay Area, SSAT Test Prep in Philadelphia, GRE Test Prep in Denver, ACT Test Prep in Miami, GRE Test Prep in Seattle, SSAT Test Prep in Boston, LSAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GMAT Math : Geometry

Study concepts, example questions & explanations for GMAT Math

All GMAT Math Resources

Example Questions

Example Question #3 : Calculating The Surface Area Of A Tetrahedron

Example Question #2 : Calculating The Surface Area Of A Tetrahedron

Example Question #501 : Geometry

Example Question #502 : Geometry

Example Question #3 : Calculating The Surface Area Of A Cylinder

Example Question #1 : Cylinders

Example Question #5 : Calculating The Surface Area Of A Cylinder

Example Question #506 : Geometry

Example Question #4 : Cylinders

Example Question #8 : Calculating The Surface Area Of A Cylinder

All GMAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details