GED Math : 2-Dimensional Geometry
Study concepts, example questions & explanations for GED Math
All GED Math Resources
Example Questions
Example Question #53 : Triangles
You want to build a garden in the shape of a right triangle. If the two arms will be 6ft and 8ft, how much area will the garden take up?
You want to build a garden in the shape of a right triangle. If the two arms will be 6ft and 8ft, how much area will the garden take up?
To find the area of a triangle, use the following formula.
Note that in a right triangle, our two arms correspond to our base and our height. Furthermore, it does not matter which is which, because when we multiply, order does not matter.
So, to find our area, simply plug in and simplify.
So, our answer is 24 ft squared
Example Question #54 : Triangles
What is the area of an equilateral triangle that has a perimeter of 
Start by finding the length of a side of the triangle.
Next, recall how to find the area of an equilateral triangle.
Plug in the length of the side to find the area.
Example Question #231 : 2 Dimensional Geometry
If the height of a triangle is twice the length of the base, and the base length is 3.5 inches, what is the area of the triangle?
First we need to know that the formula for area of a triangle:
We know that our base is 3.5 inches, and our height is twice that, which is 7 in.
Now we can plug in our base and height to the equation
Multiply and solve
Example Question #232 : 2 Dimensional Geometry
What is the area of a triangle with a height that is three times the length of the base, if the base is 4cm?
First we need to recall the formula for area of a triangle:
We know that our base is 4cm, and our height is 3 times the length of the base, since 4x3=12 we know that our height is 12cm
Now we can plug in our numbers
First we multiply 4 and 12
Next we distribute the fraction which is the same as dividing in half
Notice our answer is in centimeters since we multiplied two terms measured in centimeters
Example Question #1 : Angles And Triangles
Which of the following can be the measures of the three angles of an acute isosceles triangle?
For the triangle to be acute, all three angles must measure less than 
In an isosceles triangle, at least two angles are congruent, so we can eliminate 
The degree measures of the three angles of a triangle must total 180, so, since 
Example Question #231 : Geometry And Graphs
Note: Figure NOT drawn to scale.
Refer to the above triangle. Evaluate 
The degree measures of a triangle total 
Example Question #55 : Triangles
Note: Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
The degree measures of the interior angles of a triangle total 
Three angles with measures 
Example Question #232 : Geometry And Graphs
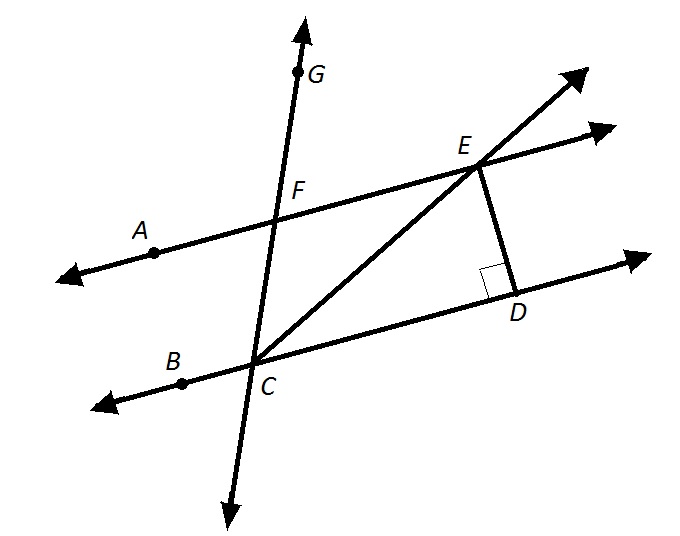
Figure drawn to scale.
Refer to the above diagram.
Which of the following is a valid description of 
Right
Obtuse
Acute
Equiangular
Obtuse
One of the angles of 
Example Question #61 : Triangles
Refer to the above diagram.
Which of the following is a valid description of 
Equiangular
Acute
Obtuse
Right
Right
One of the angles of 
Example Question #3 : Angles And Triangles
Which of the following follows from the fact that 
A congruency statement about two triangles implies nothing about the relationship between two angles of one of the triangles, so 
Also, letters in the same position between the two triangles refer to corresponding - and subsequently, congruent - angles. Therefore,
Of the given choices, only 
All GED Math Resources
