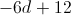All Common Core: 6th Grade Math Resources
Example Questions
Example Question #7 : Apply The Properties Of Operations To Generate Equivalent Expressions: Ccss.Math.Content.6.Ee.A.3
Simplify the following expression using the distributive property.
Distributive property is used to multiply a single term by two or more terms inside a set of parenthesis. Multiply the outside term (5) by 7
Then multiply the outside term (5) by 9.
Combine the two remaining terms by keeping the sign that was originally inside the parenthesis.
Example Question #3 : Distributive Property
Which of the following is equivalent to 
We need to distribute -3 by multiplying both terms inside the parentheses by -3.:

Now we can multiply and simplify. Remember that multiplying two negative numbers results in a positive number:
Example Question #11 : High School Math
Distribute:
Remember that a negative multiplied by a negative is positive, and a negative multiplied by a positive is negative.
Distribute the 
Example Question #291 : Expressions & Equations
Solve the equation using the distributive property.
First, we must use the distributive property on both sides of the equation.
The distributive property states:
Therefore:
Now, we can solve the expression like a two-step equation with variables on both sides. Do not forget the properties of equality and perform the same operations on both sides.
Subtract 

Simplify.
Now, the problem is a one-step equation.
Add 

Solve.
Check the answer by substituting it back into the original equation. Both sides should equal to each other.
Example Question #292 : Expressions & Equations
Simplify using the distributive property:
First, we must use the distributive property on both sides of the equation.
The distributive property states:
In other words, we can take the factor on the outside of the parentheses and multiply it by each term inside the parentheses.
Therefore:
Simplify.
Example Question #11 : Apply The Properties Of Operations To Generate Equivalent Expressions: Ccss.Math.Content.6.Ee.A.3
Select the expression that is equal to
To solve this problem we need to use the distributive property. This property is used to multiply a term outside of a set of parentheses by each of the terms in the parentheses.
Now we have
This expression is simplified because we cannot add 



Example Question #12 : Apply The Properties Of Operations To Generate Equivalent Expressions: Ccss.Math.Content.6.Ee.A.3
Select the expression that is equal to
To solve this problem we need to use the distributive property. This property is used to multiply a term outside of a set of parentheses by each of the terms in the parentheses.
Now we have
This expression is simplified because we cannot add 



Example Question #751 : Grade 6
Select the expression that is equal to
To solve this problem we need to use the distributive property. This property is used to multiply a term outside of a set of parentheses by each of the terms in the parentheses.
Now we have
This expression is simplified because we cannot add 



Example Question #293 : Expressions & Equations
Select the expression that is equal to
To solve this problem we need to use the distributive property. This property is used to multiply a term outside of a set of parentheses by each of the terms in the parentheses.
Now we have
This expression is simplified because we cannot add 

Example Question #294 : Expressions & Equations
Select the expression that is equal to
To solve this problem we need to use the distributive property. This property is used to multiply a term outside of a set of parentheses by each of the terms in the parentheses.
Now we have
This expression is simplified because we cannot add 



All Common Core: 6th Grade Math Resources