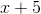Call Now to Set Up Tutoring:

(888) 888-0446

College Algebra : Dividing Polynomials

Study concepts, example questions & explanations for College Algebra

Create An Account

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Simplifying Polynomials

Divide the trinomial below by .

$18x^{2}+ 9x -3$

Possible Answers:

$2x^{2}+ x -\frac{1}{3}$

$2x+1-\frac{1}{3x}$

$-3x+1+\frac{1}{2x}$

$2x+1-\frac{3}{x}$

-x+1

Correct answer:

$2x+1-\frac{1}{3x}$

Explanation:

$18x^{2}+ 9x -3$

We can accomplish this division by re-writing the problem as a fraction.

$\frac{18x^2+9x-3}{9x}$

The denominator will distribute, allowing us to address each element separately.

$\frac{18x^{2}+ 9x -3}{9x}=\frac{18x^{2}}{9x}+\frac{ 9x}{9x}-\frac{3}{9x}$

Now we can cancel common factors to find our answer.

$(\frac{18}{9}* \frac{x^{2}}{x})+1-(\frac{3}{9}* \frac{1}{x})$

$2x+1-\frac{1}{3x}$

Report an Error

Example Question #1 : Polynomial Functions

Simplify:

$y=\frac{(x^2-16)(x+7)}{x+4}+(x-1)^2+13$

Possible Answers:

$y=\frac{(x^2-16)(x+7)}{x+4}+x^2-2x+14$

y=x^2-x-14

y=2x^2+x-14

$y=\frac{x^3+7x^2-16x-112}{x+4}+(x-1)^2+13$

y=2(x^2+x-7)

Correct answer:

y=2x^2+x-14

Explanation:

$y=\frac{(x^2-16)(x+7)}{x+4}+(x-1)^2+13$

First, factor the numerator of the quotient term by recognizing the difference of squares:

$y=\frac{(x-4)(x+4)(x+7)}{x+4}+(x-1)^2+13$

Cancel out the common term from the numerator and denominator:

y=(x-4)(x+7)+(x-1)^2+13

FOIL (First Outer Inner Last) the first two terms of the equation:

y=x^2+7x-4x-28+x^2-2x+1+13

Combine like terms:

y=2x^2+x-14

Report an Error

Example Question #2 : Dividing Polynomials

Divide:

$(x^{3} -23x+10) \div (x-5)$

Possible Answers:

$x^{2} + 5x + 2 + \frac{20}{x-5}$

$x^{2}+1+\frac{12}{x-5}$

$x^{2} + 5x + 2$

$x^{2} - 5x + 16 - \frac{73}{x-5}$

$x^{2} - 5x + 16 + \frac{87}{x-5}$

Correct answer:

$x^{2} + 5x + 2 + \frac{20}{x-5}$

Explanation:

First, rewrite this problem so that the missing $x^{2}$ term is replaced by $0x^{2}$

$(x^{3} + 0x^{2} -23x+10) \div (x-5)$

Divide the leading coefficients:

$x^{3} \div x = x^{2}$ , the first term of the quotient

Multiply this term by the divisor, and subtract the product from the dividend:

$x^{2} (x-5) = x^{3} -5x^{2}$

$(x^{3} + 0x^{2} -23x+10) - (x^{3} -5x^{2}) = 5x^{2}-23x+10$

Repeat this process with each difference:

$5x^{2} \div x = 5x$ , the second term of the quotient

$5x (x-5) = 5 x^{2} -25$

$5x^{2}-23x+10 - ( 5x^{2} -25x) = 2x+10$

One more time:

$2x \div x = 2$ , the third term of the quotient

2 (x-5) = 2x-10

2x+10 - (2x-10) = 20 , the remainder

The quotient is $x^{2} + 5x + 2$ and the remainder is ; this can be rewritten as a quotient of

$x^{2} + 5x + 2 + \frac{20}{x-5}$

Report an Error

Example Question #2 : Polynomial Functions

Divide:

$\left (x^{2} + 6x -7 \right )\div (x+3)$

Possible Answers:

$x+ 3 + \frac{16}{x+3}$

$x+ 3 - \frac{16}{x+3}$

$x- 3 + \frac{2}{x+3}$

$x- 3 - \frac{16}{x+3}$

$x+ 3 + \frac{2}{x+3}$

Correct answer:

$x+ 3 - \frac{16}{x+3}$

Explanation:

Divide the leading coefficients to get the first term of the quotient:

$x^{2} \div x = x$ , the first term of the quotient

Multiply this term by the divisor, and subtract the product from the dividend:

$x (x+3) = x^{2} + 3x$

$\left (x^{2} + 6x -7 \right ) - (x^{2}+3x) = 3x -7$

Repeat these steps with the differences until the difference is an integer. As it turns out, we need to repeat only once:

$3x\div x = 3$ , the second term of the quotient

3 (x+3) = 3x + 9

(3x -7) - (3x + 9) = -16 , the remainder

Putting it all together, the quotient can be written as $x+ 3 - \frac{16}{x+3}$ .

Report an Error

Example Question #3 : Dividing Polynomials

Simplify the following expression:

$\frac{(x-25)}{(x^2-625)}$

Possible Answers:

{x+25}

$\frac{1}{x-25}$

$\frac{1}{x+25}$

$\frac{1}{x^2+25}$

Correct answer:

$\frac{1}{x+25}$

Explanation:

Simplify the following expression:

$\frac{(x-25)}{(x^2-625)}$

To begin, we need to recognize the bottom as a difference of squares. Rewrite it as follows.

$\frac{(x-25)}{(x+25)(x-25)}=\frac{1}{x+25}$

So our answer is:

$\frac{1}{x+25}$

Report an Error

Example Question #4 : Dividing Polynomials

Simplify the following expression:

$\frac{(3x)(3x^2+5x)}{x}$

Possible Answers:

9x^2+15x

9x+15

9x^3+15x^2

3x^2+5x

Correct answer:

9x^2+15x

Explanation:

Simplify the following expression:

$\frac{(3x)(3x^2+5x)}{x}$

First, let's multiply the 3x through:

$\frac{(3x)(3x^2+5x)}{x}=\frac{9x^3+15x^2}{x}$

Next, divide out the x from the bottom:

$\frac{9x^3+15x^2}{x}=9x^2+15x$

So our answer is:

9x^2+15x

Report an Error

Example Question #2 : Dividing Polynomials

$\begin{align*}&\text{Simplify the expresssion:}\\&\frac{x^{2}+30x+225}{x+15}\end{align*}$

Possible Answers:

x+5

x+3

x+15

x+23

Correct answer:

x+15

Explanation:

$\begin{align*}&\textbf{To perform a polynomial long division, it is often}\\&\textbf{helpful to space terms into columns ordered by power.}\\&\textbf{This includes zero terms. For example: }x^2+0x+5\\&\textbf{When performing each division step, choose a coefficient}\\&\textbf{Which eliminates the highest ordered term each time.}\end{align*}\begin{align*}&&&&&&&&\end{align*}\begin{align*}&&&&\mathbf{x}&&\mathbf{+15}\\x&&+15|x^{2}&&+30x&&+225\\&&-(x^{2}&&+15x)\\&&&&15x&&+225\\&&&&-(15x&&+225)\\\end{align*}$

Report an Error

Example Question #7 : Polynomial Functions

$\begin{align*}&\text{Simplify the expresssion:}\\&\frac{x^{2}+x-30}{x-5}\end{align*}$

Possible Answers:

x+1

x+6

x-6

x-26

Correct answer:

x+6

Explanation:

$\begin{align*}&\textbf{To perform a polynomial long division, it is often}\\&\textbf{helpful to space terms into columns ordered by power.}\\&\textbf{This includes zero terms. For example: }x^2+0x+5\\&\textbf{When performing each division step, choose a coefficient}\\&\textbf{Which eliminates the highest ordered term each time.}\end{align*}\begin{align*}&&&&&&&&\end{align*}\begin{align*}&&&&\mathbf{x}&&\mathbf{+6}\\x&&-5|x^{2}&&+x&&-30\\&&-(x^{2}&&-5x)\\&&&&6x&&-30\\&&&&-(6x&&-30)\\\end{align*}$

Report an Error

Example Question #8 : Dividing Polynomials

$\begin{align*}&\text{Simplify the expresssion:}\\&\frac{x^{2}+24x+143}{x+13}\end{align*}$

Possible Answers:

x-27

x-5

x+25

x+11

Correct answer:

x+11

Explanation:

Report an Error

Example Question #4 : Polynomial Functions

$\begin{align*}&\text{Simplify the expresssion:}\\&\frac{x^{5}+x^{4}-353x^{3}-641x^{2}+24832x+98560}{x^{2}-9x-112}\end{align*}$

Possible Answers:

$x^{3}-25x^{2}-22x+27$

$x^{3}-7x^{2}-16x-6$

$x^{3}+28x^{2}+5x-27$

$x^{3}+10x^{2}-151x-880$

Correct answer:

$x^{3}+10x^{2}-151x-880$

Explanation:

$\begin{align*}&\textbf{To perform a polynomial}\\&\textbf{long division, it is often}\\&\textbf{helpful to space terms}\\&\textbf{into columns ordered by power.}\\&\textbf{This includes zero terms.}\\&\textbf{For example: }x^2+0x+5\\&\textbf{When performing each}\\&\textbf{division step, choose a coefficient}\\&\textbf{Which eliminates the highest}\\&\textbf{ordered term each time.}\end{align*}\begin{align*}&&&&&&&&\end{align*}\begin{align*}&&&&&&&&\mathbf{x^{3}}&&\mathbf{+10x^{2}}&&\mathbf{-151x}&&\mathbf{-880}\\x^{2}&&-9x&&-112|x^{5}&&+x^{4}&&-353x^{3}&&-641x^{2}&&+24832x&&+98560\\&&&&-(x^{5}&&-9x^{4}&&-112x^{3})\\&&&&&&10x^{4}&&-241x^{3}&&-641x^{2}\\&&&&&&-(10x^{4}&&-90x^{3}&&-1120x^{2})\\&&&&&&&&-151x^{3}&&479x^{2}&&24832x\\&&&&&&&&-(-151x^{3}&&1359x^{2}&&16912x)\\&&&&&&&&&&-880x^{2}&&7920x&&98560\\&&&&&&&&&&-(-880x^{2}&&7920x&&98560)\\\end{align*}$

Report an Error

View College Algebra Tutors

Reuben
Certified Tutor

University of Alberta, Bachelor of Science, Mathematics.

View College Algebra Tutors

Yucheng
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Mechanical Engineering.

View College Algebra Tutors

Jonathan
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Mathematics.

All College Algebra Resources

5 Diagnostic Tests 84 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Philadelphia, GMAT Tutors in Dallas Fort Worth, Physics Tutors in Denver, SSAT Tutors in Boston, Algebra Tutors in New York City, Computer Science Tutors in New York City, Physics Tutors in Los Angeles, Algebra Tutors in San Diego, Statistics Tutors in Washington DC, Chemistry Tutors in Los Angeles

Popular Courses & Classes

GRE Courses & Classes in Washington DC, LSAT Courses & Classes in Houston, GMAT Courses & Classes in Phoenix, GMAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Phoenix, ISEE Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Boston, ACT Courses & Classes in Philadelphia, Spanish Courses & Classes in Chicago, GMAT Courses & Classes in San Diego

Popular Test Prep

GRE Test Prep in Denver, SAT Test Prep in Philadelphia, ACT Test Prep in Boston, GMAT Test Prep in San Diego, ACT Test Prep in Philadelphia, ISEE Test Prep in San Francisco-Bay Area, SAT Test Prep in Washington DC, GRE Test Prep in San Francisco-Bay Area, ACT Test Prep in Dallas Fort Worth, LSAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

College Algebra : Dividing Polynomials

Study concepts, example questions & explanations for College Algebra

All College Algebra Resources

Example Questions

Example Question #2 : Simplifying Polynomials

Example Question #1 : Polynomial Functions

Example Question #2 : Dividing Polynomials

Example Question #2 : Polynomial Functions

Example Question #3 : Dividing Polynomials

Example Question #4 : Dividing Polynomials

Example Question #2 : Dividing Polynomials

Example Question #7 : Polynomial Functions

Example Question #8 : Dividing Polynomials

Example Question #4 : Polynomial Functions

All College Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: