All Basic Geometry Resources
Example Questions
Example Question #1 : How To Find If Right Triangles Are Congruent
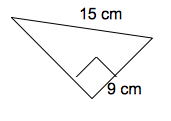
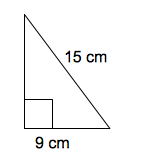
Are the two right triangles congruent?
Yes, by AAS
Yes, by AAA
No, they are not congruent
Yes, by HL
Yes, by AAA
Yes, by HL
Right triangles are congruent if both the hypotenuse and one leg are the same length. These triangles are congruent by HL, or hypotenuse-leg.
Example Question #291 : Right Triangles
Which of the following is not sufficient to show that two right triangles are congruent?
All the sides are congruent.
The hypotenuse and one leg are congruent.
All the angles are congruent.
Both legs are congruent.
All the angles are congruent.
Two right triangles can have all the same angles and not be congruent, merely scaled larger or smaller. If all the side lengths are multiplied by the same number, the angles will remain unchanged, but the triangles will not be congruent.
Example Question #1471 : Plane Geometry
Which of the following pieces of information would not allow the conclusion that


To determine the answer choice that does not lead to congruence, we should simply use process of elimination.
If 





Similarly, if 

If 
Finally, if 

The only remaining choice is the case where 
Example Question #1472 : Plane Geometry
Complete the congruence statement

Since we know that 


We are given that 


Therefore, we have enough evidence to conclude congruence by Angle-Side-Angle. Vertex 





Example Question #5 : How To Find If Right Triangles Are Congruent
Figures 


Are 

Yes.
No.
There is not enough information given to answer this question.
Yes.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of 




Example Question #1 : How To Find If Right Triangles Are Congruent
Figures 


Are 

No.
Yes.
There is not enough information given to answer this question.
Yes.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of 
Simplify the ratio by dividing by
Thus, the corresponding sides are in the ratio 

Example Question #1 : How To Find If Right Triangles Are Congruent
Figures 


Are 

No.
There is not enough information given to answer this question.
Yes.
Yes.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal, and the measures of two angles. We know that 


Example Question #8 : How To Find If Right Triangles Are Congruent
Figures 


Are 

No.
Yes.
There is not enough information given to answer this question.
Yes.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal, and the measures of two angles. We know that 


Example Question #2 : How To Find If Right Triangles Are Congruent
Figures 


Are 

There is not enough information given to answer this question.
No.
Yes.
Yes.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of 


Example Question #491 : Triangles
Figures 


Are 

There is not enough information given to answer this question.
No.
Yes.
Yes.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of 
Simplify the ratio by dividing by
Thus, the corresponding sides are in the ratio 

All Basic Geometry Resources