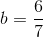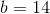Basic Arithmetic : Linear Equations with Whole Numbers
Study concepts, example questions & explanations for Basic Arithmetic
All Basic Arithmetic Resources
Example Questions
Example Question #1 : Linear Equations With Whole Numbers
Jimmy had 
Jimmy starts off with $60, and spends $3.50 everyday.
This means that he will have $56.50 after day 1, $53 after day 2, and so forth.
Only one equation satisfies this scenario. The rest are irrelevant.
Example Question #31 : Equations / Solution Sets
What is the solution of 
We add the two systems of equations:
For the Left Hand Side:
For the Right Hand Side:
So our resulting equation is:
Divide both sides by 10:
For the Left Hand Side:
For the Right Hand Side:
Our result is:
Example Question #32 : Whole Numbers
What is the solution of 
Reduce the second system by dividing by 3.
Second Equation:
Then we subtract the first equation from our new equation.
First Equation:
First Equation - Second Equation:
Left Hand Side:
Right Hand Side:
Our result is:
Example Question #2 : Linear Equations With Whole Numbers
What is the solution of 
We first add both systems of equations.
Left Hand Side:
Right Hand Side:
Our resulting equation is:
We divide both sides by 3.
Left Hand Side:
Right Hand Side:
Our resulting equation is:
Example Question #3 : Linear Equations With Whole Numbers
What is the solution of 
We first multiply the second equation by 4.
So our resulting equation is:
Then we subtract the first equation from the second new equation.
Left Hand Side:
Right Hand Side:
Resulting Equation:
We divide both sides by -15
Left Hand Side:
Right Hand Side:
Our result is:
Example Question #2 : Creating Equations With Whole Numbers
Dr. Jones charges a $50 flat fee for every patient. He also charges his patients $40 for every 10 minutes that he spends with him. If Mrs. Smith had an appointment that lasted 30 minutes, how much did she have to pay Dr. Jones?
$200
$120
$170
$90
$170
We can express Dr. Jones's rate in a linear equation:
Since Mrs. Smith's appointment lasted 30 minutes, we have 3 10-minute intervals. Then, we can plug in that number into our above equation to find out how much the appointment cost.
Example Question #1 : Whole And Part
Roman is ordering uniforms for the tennis team. He knows how many people are on the team and how many uniforms come in each box. Which equation can be used to solve for how many boxes 
b = number of students x number of uniforms per box
b = number of students ÷ number of uniforms per box
b = number of boxes x number of uniforms per box
b = number of boxes ÷ number of uniforms per box
b = number of students - number of uniforms per box
b = number of students ÷ number of uniforms per box
The total number of uniforms needed equals the number of students divided by the number of uniforms per box.
Example Question #1 : Linear Equations With Whole Numbers
Solve for 
First, add 6 to both sides so that the term with "x" is on its own.
Now, divide both sides by 2.
Example Question #2 : Linear Equations With Whole Numbers
Solve for 
Start by isolating the term with 
Divide both sides by 7.
Example Question #3 : Linear Equations With Whole Numbers
Solve for t.
First start by distributing the 7.
Now, add both sides by 14.
Finally, divide both sides by 7.
All Basic Arithmetic Resources
