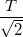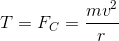Call Now to Set Up Tutoring:

(888) 888-0446

AP Physics C: Mechanics : AP Physics C

Study concepts, example questions & explanations for AP Physics C: Mechanics

Create An Account

All AP Physics C: Mechanics Resources

2 Diagnostic Tests 92 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #6 : Using Spring Equations

All angles in this problem are expressed in radians.

An object oscillates horizontally, and its displacement from equilibrium can be found using the equation:

$x=(2.00m)cos(\pi t+\frac{\pi }{2})$

where is in seconds. What is the velocity of the object at t=3.00s ?

Possible Answers:

$2.00\frac{m}{s}$

$-2\pi \frac{m}{s}$

$2\pi \frac{m}{s}$

$0.00\frac{m}{s}$

$\pi\frac{m}{s}$

Correct answer:

$2\pi \frac{m}{s}$

Explanation:

To find the equation for velocity, we take the first derivative of the position function. Don't forget the chain rule for the inside of the cosine!

$v=\frac{d(x)}{dt}$

$v=(-2.00\pi \frac{m}{s})sin(\pi t+\frac{\pi }{2})$

$v=(-2.00\pi \frac{m}{s})sin(\pi (2.00s))+\frac{\pi }{2})$

$v=2\pi \frac{m}{s}$

Report an Error

Example Question #41 : Mechanics Exam

A mass on the end of a spring oscillates back and forth. The period of an oscillating spring is measured to be 2.27 seconds. The mass is measured to be 0.300 kg. What is the spring's spring constant?

Possible Answers:

$0.422\frac{kg}{s^2}$

$1.07\frac{kg}{s^2}$

$0.873\frac{kg}{s^2}$

$0.575\frac{kg}{s^2}$

$0.943\frac{kg}{s^2}$

Correct answer:

$0.575\frac{kg}{s^2}$

Explanation:

To solve this problem, we can use the following equation:

$\small T=2\pi\sqrt{\frac{m}{k}}$

Here, is the period of an oscillation, is the mass of the oscillating thing in kg, and is the spring constant in $\frac{kg}{s^2}$ .

Rearranging the equation to solve for the spring constant, , we get:

$k\cdot =\frac{m}{(\frac{T}{2\pi})^2}$

Plugging in the two known values, we get:

$k\cdot =\frac{0.300kg}{(\frac{2.27s}{2\pi})^2}$

Solving for , we get $0.575\frac{kg}{s^2}$ .

Report an Error

Example Question #41 : Mechanics Exam

A $1.5\: kg$ block on a frictionless table is connected to a horizontal spring with constant $450\: N/m$ . If the block is released from rest when the spring is stretched a distance of $7\: cm$ ,

what is its speed when the spring is compressed a distance of $3\: cm$ ?

Possible Answers:

$1.32\:m/s$

$1.2\:m/s$

$1.1\:m/s$

$0.849\:m/s$

$0.995\:m/s$

Correct answer:

$1.1\:m/s$

Explanation:

Assuming this is a frictionless table, we don't have to take the work done by friction into account.

This is a conservation of energy problem. In this problem we have to realize that the potential energy of the spring at $7\:cm$ is equal to the kinetic energy of the spring at $3\:cm$ + the potential energy of the spring at $3\:cm$ .

This can be shown in the following equation:

$\frac{1}{2}kx_7^2 = \frac{1}{2}mv^2 + \frac{1}{2}kx_3^2$

If we solve for , we get the following equation:

$v = \sqrt{2\cdot\frac{\frac{1}{2}kx_7^2-\frac{1}{2}kx_3^2}{m}}$

Remember to convert the distances given in centimeters to meters.

If we plug in all the variables, we get $v = 1.1\:m/s$

Report an Error

Example Question #41 : Ap Physics C

A simple pendulum of length swings at a radius from a fixed point on the ceiling. As it moves, the pendulum creates an angle $\theta$ with the line that extends vertically downwards from the fixed point. At what angle does the mass attached to the pendulum have the highest kinetic energy?

Possible Answers:

${30^\circ}$

$90^\circ$

$0^\circ$

$45^\circ$

Correct answer:

$0^\circ$

Explanation:

The correct answer is $0^\circ$ . Since the pendulum is at the bottom of its motion at this point, it has the lowest amount of energy given to gravitational potential and thus, the highest kinetic energy.

Report an Error

Example Question #41 : Motion

If a simple pendulum is constructed using a rope of negligible weight and a large steel ball weighing 100N . What is the period of the pendulum?

Possible Answers:

$2\pi\cdot\sqrt{10}s$

Not enough information

$2\pi s$

200s

2 s

Correct answer:

2 s

Explanation:

Use the equation for the period of a simple pendulum:

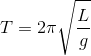
$T=2\pi\sqrt\frac{L}{g}$

Here, 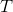is the period in seconds, is the length of the pendulum in meters, and is the acceleration due to gravity in $\frac{m}{s^2}$ .

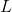
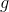
We can plug in the given quantities for length and acceleration to solve for the period.

$T=2\pi\sqrt\frac{1}{9.8}\approx2s$

Note that the mass of the rope as negligible. We also need not incorporate the extraneous information regarding the weight of the steel ball attached to the pendulum. This does not influence the period of this simple pendulum.

Report an Error

Example Question #11 : Harmonic Motion

Two springs big

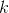
A block of mass $\small m$ is attached to two springs, each of whose spring constant is $\small k$ . The ends of the springs are fixed, and the block is free to move back and forth. It is released from rest at an initial amplitude, and its period is measured to be $\small T$ . What would the period be if the spring on the right side were to be moved to the other side, attached along side of the other spring?

Possible Answers:

$\small \frac{T}{2}$

$\small 2T$

$\small \frac{T}{\sqrt{2}}$

$\small T$

$T\sqrt{2}$

Correct answer:

$\small T$

Explanation:

Because the springs are effectively in a parallel arrangement already, moving one does not change the effective spring constant, and therefore does not affect the period.

Report an Error

Example Question #1 : Circular And Rotational Motion

Rotatingball

A ball of mass is tied to a rope and moves along a horizontal circular path of radius as shown in the diagram (view from above). The maximum tension the rope can stand before breaking is given by $T_{max}$ . Which of the following represents the ball's linear velocity given that the rope does not break?

Possible Answers:

$v\geq\sqrt{rT_{max}}$

$v\geq\sqrt{\frac{rT_{max}}{m}}$

$v\leq\sqrt{\frac{rT_{max}}{m}}$

$v\leq\sqrt{rT_{max}}$

None of these

Correct answer:

$v\leq\sqrt{\frac{rT_{max}}{m}}$

Explanation:

This is a centripetal force problem. In this case the tension on the rope is the centripetal force that keeps the ball moving on a circle.

$T=F_C=\frac{mv^2}{r}$

If we want for the rope not to break, then the tension should never exceed $T_{max}$ .

$T_{max}\geq\frac{mv^2}{r}$

Now we just solve for velocity:

$v\leq\sqrt{\frac{rT_{max}}{m}}}$

Report an Error

Example Question #1 : Rotational Motion And Torque

What is the rotational equivalent of mass?

Possible Answers:

Angular momentum

Torque

Radius

Moment of inertia

Correct answer:

Moment of inertia

Explanation:

The correct answer is moment of inertia. For linear equations, mass is what resists force and causes lower linear accelerations. Similarly, in rotational equations, moment of inertia resists torque and causes lower angular accelerations.

Report an Error

Example Question #2 : Rotational Motion And Torque

In rotational kinematics equations, what quantity is analogous to force in linear kinematics equations?

Possible Answers:

Angular acceleration

Torque

Moment of inertia

Impulse

Correct answer:

Torque

Explanation:

Just as force causes linear acceleration, torque causes angular acceleration. This can be seen most in the linear-rotational comparison of Newton's second law:

F=ma

$\tau=I\alpha$

Report an Error

Example Question #1 : Understanding Linear Rotational Equivalents

A boot is put in a 1 m stick which is attached to a rotor. The rotor turns with an angular velocity of $30\pi \frac{rad}{s}$ . What is the linear velocity of the boot?

Possible Answers:

$15\frac{m}{s}$

$15\pi\frac{m}{s}$

$30\frac{m}{s}$

$30\pi\frac{m}{s}$

$3\pi\frac{m}{s}$

Correct answer:

$30\pi\frac{m}{s}$

Explanation:

Linear (tangential) velocity, $v_{T}$ is given by the following equation:

$v_{T}=\omega r$

Here, $\omega$ is the angular velocity in radians per second and is the radius in meters.

r=1m

Solve.

$\omega = 30\pi \frac{rad}{s}$

$\omega = 30\pi\frac{m}{s}$

Report an Error

View Tutors

Donald
Certified Tutor

Cleveland State University, Bachelor of Science, Chemistry. University of Southern California, Doctor of Philosophy, Organic ...

View Tutors

Victoria
Certified Tutor

Norte Dame de Namur University, Bachelor in Arts, Sociology. University of San Francisco, Master of Arts, Organizational Lead...

View Tutors

Shweta
Certified Tutor

All India Management Association , Master's/Graduate, Human Resource Management . Indian Law Institute , Master's/Graduate, C...

All AP Physics C: Mechanics Resources

2 Diagnostic Tests 92 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Houston, Calculus Tutors in Houston, Algebra Tutors in Boston, GMAT Tutors in New York City, English Tutors in Miami, Chemistry Tutors in Philadelphia, SAT Tutors in Atlanta, ISEE Tutors in Dallas Fort Worth, English Tutors in Seattle, Computer Science Tutors in Miami

Popular Courses & Classes

SAT Courses & Classes in Seattle, LSAT Courses & Classes in New York City, ACT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Atlanta, GRE Courses & Classes in Seattle, GMAT Courses & Classes in Miami, SSAT Courses & Classes in Miami, LSAT Courses & Classes in Atlanta

Popular Test Prep

ISEE Test Prep in Chicago, LSAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Miami, ISEE Test Prep in Boston, SSAT Test Prep in Philadelphia, MCAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Phoenix, MCAT Test Prep in Denver, SSAT Test Prep in Dallas Fort Worth, GMAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Physics C: Mechanics : AP Physics C

Study concepts, example questions & explanations for AP Physics C: Mechanics

All AP Physics C: Mechanics Resources

Example Questions

Example Question #6 : Using Spring Equations

Example Question #41 : Mechanics Exam

Example Question #41 : Mechanics Exam

Example Question #41 : Ap Physics C

Example Question #41 : Motion

Example Question #11 : Harmonic Motion

Example Question #1 : Circular And Rotational Motion

Example Question #1 : Rotational Motion And Torque

Example Question #2 : Rotational Motion And Torque

Example Question #1 : Understanding Linear Rotational Equivalents

All AP Physics C: Mechanics Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: