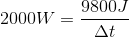Since the man's kinetic energy remains constant, we are really solving for the rate at which he gains potential energy.

\(\displaystyle U = mgh\)

However, when we find the change of this with respect to time (aka power), the expression becomes:

\(\displaystyle P = \frac{\Delta U}{t}=\frac{mg\Delta h}{t}\)

We can calculate the change in height by using the velocity of the man and the slope of the hill:

\(\displaystyle \frac{\Delta h}{t} = v_y = v\cdot sin(30^{\circ})\)

Substituting this into the equation for power, we get:

\(\displaystyle P = m\cdot g \cdot v\cdot sin(30^{\circ})\)

We know all of these values, so we can plug in and solve:

\(\displaystyle P = (55)(10)(2)sin(30^{\circ}) = 550 W\)

We can use the work-energy theorem to solve this problem, which says the the net work done is equal to the change in kinetic energy:

\(\displaystyle W_{net} = \Delta K\)

We can expand this to write:

\(\displaystyle W_{net} = \frac{1}{2}m(v_f^2-v_i^2)\)

We know that the elevator was initially at a standstill, so the equation becomes:

\(\displaystyle W_{net} = \frac{1}{2}mv_f^2\)

We are given the mass of the elevator plus passengers, as well as the final velocity, so we can simply solve:

\(\displaystyle m=1000+5(80)=1400kg\)

\(\displaystyle W_{net} = \frac{1}{2}(1400kg)(3\frac{m}{s})^2 = 6300J\)

Since the diver is at terminal velocity, we know that the force exerted by the air is equal to the gravitational force. Let's calculate that first:

\(\displaystyle F = mg = 50kg\cdot 10\frac{m}{s^2} = 500 N\)

Now that we know the force exerted by the wind, we have to connect the dots to turn this into units of power. We can do this by using the velocity of the man. Power is simply work done over time. We aren't given a time frame in the problem statement, so let's just choose a time frame of 1 second to keep things simple. Over 1 second, we know that the diver falls 75 meters. From this, we can calculate how much gravitational potential energy is lost over this distance:

\(\displaystyle \Delta U = mg\Delta h = 500N \cdot 75 m = 37500 J\)

This means that 37500J were exerted by the wind over a period of 1 second. Now we can simply use the formula for power:

\(\displaystyle P = \frac{W}{t} = \frac{37500 J}{1s} = 37500 W = 37.5 kW\)

This problem emphasizes a great tactic in solving most physics problems. If you ever get stuck, simply follow your units. See what units you have, what units you can work with, and try to figure out a logical path that combines them to get to the units that your answer should be. Although this is NOT how you should go about physics, it is a good tactic to use when you can't simply work through the problem with the concepts you have been taught.

We first need to know the frictional force between the crate and floor:

\(\displaystyle F_f = \mu_k N = (0.2)(10\frac{m}{s^2})(20kg) = 40N\)

Now that we have the frictional force, we can simply multiply it by the velocity of the crate to find power:

\(\displaystyle P = F_fv = (40N)(1.5\frac{m}{s}) = 60W\)

First we find the total work required to lift the crate:

\(\displaystyle W=\Delta PE=mg\Delta h\)

We are given the mass, change in height, and the acceleration of gravity. Using these values, we can solve for the total work done.

\(\displaystyle W=(100kg)(9.8\frac{m}{s^2})(10m)=9800J\)

Next, we can use the equation for power to find the time to complete this task if the engine is working at its maximum power.

\(\displaystyle P=\frac{\Delta W}{\Delta t}\)

\(\displaystyle 2000W=\frac{9800J}{\Delta t}\)

\(\displaystyle \Delta t=\frac{9800J}{2000W}=4.9s\)

We can use the equation for conservation of energy to solve for the work done by the water on the diver:

\(\displaystyle E= U_i+K_i=U_f+K_f+ W\)

We can eliminate both kinetic energies since the diver is stationary at the initial and final states. If we assume a final height of \(\displaystyle 0m\), we can also eliminate final potential energy. Keep in mind that this assumption requires that we add the distances above and below the water, making our total height 21m. Substituting in our expresssion for initial potential energy, we get:

\(\displaystyle W = mgh_i = (70kg)(10\frac{m}{s^2})(21m)\)

\(\displaystyle W = 14.7kJ\)

That is the work done on the diver. Since we know the time period during which this work is done, we can calculate the average power of the water on the diver:

\(\displaystyle P = \frac{W}{t}=\frac{14.7kJ}{0.4s}=36.8kW\)

We are given the mass of the car, its initial velocity, its final velocity, and the amount of time needed to reach its final velocity. We are then asked to calculate the power involved in the overall process. We can first start by noting that power is equal to work divided by time:

\(\displaystyle P=\frac{W}{t}\)

Since we are given the amount of time \(\displaystyle t\) in the question stem, we'll need to find a way to calculate \(\displaystyle W\). To do so, we can relate the work done by the change in the kinetic energy of the car.

\(\displaystyle W=\Delta KE=KE_{f}-KE_{i}\)

Since we're given mass, final velocity, and initial velocity, we can use these values to calculate the change in kinetic energy.

\(\displaystyle W=\frac{1}{2}mv_{f}^{2}-\frac{1}{2}mv_{i}^{2}\)

Furthermore, since the car is starting from rest, its initial velocity is equal to zero. Thus, the initial kinetic energy is equal to zero, meaning that the work done is equal to the final kinetic energy.

\(\displaystyle W=\frac{1}{2}mv_{f}^{2}\)

Substitute into the the equation for power and solve.

\(\displaystyle W=\frac{\frac{1}{2}mv_{f}^{2}}{t}\)

\(\displaystyle W=\frac{mv_{f}^{2}}{2t}=\frac{(1000 kg)(50\frac{m}{s})^{2}}{2(7.5 s)}=166666.667W=167kW\)

Power is most basically put as the change in energy over time. 

\(\displaystyle P=\frac{\Delta E}{t}\)

For this problem, the only energy change we are able to consider is the change in gravititational potential energy. We are told the speed does not change so the kinetic energy is constant. The power output of the wench is going only into bringing the box higher in the gravitiational field. We ignore friction for this problem. So, rewriting the first equation:

\(\displaystyle P=\frac{\Delta GPE}{t}\)

\(\displaystyle P=\frac{(mgh)_{f}-(mgh)_{i}}{t}\)

We have the liberty to set the initial height to zero and then guage the final height starting from zero. This eliminates the initial term. 

\(\displaystyle P=\frac{(mgh)_{f}}{t}\)

We are given the mass and time, but we need to use trig to solve for the height. We can solve for the height of the ramp using sin.

\(\displaystyle O\) is for the opposite side of the triangle and H is the hypotenuse, not to get confused with h. The opposite side of the triangle is our height h.

\(\displaystyle \sin(\Theta )=O/H\)

So, \(\displaystyle H\sin (\Theta )=O\)

Rewriting h in our power equation:

\(\displaystyle P=\frac{(mgH\sin (\Theta ))_}{t}\)

Plugging into this equation we get

 \(\displaystyle 6.1\: \textup{Watts}\).

Firstly, remember that the only force in play here is gravity. Since gravity is a conservative force, to move up \(\displaystyle 7m\), it's going to require work equal to:

\(\displaystyle W=mg\Delta h\), where \(\displaystyle m\) is the mass of the object, \(\displaystyle g\) is the gravitational constant, and \(\displaystyle \Delta h\) is the change in distance from the ground. Since we are moving the object up by \(\displaystyle 7m\), \(\displaystyle \Delta h=7m\)

In our problem, \(\displaystyle m=12kg\) and \(\displaystyle g=9.8\frac{m}{s^2}\)

Work required to move up an object is going to be:

\(\displaystyle W=12kg\cdot9.8\frac{m}{s^2}\cdot7m= 820J\)

The equation for power is given by:

\(\displaystyle P=\frac{W}{t}\)

Where \(\displaystyle P\) is power, \(\displaystyle W\) is work and \(\displaystyle t\) is time.

However, this equation can be simplified even further:

\(\displaystyle P = \frac{F*d}{t}\)

Since we know that Force is equal to the mass times the acceleration (due to gravity in this scenario):

\(\displaystyle P = \frac{m*a*d}{t}\)

Here we can substitute our known values and solve for power.

\(\displaystyle P = \frac{(50kg)(10\frac{m}{s^2})(10m)}{100sec}= 50W\)