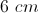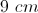Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Isosceles Triangles

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find The Length Of The Side Of Of An Acute / Obtuse Isosceles Triangle

In the standard (x,y) coordinate plane, the points (1,-1) and (1,7) form two vertices of an isosceles triangle. Which of the following points could be the third vertex?

Possible Answers:

(2,3)

(0,0)

(4,5)

(3,4)

(2,4)

Correct answer:

(2,3)

Explanation:

To form an isosceles triangle here, we need to create a third vertex whose coordinate is between and . If a vertex is placed at (2,3) , the distance from (1,-1) to this point will be $\sqrt{17}$ . The distance from (1,7) to this point will be the same.

Report an Error

Example Question #175 : Triangles

Screen_shot_2015-05-07_at_4.37.54_pm

Note: Figure is not drawn to scale.

In the figure above, points A, B, C are collinear and $\angle$ ABE is a right angle. If $\overline{BD}=\overline{DE}$ and $\measuredangle$ BDE is $58^{\circ}$ , what is $\measuredangle CBD$ ?

Possible Answers:

$29^{\circ}$

$30^{\circ}$

$61^{\circ}$

$122^{\circ}$

$35^{\circ}$

Correct answer:

$29^{\circ}$

Explanation:

Because $\bigtriangleup BDE$ is isosceles, $\measuredangle DBE$ equals $\left(\frac{180-58}{2}\right)^{\circ}$ or $61^{\circ}$ .

We know that $\measuredangle ABE, \measuredangle DBE, \measuredangle CBD$ add up to $180^{\circ}$ , so $\measuredangle CBD$ must equal $(180-90-61)^{\circ}$ or $29^{\circ}$ .

Report an Error

Example Question #231 : Act Math

A light beam of pure white light is aimed horizontally at a prism, which splits the light into two streams that diverge at a $30^{\circ}$ angle. The split beams each travel exactly $\textup{5 feet}$ from the prism before striking two optic sensors (one for each beam).

What is the distance, in feet, between the two sensors?

Round your final answer to the nearest tenth. Do not round until then.

Possible Answers:

7.3

7.7

2.9

2.6

2.1

Correct answer:

2.6

Explanation:

This problem can be solved when one realizes that the light beam's split has resulted in an acute isosceles triangle. The triangle as stated has two sides of feet apiece, which meets the requirement for isosceles triangles, and having one angle of $30^{\circ}$ at the vertex where the two congruent sides meet means the other two angles must be $75^{\circ}$ and $75^{\circ}$ . The missing side connecting the two sensors, therefore, is opposite the $30^{\circ}$ angle.

Since we know at least two angles and at least one side of our triangle, we can use the Law of Sines to calculate the remainder. The Law of Sines says that for any triangle with angles A, B and and opposite sides a, b and :

$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$ .

Plugging in one of our $75^{\circ}$ angles (and its corresponding ft side) into this equation, as well as our $30^{\circ}$ angle (and its corresponding unknown side) into this equation gives us:

$\frac{\sin 75^{\circ}}{5} = \frac{ \sin 30^{\circ}}{x}$

Next, cross-multiply:

$\frac{\sin 75^{\circ}}{5} = \frac{\sin 30^{\circ}}{x}$ ---> $x\sin 75^{\circ} = 5\sin 30^{\circ}$

Now simplify and solve:

$x = \frac{5\sin 30^{\circ}}{\sin 75^{\circ}} = 2.588$

Rounding, we see our missing side is $2.65\textup{ feet}$ long.

Report an Error

Example Question #1 : Isosceles Triangles

An isosceles triangle has a base of $12\ cm$ and an area of $42\ cm^{2}$ . What must be the height of this triangle?

Possible Answers:

$7\ cm$

$8\ cm$

$6\ cm$

$9\ cm$

$10\ cm$

Correct answer:

$7\ cm$

Explanation:

$A=\frac{1}{2}bh$ .

$6x=42$

$x=7$

Report an Error

Example Question #171 : Triangles

What is the height of an isosceles triangle which has a base of 4cm and an area of 24cm^2 ?

Possible Answers:

8cm

24cm

6cm

16cm

12cm

Correct answer:

12cm

Explanation:

The area of a triangle is given by the equation:

$\small A=\frac{1}{2}bh$

In this case, we are given the area ( $\small A$ ) and the base ( $\small b$ ) and are asked to solve for height ( $\small h$ ).

To do this, we must plug in the given values for $\small A$ and $\small b$ , which gives the following:

$\small 24\;cm^2=\frac{1}{2}(4\; cm)h$

We then must multiply the right side, and then divide the entire equation by 2, in order to solve for $\small h$ :

$\small 24\;cm^2=2\;cm(h)$

$\small \frac{24\; cm^2}{2\; cm}=\frac{2\; cm(h)}{2\; cm}$

$\small 12\;cm=h$

$\small h=12\;cm$

Therefore, the height of the triangle is $\small 12\;cm$ .

Report an Error

Example Question #175 : Triangles

There are two obtuse triangles. The obtuse angle of triangle one is $101^{\circ}$ . The sum of two angles in the second triangle is $80^{\circ}$ . When are these two triangles congruent?

Possible Answers:

Cannot be determined

The two triangles cannot be congruent

The two triangles must be congruent

When the obtuse angle is congruent to the smallest angle of the other triangle

When the sum of angle A and angle B in triangle 1 is equal to the sum of the corresponding angles in triangle 2

Correct answer:

The two triangles cannot be congruent

Explanation:

In order for two obtuse triangles to be congruent, the sum of the two smaller angles must equal the sum of the two smaller angles of the second triangle. That is, excluding the obtuse angle.

The first triangle has an obtuse angle of $101^{\circ}$ . That means the sum of the other two angles is $79^{\circ}$ . The sum of the corresponding angles in triangle 2 is $80^{\circ}$ . Therefore, because $79^{\circ}$ is not equal to $80^{\circ}$ , the two obtuse triangles cannot be congruent.

Report an Error

View ACT Math Tutors

Nate
Certified Tutor

University of Wisconsin-Oshkosh, non degree, Prepharmacy. University of Wisconsin-Madison, Pharmaceutical Chemist, Pharmacy.

View ACT Math Tutors

Sumit
Certified Tutor

Calcutta University, Bachelor of Science, Mathematics. Indian Statistical Institute, Master of Science, Mathematics.

View ACT Math Tutors

Jason
Certified Tutor

Brigham Young University, Bachelor, Neuroscience.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Seattle, LSAT Courses & Classes in San Diego, LSAT Courses & Classes in Washington DC, Spanish Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in New York City, SAT Courses & Classes in Washington DC, SSAT Courses & Classes in Chicago, MCAT Courses & Classes in Los Angeles, GRE Courses & Classes in Dallas Fort Worth

Popular Test Prep

MCAT Test Prep in Houston, GRE Test Prep in Denver, MCAT Test Prep in San Diego, SSAT Test Prep in Miami, SSAT Test Prep in Dallas Fort Worth, GRE Test Prep in Los Angeles, SSAT Test Prep in Houston, LSAT Test Prep in Miami, SAT Test Prep in Chicago, ACT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Isosceles Triangles

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #2 : How To Find The Length Of The Side Of Of An Acute / Obtuse Isosceles Triangle

Example Question #175 : Triangles

Example Question #231 : Act Math

Example Question #1 : Isosceles Triangles

Example Question #171 : Triangles

Example Question #175 : Triangles

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: