All ACT Math Resources
Example Questions
Example Question #411 : Plane Geometry
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
6√2
10√2
15
11
2√5
10√2
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c
Example Question #261 : Triangles
Jim leaves his home and walks 10 minutes due west and 5 minutes due south. If Jim could walk a straight line from his current position back to his house, how far, in minutes, is Jim from home?
√10
√5
5√5
6√6
5√5
By using Pythagorean Theorem, we can solve for the distance “as the crow flies” from Jim to his home:
102 + 52 = x2
100 + 25 = x2
√125 = x, but we still need to factor the square root
√125 = √25*5, and since the √25 = 5, we can move that outside of the radical, so
5√5= x
Example Question #142 : Triangles
A square enclosure has a total area of 3,600 square feet. What is the length, in feet, of a diagonal across the field rounded to the nearest whole number?
95
60
100
75
85
85
In order to find the length of the diagonal accross a square, we must first find the lengths of the individual sides.
The area of a square is found by multiply the lengths of 2 sides of a square by itself.
So, the square root of 3,600 comes out to 60 ft.
The diagonal of a square can be found by treating it like a right triangle, and so, we can use the pythagorean theorem for a right triangle.
602 + 602 = C2
the square root of 7,200 is 84.8, which can be rounded to 85
Example Question #172 : Plane Geometry
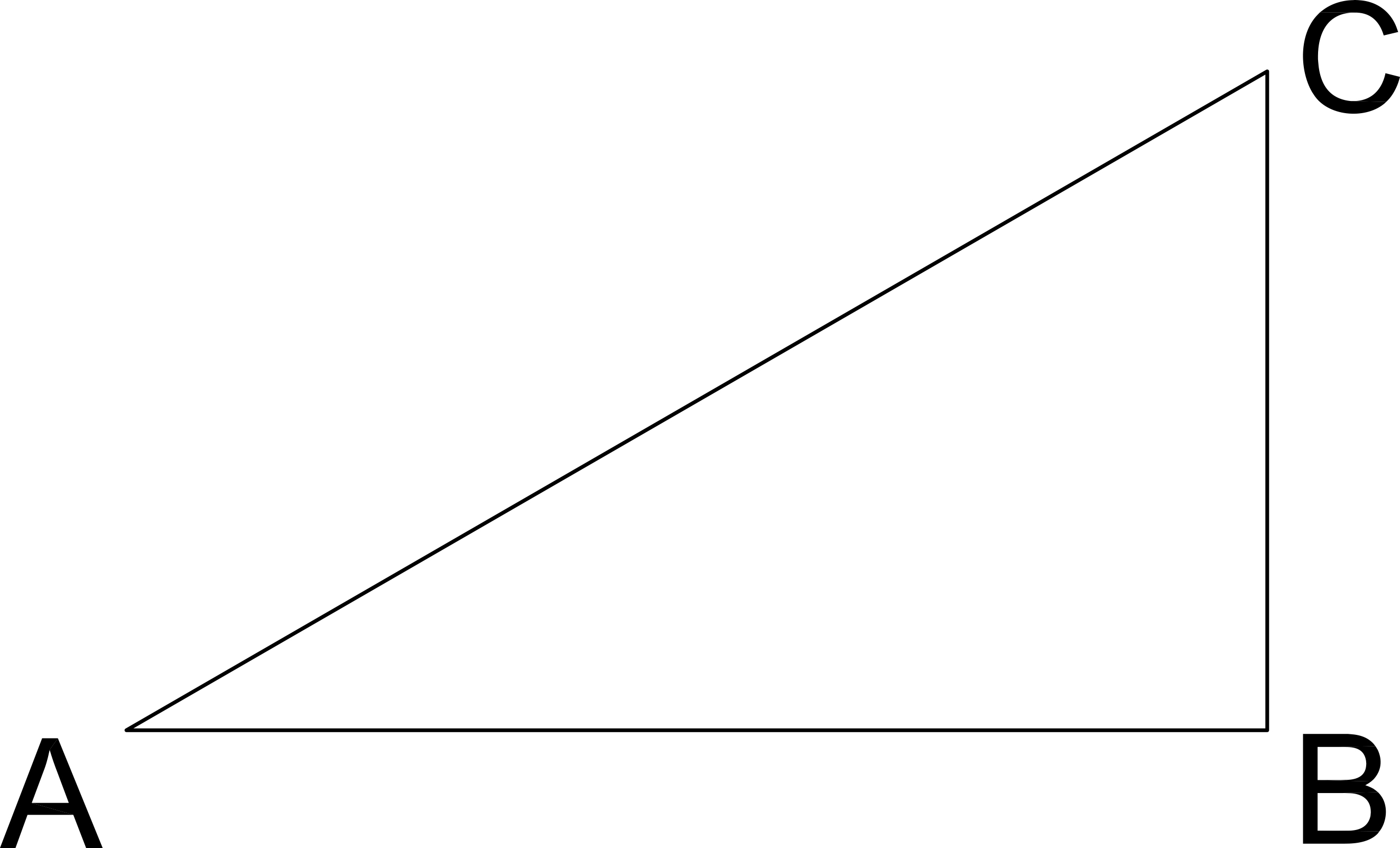
If the length of CB is 6 and the angle C measures 45º, what is the length of AC in the given right triangle?
12√2
6
6√2
9
72
6√2
Pythagorean Theorum
AB2 + BC2 = AC2
If C is 45º then A is 45º, therefore AB = BC
AB2 + BC2 = AC2
62 + 62 = AC2
2*62 = AC2
AC = √(2*62) = 6√2
Example Question #61 : Triangles
You leave on a road trip driving due North from Savannah, Georgia, at 8am. You drive for 5 hours at 60mph and then head due East for 2 hours at 50mph. After those 7 hours, how far are you Northeast from Savannah as the crow flies (in miles)?
Distance = hours * mph
North Distance = 5 hours * 60 mph = 300 miles
East Distance = 2 hours * 50 mph = 100 miles
Use Pythagorean Theorem to determine Northeast Distance
3002 + 1002 =NE2
90000 + 10000 = 100000 = NE2
NE = √100000
Example Question #51 : Right Triangles
A square garden has an area of 49 ft2. To the nearest foot, what is the diagonal distance across the garden?
10
8
9
7
11
10
Since the garden is square, the two sides are equal to the square root of the area, making each side 7 feet. Then, using the Pythagorean Theorem, set up the equation 72 + 72 = the length of the diagonal squared. The length of the diagonal is the square root of 98, which is closest to 10.
Example Question #62 : Triangles
A man at the top of a lighthouse is watching birds through a telescope. He spots a pelican 5 miles due north of the lighthouse. The pelican flies due west for 12 miles before resting on a buoy. What is the distance, in miles, from the pelican's current resting spot to the lighthouse?
We look at the 3 points of interest: the lighthouse, where the pelican started, and where the pelican ended. We can see that if we connect these 3 points with lines, they form a right triangle. (From due north, flying exactly west creates a 90 degree angle.) The three sides of the triangle are 5 miles, 13 miles and an unknown distance. Using the Pythagorean Theorem we get:
Example Question #181 : Plane Geometry
An airplane is 8 miles west and 15 miles south of its destination. Approximately how far is the plane from its destination, in miles?
A right triangle can be drawn between the airplane and its destination.
Destination
15 miles  Airplane
Airplane
8 miles
We can solve for the hypotenuse, x, of the triangle:
82 + 152 = x2
64 + 225 = x2
289 = x2
x = 17 miles
Example Question #421 : Plane Geometry
An 8-foot-tall tree is perpendicular to the ground and casts a 6-foot shadow. What is the distance, to the nearest foot, from the top of the tree to the end of the shadow?
In order to find the distance from the top of the tree to the end of the shadow, draw a right triangle with the height(tree) labeled as 8 and base(shadow) labeled as 6:

From this diagram, you can see that the distance being asked for is the hypotenuse. From here, you can either use the Pythagorean Theorem:

or you can notice that this is simililar to a 3-4-5 triangle. Since the lengths are just increased by a factor of 2, the hypotenuse that is normally 5 would be 10.
Example Question #111 : Plane Geometry

In the figure above, 



Assigning the length of ED the value of x, the value of AE will be 3x. That makes the entire side AD equal to 4x. Since the figure is a square, all four sides will be equal to 4x. Also, since the figure is a square, then angle A of triangle ABE is a right angle. That gives triangle ABE sides of 3x, 4x and 10. Using the Pythagorean theorem:
(3x)2 + (4x)2 = 102
9x2 + 16x2 = 100
25x2 = 100
x2 = 4
x = 2
With x = 2, each side of the square is 4x, or 8. The area of a square is length times width. In this case, that's 8 * 8, which is 64.
Certified Tutor
Certified Tutor
All ACT Math Resources




































