All 7th Grade Math Resources
Example Questions
Example Question #1 : Number Sense
A sweater was originally 

In order to solve this problem, we need to calculate 

We can convert a percent into a decimal by moving the decimal two places to the left:
Next, we can multiply:
Remember, we are taking 
Example Question #2 : Number Sense
The rectangle provided is a scaled drawing of a rectangular yard. Given the scale of 

This question is asking us to solve for the actual size of the length of the rectangle, therefore, we first need to recall which side is considered to be the length of the rectangle.

In this example, the length of the rectangle is 

Next, we cross multiply and solve for 
Example Question #1 : Algebra
Billy makes 


We know that Billy needs to make more than 
Also, since Billy will make 


So far we have the following:
Next, we know that he makes 
This means we need to add the 
When we put all of these pieces together, we will get the following inequality:
Example Question #1 : Operations
Andrew spends every Saturday at the gym working out. He can complete 

The phrase "per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have the portion of his workout, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
Andrew can complete 
Example Question #2 : Operations
Solve:
In order to solve this problem, we need to start at 

Next, we have 




The orange arrow moved 

Example Question #3 : Operations
Solve:
We know the following information:
In this particular case, do the negative numbers change our answer? . There are a couple of rules that we need to remember when multiplying with negative numbers:
- A negative number divided by a positive number will always equal a negative number, and a positive number divided by a negative number will always equal a negative number.
- A negative number divided by a negative number will always equal a positive number
Thus,
Example Question #1 : Geometry
If a rectangle possesses a width of 

In order to solve this problem, we need to recall the formula for perimeter of a rectangle:
We can substitute in our known values and solve for our unknown variable (i.e. length):
We want to isolate the 

Next, we can divide each side by
The length of the rectangle is
Example Question #1 : Geometry
The figure represents a set of supplementary angles, solve for 

Supplementary angles are defined as two angles that when added together equal
From the question, we know that the two angles are supplementary, and thus equal 
Next we can solve for 
Example Question #2 : Geometry
What is the area of the circle provided?
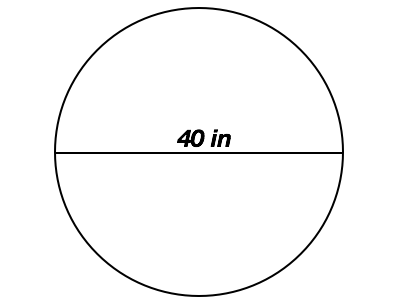
In order to solve this problem, we need to recall the formula for the area of a circle:
The circle in this question provides us with the diameter, so we first have to solve for the radius. Remember, the radius is half the diameter:
Now that we have the radius we can use the formula to solve:
Solve:
Example Question #3 : Geometry

What is the area of the triangle pictured above?
40
60
30
12
24
24
The area of a triangle is calculated using the formula 

All 7th Grade Math Resources






![\frac{\begin{array}[b]{r}15\\ \times\ .15\end{array}}{ \ \ \ \space 2.25}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912360/gif.latex)
![\frac{\begin{array}[b]{r}15.00\\ -\ 2.25\end{array}}{ \ \ \space 12.75}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/912361/gif.latex)








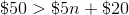

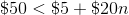


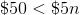





























![\frac{\begin{array}[b]{r}18=2l+4\\ -4\ \ \ \ \ \ -4\end{array}}{\\\\14=2l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924412/gif.latex)

![\frac{\begin{array}[b]{r}\frac{14}{2}=\frac{2l}{2}\\\end{array}}{7=l}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/924413/gif.latex)






![\frac{\begin{array}[b]{r}x+99=180\\ -99\ \ -99\end{array}}{x= 81}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/931827/gif.latex)













