GRE Math : How to find the area of a sector
Study concepts, example questions & explanations for GRE Math
All GRE Math Resources
Example Questions
Example Question #1 : How To Find The Area Of A Sector
If the outer arc of 1/12th of a circular pie is 7π, what is the area of 1/4th of the pie?
21π
441π
10.5π
1764π
None of the other answers
441π
Our initial data tells us that (1/12)c = 7π or (1/12)πd = 7π. This simplifies to (1/12)d = 7 or d = 84. Furthermore, we know that r is 42. Given this, we can ascertain the area of a quarter of the whole pie by taking one fourth of the whole area or 0.25 * π * 422 = 0.25 * 1764 * π = 441π
Example Question #1 : How To Find The Area Of A Sector
What is the area of a sector of a circle of radius 4 that spans an arc of 86 degrees?
1/4 * ∏
172/45 * ∏
17/42 * ∏
12/53 * ∏
1/5 * ∏
172/45 * ∏
sector area = ∏ * r2 * degrees/360 = ∏ * 42 * 86/360 = 172/45 * ∏
Example Question #1 : How To Find The Area Of A Sector
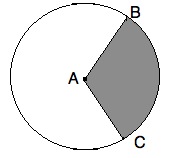
The circle above has a center of A, and points B and C lie on the circumference.
What is the area of the shaded region?
None of the other answers
We need to begin by finding the area of the following sector:
If ∠BAC = 120°, then the area of sector BAC is equal to 120 / 360 = 1/3 of the entire circle. Since AC is 12 and is a radius, we know the total area is pi *122 = 144*pi. The sector is then 144*pi / 3 = 48*pi.
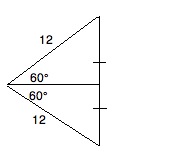
Now, we need to find the area of the triangle ABC. Since AB and AC are equal (both being radii of our circle), we have an icoseles triangle. If we drop a height from ∠BAC, we have the following triangle ABC:
We can use the 30-60-90 rule to find the height and base. One half of the base (x) is found by the following ratio:
√(3) / 2 = x / 12
Solving for x, we get: x = 6 * √(3). Therefore, the base is 12 * √(3).
To find the height (y), we use the following ratio:
1 / 2 = y / 12
Solving for y, we get y = 6.
Therefore, the area of the triangle = 0.5 * 6 * 12 * √(3) = 3 * 12 * √(3) = 36 * √(3)
The area of the shaded region is then 48*pi - 36 * √(3).
All GRE Math Resources
