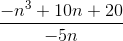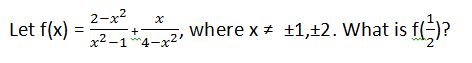GRE Math : Rational Expressions

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Subtract Rational Expressions With Different Denominators

Choose the answer which best simplifies the following expression:

$\frac{2n + 4}{n} - \frac{n^2}{5}$

Possible Answers:

$\frac{-n^3+10n+20}{-5n}$

$\frac{n^3+10n+20}{5n}$

$\frac{-n^2+10n+20}{5n}$

$\frac{-n^3+10n+20}{5n}$

$\frac{-n^3-10n-20}{5n}$

Correct answer:

$\frac{-n^3+10n+20}{5n}$

Explanation:

To simplify this problem, multiply each term by the denominator of the other over itself:

$\frac{2n + 4}{n}\left(\frac{5}{5}\right) - \frac{n^2}{5}\left(\frac{n}{n}\right)$

$\frac{10n + 20}{5n} - \frac{n^3}{5n}$

Now that both terms share a denominator, you can subtract:

$\frac{-n^3+10n+20}{5n}$

Report an Error

Example Question #2 : How To Subtract Rational Expressions With Different Denominators

Choose the answer which best simplifies the following expression:

$\frac{2x + a}{4} - \frac{3}{2a}$

Possible Answers:

$\frac{2ax + a^2 - 6}{4a^2}$

$\frac{4ax + 2a^2 - 12}{8a}$

$\frac{2ax + a^2 - 6}{4a}$

$\frac{2ax + a^2 - 6x}{4a}$

$\frac{2a^2x + a^2 - 6}{4a}$

Correct answer:

$\frac{2ax + a^2 - 6}{4a}$

Explanation:

To solve this problem, first multiply each term of the original expression by the denomenator of the other over itself:

$\frac{2x + a}{4}(\frac{2a}{2a}) - \frac{3}{2a}(\frac{4}{4})$

Then you will have two terms with a common denomenator:

$\frac{4ax + 2a^2}{8a} - \frac{12}{8a}$

Combine the terms and simplify for your final answer:

$\frac{4ax +2a^2 - 12}{8a}$

$\frac{2ax + a^2 - 6}{4a}$

Report an Error

Example Question #12 : Rational Expressions

Choose the answer which best simplifies the expression below:

$\frac{2p^2 - 3p}{b} - \frac{b^2}{p}$

Possible Answers:

$\frac{2p^3 - 3p^2 -b^3}{b}$

$\frac{2p^3 - 3p^2 -b^3}{pb}$

$\frac{2p - 3p^2 -b^3}{pb}$

$\frac{2p^2 - 3p -b^3}{pb}$

$\frac{2p^3 - 3p^2 -b^3}{p}$

Correct answer:

$\frac{2p^3 - 3p^2 -b^3}{pb}$

Explanation:

To simplify this problem, multiply each term by the denomenator of the other over itself:

$\frac{2p^2 - 3p}{b}(\frac{p}{p}) - \frac{b^2}{p}(\frac{b}{b})$

Then you will yield terms with a like denomenator, which can be combined:

$\frac{2p^3 - 3p^2}{pb} - \frac{b^3}{pb}$

$\frac{2p^3 - 3p^2 - b^3}{pb}$

Report an Error

Example Question #13 : Rational Expressions

Choose the answer which best simplifies the expression below:

$\frac{xy^2}{m} - \frac{m^2n}{y}$

Possible Answers:

$\frac{xy^2 - m^2n}{my}$

$\frac{xy^3 - m^3n}{y}$

$\frac{x(y^3 - m^3n)}{my}$

$\frac{xy^3 - m^3n}{my}$

$\frac{xy^3 - m^3n}{m}$

Correct answer:

$\frac{xy^3 - m^3n}{my}$

Explanation:

To simplify the expression, first multiply each term by the denomenator of the other over itself:

$\frac{xy^2}{m}(\frac{y}{y}) - \frac{m^2n}{y}(\frac{m}{m})$

Then you yield terms with common denomenators, which can be combined:

$\frac{xy^3}{my}-\frac{m^3n}{my}$

$\frac{xy^3 - m^3n}{my}$

Report an Error

Example Question #14 : Rational Expressions

Choose the answer which best simplifies the following expression:

$\frac{x^2 + x + 3}{4a}-\frac{2y^2}{7}$

Possible Answers:

$\frac{7x^2 +7x +21-8ya}{28a}$

$\frac{7x^2 +7x +21-8y^2a}{28a}$

$\frac{7x^2 +7x +21-8y^2a}{7a}$

$\frac{x^2 +x +3-8y^2a}{28a}$

$\frac{7x^2 +7x +21-8y^2}{28a}$

Correct answer:

$\frac{7x^2 +7x +21-8y^2a}{28a}$

Explanation:

To simplify, first multiply each of the terms by the denomenator of the other over itself:

$\frac{x^2 + x + 3}{4a}(\frac{7}{7})-\frac{2y^2}{7}(\frac{4a}{4a})$

Then you will get terms with a common denomenator, which can be combined:

$\frac{7x^2 + 7x + 21}{28a}-\frac{8y^2a}{28a}$

$\frac{7x^2 +7x +21-8y^2a}{28a}$

Report an Error

Example Question #11 : Rational Expressions

Choose the answer which best simplifies the expression below:

$\frac{2n^2 - n}{3a^2}-\frac{-n^2}{b}$

Possible Answers:

$\frac{-2n^2b-nb-3a^2n^2}{3a^2b}$

$\frac{2n^2b-nb+3a^2n^2}{3a^2b}$

$\frac{2n^2b+nb+3a^2n^2}{3a^2b}$

$\frac{2n^2b-nb-3a^2n^2}{3a^2b}$

$\frac{2n^2b-nb+3a^2n^2}{3ab}$

Correct answer:

$\frac{2n^2b-nb+3a^2n^2}{3a^2b}$

Explanation:

To simplify, first multiply each of the terms by the denomenator of the other over itself:

$\frac{2n^2 - n}{3a^2}(\frac{b}{b})-\frac{-n^2}{b}(\frac{3a^2}{3a^2})$

You will yield terms with a common denomenator, which can be combined:

$\frac{2n^2b - nb}{3a^2b}-\frac{-3a^2n^2}{3a^2b}$

$\frac{2n^2b-nb+3a^2n^2}{3a^2b}$

Report an Error

Example Question #291 : Algebra

Choose the answer which best simplifies the expression below:

$\frac{2a}{14-y} - \frac{3}{8 +a}$

Possible Answers:

$\frac{2a^2 +16a +3y -42}{-112 - 8y+14a -ay}$

$\frac{2a^2 +16a +3y +42}{112 - 8y+14a -ay}$

$\frac{2a^2 +16a +3y -42}{112 - 8y-14a -ay}$

$\frac{2a^2 +16a -3y -42}{112 - 8y+14a -ay}$

$\frac{2a^2 +16a +3y -42}{112 - 8y+14a -ay}$

Correct answer:

$\frac{2a^2 +16a +3y -42}{112 - 8y+14a -ay}$

Explanation:

To simplify, multiply each of the terms by the denomenator of the other, over itself:

$\frac{2a}{14-y}(\frac{8 +a}{8+a}) - \frac{3}{8 +a}(\frac{14-y}{14-y})$

You will yield terms with a common denomenator, which can be combined:

$\frac{16a +2a^2}{112-8y+14a-ay}-\frac{42-3y}{112-8y+14a-ay}$

$\frac{2a^2 +16a +3y -42}{112 - 8y+14a -ay}$

Report an Error

Example Question #1 : How To Evaluate Rational Expressions

If √(ab) = 8, and a²= b, what is a?

Possible Answers:

Correct answer:

Explanation:

If we plug in a² for b in the radical expression, we get √(a³) = 8. This can be rewritten as a^3/2 = 8. Thus, log_a8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.

Report an Error

Example Question #2 : How To Evaluate Rational Expressions

Function_part1

Possible Answers:

9/5

–37/15

37/15

–9/5

–11/5

Correct answer:

–11/5

Explanation:

Fraction_part2

Fraction_part3

Report an Error

Example Question #1 : Rational Expressions

2x-12=24

3y-15=60

Find the product of and .

Possible Answers:

450

144

120

260

325

Correct answer:

450

Explanation:

Solve the first equation for .

2x-12=24

2x=36

x=18

Solve the second equation for .

3y-15=60

3y=75

y=25

The final step is to multiply and .

xy = (18)(25)=450

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Denver, Reading Tutors in Atlanta, Algebra Tutors in New York City, MCAT Tutors in San Francisco-Bay Area, GRE Tutors in Dallas Fort Worth, Chemistry Tutors in Phoenix, ISEE Tutors in Houston, Calculus Tutors in Philadelphia, SSAT Tutors in Dallas Fort Worth, Math Tutors in Atlanta

Popular Courses & Classes

LSAT Courses & Classes in Philadelphia, GRE Courses & Classes in Los Angeles, GMAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Boston, GRE Courses & Classes in Atlanta, GMAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Phoenix, ISEE Courses & Classes in Dallas Fort Worth

Popular Test Prep

ACT Test Prep in Philadelphia, SAT Test Prep in Seattle, GRE Test Prep in Atlanta, SAT Test Prep in Miami, ACT Test Prep in Seattle, ACT Test Prep in Houston, SSAT Test Prep in Miami, GMAT Test Prep in Miami, LSAT Test Prep in Philadelphia, SSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : Rational Expressions

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #2 : How To Subtract Rational Expressions With Different Denominators

Example Question #2 : How To Subtract Rational Expressions With Different Denominators

Example Question #12 : Rational Expressions

Example Question #13 : Rational Expressions

Example Question #14 : Rational Expressions

Example Question #11 : Rational Expressions

Example Question #291 : Algebra

Example Question #1 : How To Evaluate Rational Expressions

Example Question #2 : How To Evaluate Rational Expressions

Example Question #1 : Rational Expressions

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details