All GRE Math Resources
Example Questions
Example Question #11 : How To Find Decimal Fractions
Convert 
First convert this decimal number to a mixed number fraction, then covert the mixed number to an improper fraction. The mixed number fraction must have a whole number of 

Example Question #991 : Gre Quantitative Reasoning
Convert the mixed fraction 
Since the starting number is a mixed number fraction, the decimal number must also have a value in the ones place. Since the denominator in the fraction has a value that is a factor of 


Example Question #11 : Decimals With Fractions
A retailer can only order wristbands in bulk cases. Each case has 300 wristbands and costs $1172.
Quantity A: The number of wristbands that can be bought for $10547.
Quantity B: The number of wristbands that can be bought for $10560.
The two quantities are equal.
Quantity B is greater.
Quantity A is greater.
The relationship cannot be determined.
Quantity B is greater.
The key to this problem is to realize that the store cannot buy partial crates of wristbands--it's all or nothing. Calculate how many crates can be bought with each sum of money by dividing the sum by the price of a crate.
Quantity A:
Although oh so close, only eight crates can be bought with this sum of money. Don't round up!
Quantity B:
There's just enough to buy nine crates.
Quantity B is greater.
Example Question #1 : How To Find The Fractional Equivalent Of A Decimal
A tub of food contains 


To begin with, it is easiest just to add these decimals together using your calculator:
Now, this is the same thing as:
We can rewrite this:
To find this, you need to give the two numbers a common denominator:
This is your answer.
Example Question #1 : How To Find The Fractional Equivalent Of A Decimal
What is the fractional equivalent of 
In decimal form 
This is equal to

This fraction cannot be reduced any further therefore it is in its final answer form.
Example Question #2 : How To Find The Fractional Equivalent Of A Decimal
Choose the answer which best converts the following decimal into a fraction, ensure that you simplify your answer:
To convert a decimal into a fraction, simply put the digits of the decimal in the numerator of a fraction, then one followed by a number of zeroes equal to the number of digits in the decimal as your denomator. In this case:
Then, you can simplify, as both 


Example Question #411 : Arithmetic
Simplify the following expression:
It can help to begin by writing the expression using scientific notation:
Now remove common divisors from the numerator and denominator:
Example Question #1 : Decimals With Fractions
If 
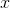
None of the other answer choices are correct
Convert all of the fractions to decimals. Thus, x is contained within the range of 0.33 < x < 0.76. The answers choices become 1/4 = 0.25, 4/12 = 0.33, 2/5 = 0.4, and 5/16 = 0.3125, respectively. Therefore, the only answer which is within the desired range is 2/5.
Example Question #12 : Decimals With Fractions
Vega only purchases gardening claws in bulk cases. Each case is 150 claws for $2415.17.
Quantity A: The number of claws Vega can purchase with $41,082.05
Quantity B: The number of claws Vega can purchase with $43,473.05
The relationship cannot be determined.
Quantity B is greater.
Quantity A is greater.
The two quantities are equal.
The two quantities are equal.
Looking at the differences in prices, one might guess that Quantity B is the answer. Beware the easy answer; always check.
Instead, calculating how many cases of claws Vega can buy, keeping in mind that he cannot purchase part of a case. Do not round up!
Quantity A:
Quantity B:
In either case, he can buy no more than seventeen cases. The two quantities are equal.
Example Question #13 : Decimals With Fractions
Isley only buys seeds for her gardening store in bulk cases, with each case containing 
Quantity A: The number of seeds Isley can purchase with $3837.54
Quantity B: The number of seeds Isley can purchase with $3871.86
The two quantities are equal.
Quantity B is greater.
Quantity A is greater.
The relationship cannot be determined.
The two quantities are equal.
Looking at how close the dollar values are for A and B, it's tempting to think the GRE is being tricky, and that B will allow for the purchase of more cases of seeds.
Do not assume; check to see whether or not this is the situation. Note that a portion of a case cannot be purchased; round down to the nearest integer when calculating how many cases may be bought.
Since each case is $343.25
Quantity A:
Quantity B:
The two quantities are equal.
All GRE Math Resources


























































