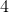GRE Math : Integers
Study concepts, example questions & explanations for GRE Math
All GRE Math Resources
Example Questions
Example Question #1 : How To Divide Even Numbers
Choose the answer below which best solves the following equation:
To solve this problem, set up long division for yourself. First, you know that your hundreds digit of the solution will be one, as twelve goes into seventeen one time. Then, you take twelve away from seventeen, and are left with three remaining. Bring down your next digit over from the dividend, and you are left with thirty two, which twelve goes into four times. Already, you know that the answer has to be 
Example Question #2 : How To Divide Even Numbers
Solve for 
To solve, first isolate the variable by dividing both sides of the equation by 
As a check, know that any time you divide an even number by another even number, you will get an even result.
Example Question #3 : How To Divide Even Numbers
Solve for 
To solve, isolate your variable by dividing both sides of the equation by 
As a check, know that any time you divide an even number by another even number, the result will be even.
Example Question #4 : How To Divide Even Numbers
Solve for 
To solve, isolate the variable by dividing both sides of the equation by 
As a check, know that any time you divide an even number by another even number, the result will be even.
Example Question #1 : How To Divide Even Numbers
Solve for 
To solve, isolate the variable by dividing both sides of your equation by 
As a check, know that any time you divide an even number by another even number, your result will be even.
Example Question #6 : How To Divide Even Numbers
Assume 
What is a possible solution of 
Since 
Example Question #1 : How To Find The Missing Number In A Set
The product of two integers is 14. Which of the following could be the average of the two numbers?
The two integers in this case, and their respective averages, could be:
Only 
Example Question #1 : How To Find The Missing Number In A Set
Which of these is a natural number?
All of these are natural numbers.
None of these are natural numbers .
The natural numbers are the positive integers (whole numbers) starting with 1.
Example Question #3 : How To Find The Missing Number In A Set
Which of the following pairs of events are mutually exclusive?
the positive numbers, the numbers less than
the negative numbers,
the even numbers, the numbers greater than
the numbers less than 
the positive numbers, the numbers less than
We can think of mutually exclusive in terms of a Venn diagram. We are looking for the pair of events that has nothing in common. The only sets that don't have a single number in common are the positive numbers and the numbers less than –200.
Example Question #1 : Sets
In the set of positive, distinct integers 
We know that all the numbers are positive, so they are greater than zero. We also know that the numbers are distinct, so they are all unique.
We can write this as {a + b + 8 + d + e}, so let a and b be 1 and 2 respectively, the smallest possible positive, distinct integers. Then let d and e be 9 and 10, the smallest positive, distinct integers larger than 8.
We add the set {1 + 2 + 8 + 9 + 10} to find it equals 30.
All GRE Math Resources
