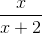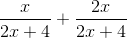All GRE Math Resources
Example Questions
Example Question #31 : Rational Expressions
Evaluate 

To solve, simply plug in 

First we must simplify the exponents. The we will multiply each of the two terms in the numerator. After that, we can add the terms in denominator and subtract the terms in the numerator.
Sutracting the terms on top gives:

We can simplify this fraction by factoring out a sixteen from both the numerator and denominator.
Example Question #31 : Expressions
Simplify the expression.
To add rational expressions, first find the least common denominator. Because the denominator of the first fraction factors to 2(x+2), it is clear that this is the common denominator. Therefore, multiply the numerator and denominator of the second fraction by 2.
This is the most simplified version of the rational expression.
Example Question #1 : Expressions
Simplify the following:
To simplify the following, a common denominator must be achieved. In this case, the first term must be multiplied by (x+2) in both the numerator and denominator and likewise with the second term with (x-3).
Example Question #311 : Gre Quantitative Reasoning
Choose the answer which best simplifies the following expression:
To simplify, first multiply both terms by the denominator of the other term over itself:
Then, you can combine the terms, now that they share a denominator:
Example Question #312 : Gre Quantitative Reasoning
Choose the answer which best simplifies the following expression:
To simplify this expression, you have to get both numerators over a common denominator. The best way to go about doing so is to multiply both expressions by the others denominator over itself:
Then you are left with:
Which you can simplify into:
From there, you can take out a 
Which gives you your final answer:
Example Question #313 : Gre Quantitative Reasoning
Choose the answer which best simplifies the following expression:
To solve this problem, first multiply both terms of the expression by the denominator of the other over itself:
Now that both terms have a common denominator, you can add them together:
Example Question #33 : Expressions
Simplify (4x)/(x2 – 4) * (x + 2)/(x2 – 2x)
4/(x + 2)2
x/(x – 2)2
(4x2 + 8x)/(x4 + 8x)
x/(x + 2)
4/(x – 2)2
4/(x – 2)2
Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.
Example Question #3 : Expressions
what is 6/8 X 20/3
6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)
3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)
1/1 X 5/1 = 5
Example Question #31 : Expressions
Multiply
When multiplying two binomials, it's best to remember the mnemonic FOIL, which stands for First, Outer, Inner, and Last. Going in the order of FOIL, we multiply the first term of each binomial, then the outer terms of the expression, then the inner terms of the expression, and finally the last term of each binomial. For this question we get: 
Example Question #2 : How To Multiply Rational Expressions
Express the following as a single rational expression, make sure you simplify your answer:
To do this problem, simply multiply as you would with any fraction, combining like terms whenever possible:
When multiplying, make sure to distribute through to all terms in the polynomial.
Then you can factor out a six to simplify for your final answer:
All GRE Math Resources