GMAT Math : Geometry
Study concepts, example questions & explanations for GMAT Math
All GMAT Math Resources
Example Questions
Example Question #6 : Dsq: Calculating The Area Of A Square
True or false:
Statement 1: A square with sidelength 
Statement 2: A square with sidelength 
EITHER STATEMENT ALONE provides sufficient information to answer the question.
BOTH STATEMENTS TOGETHER provide sufficient information to answer the question, but NEITHER STATEMENT ALONE provides sufficient information to answer the question.
STATEMENT 2 ALONE provides sufficient information to answer the question, but STATEMENT 1 ALONE does NOT provide sufficient information to answer the question.
STATEMENT 1 ALONE provides sufficient information to answer the question, but STATEMENT 2 ALONE does NOT provide sufficient information to answer the question.
BOTH STATEMENTS TOGETHER do NOT provide sufficient information to answer the question.
STATEMENT 1 ALONE provides sufficient information to answer the question, but STATEMENT 2 ALONE does NOT provide sufficient information to answer the question.
Assume Statement 1 alone. The perimeter of a square is four times the length of a side, which here is 
Therefore, the question can be answered in the affirmative from Statement 1 alone.
Statement 2 alone gives insufficient information, however. The area of a square is the square of the length of a side. If the sidelength is 
Example Question #12 : Quadrilaterals
Gene is building a fence. He is using square fence posts and needs to know the total distance around one pole. Help him find the distance,
I) The fence will be 
II) The diagonal distance from one corner of a fence post to its other corner is 
Either statement is sufficient to answer the question.
Both statements are needed to answer the question.
Neither statement is sufficient to answer the question. More information is needed.
Statement II is sufficient to answer the question, but statement I is not sufficient to answer the question.
Statement I is sufficient to answer the question, but statement II is not sufficient to answer the question.
Statement II is sufficient to answer the question, but statement I is not sufficient to answer the question.
We are asked to find the perimeter of a square. To do that we need a side length.
I) Is irrelevant and is trying to distract you with other aspects of the question.
II) Gives you the diagonal of the square. The diagonal of a square creates two 45/45/90 triangles.
Use this knowledge to find the other side lengths and then the perimeter.
Example Question #13 : Quadrilaterals
Find the perimeter of the square.
- The length of the diagonal of the square is
.
- The area of the square is
.
Each statement alone is sufficient to answer the question.
Statements 1 and 2 are not sufficient, and additional data is needed to answer the question.
Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
Statement 2 alone is sufficient, but statement 1 alone is not sufficient to answer the question.
Both statements taken together are sufficient to answer the question, but neither statement alone is sufficient.
Each statement alone is sufficient to answer the question.
Statement 1: The length of the diagonal of a square is found by multiplying the length of one side by the square root of 
Knowing the length of the side, we can find the perimeter of the square:
Statement 2: We can use the given area to solve for the length of the side
where 
We can now find the perimeter in the same manner:
Therefore, each statement alone is sufficient to answer the question.
Example Question #2291 : Gmat Quantitative Reasoning
The ratio of square A to square B is 3:1. Find the perimeter of square B.
- The area of square A is
.
- The length of the diagonal of square B is
.
Each statement alone is sufficient to answer the question.
Both statements taken together are sufficient to answer the question, but neither statement alone is sufficient.
Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
Statements 1 and 2 are not sufficient, and additional data is needed to answer the question.
Statement 2 alone is sufficient, but statement 1 alone is not sufficient to answer the question.
Each statement alone is sufficient to answer the question.
Statement 1: We can use the area to find the length of square A's side.
Keep in mind that the ratio of square A to square B is 3:1.
Now that we know the length of the side, we can find the perimeter of square B.
Statement 2: We can use the diagonal to find the length of the side.
We can easily see the side measures 
Example Question #2292 : Gmat Quantitative Reasoning
What is the perimeter of the square?
- A side measures
.
- The area of the square is
.
Each statement alone is sufficient to answer the question.
Statements 1 and 2 are not sufficient, and additional data is needed to answer the question.
Statement 2 alone is sufficient, but statement 1 alone is not sufficient to answer the question.
Both statements taken together are sufficient to answer the question, but neither statement alone is sufficient.
Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
Each statement alone is sufficient to answer the question.
Recall the formula for perimeter of a square:
where 
Statement 1: We're given 
Statement 2: We're given the area 
With 
Each statement alone is sufficient to answer the question.
Example Question #5 : Dsq: Calculating The Perimeter Of A Square
Find the perimeter of the square.
- The diagonal measures
inches.
- The diagonal is found by
where
represents a square's side length.
Both statements taken together are sufficient to answer the question, but neither statement alone is sufficient.
Each statement alone is sufficient to answer the question.
Statements 1 and 2 are not sufficient, and additional data is needed to answer the question.
Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
Statement 2 alone is sufficient, but statement 1 alone is not sufficient to answer the question.
Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
Statement 1: We can find the length of the square's side using the information given.
so
We can now find the perimeter of the square: 
Statement 2: In order to find the length of the square's side using the information provided in Statement 1, we need to use this equation.
Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
Example Question #61 : Geometry
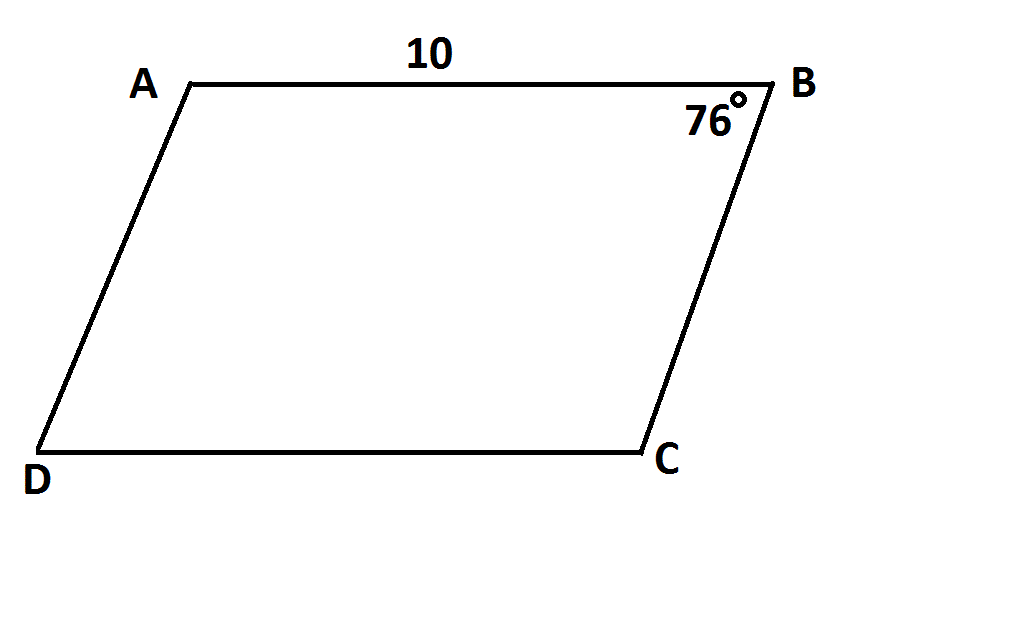
NOTE: Figure NOT drawn to scale.
Is the above figure a parallelogram?
Statement 1:
Statement 2:
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Knowing one pair of sides of a quadrilateral to be congruent is not alone sufficient to prove that figure to be a parallelogram, nor is knowing one pair of sides of a quadrilateral to be parallel. But knowing both about the same pair of sides is sufficient by a theorem of parallelograms.
Example Question #62 : Geometry
Notes: 
Calculate 
Statement 1:
Statement 2: The area of the trapezoid is 7,000.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Consider the area formula for a trapezoid:
So, if you know both the area and 
Example Question #1 : Dsq: Calculating The Length Of The Side Of A Quadrilateral
Consider parallelogram 
I) The perimeter of 
II) Side 
Find the length of side 
Statement II is sufficient to answer the question, but statement I is not sufficient to answer the question.
Statement I is sufficient to answer the question, but statement II is not sufficient to answer the question.
Either statement is sufficient to answer the question.
Neither statement is sufficient to answer the question. More information is needed.
Both statements are needed to answer the question.
Both statements are needed to answer the question.
We can work backwards from the perimeter to find the length of the unknown side.
I) Gives us the perimeter.
II) Gives us two of the sides.
In a parallelogram there are two sets of corresponding sides. We can use I) and II) to write the following equaiton, where l is the length of our wanted side.
Solve for l to find our final side:
Example Question #1 : Dsq: Calculating The Length Of The Side Of A Quadrilateral
Calculate the side of a square.
Statement 1: A circle with an area of 
Statement 2: A circle with a circumference of 
Statement 1: A circle with an area of 
Write the formula for the area of the circle.
After substituting the value of the area and solve for radius, the radius is 1. The side length of the square is double the length of the radius.
Statement 2: A circle with a circumference of 
Write the formula for the circumference of the circle.
After substituting the value of the circumference and solve for diameter, the diameter of the circle is 1. This diameter represents the diagonal of the square. Because the square length and width are equal dimensions, it is possible to solve for the lengths of the square by Pythagorean Theorem knowing just the length of the square diagonal.
Therefore:
All GMAT Math Resources
