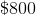GRE Math : Percent of Change

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 Next →

Example Question #71 : Percentage

A city originally had a $6\%$ sales tax, but increased it to $8\%$ . Assuming that the rate of consumption in the city does not change, what was the total amount of sales tax collected when the rate was $6\%$ if the increase in tax brought in an additional $\$150,000$ in revenue?

Possible Answers:

$\$550,000$

$\$500,000$

$\$7,500,000$

$\$1,200,000$

$\$450,000$

Correct answer:

$\$450,000$

Explanation:

One way to solve this is by considering that the increase in taxes is a linear addition of 2%. Therefore we can ask the question, 2% of what amount yields $150,000? This can be represented in the following equation:

0.02 * x = 150,000

Solve for x: $7,500,000

Therefore, the total at the old rate is 7,500,000 * 0.06 = $450,000.

Report an Error

Example Question #71 : Percentage

In 2014, approximately $27.7\%$ of Americans were considered charming. In 2013 approximately 27.1% of Americans were deemed charming. If the population of America in 2013 was $\textup{316.5 million}$ people and the population of America in 2014 was roughly $\textup{318.9 million}$ people, what is the percent increase/decrease of charming people from 2013-2014? Round to the nearest tenth.

Possible Answers:

$0.6\%$

$2.9\%$

$\textup{Cannot be determined with the information provided}$

$3.1\%$

$3.0\%$

Correct answer:

$3.0\%$

Explanation:

To solve this problem, we must understand that we can't simply use the percentage change from 2013-2014 in order to solve this problem. Because the populations change, simply using the percentage change in order to is invalid. Therefore we must find the amount of people that were charming in each year to solve for this problem.

In 2013, $27.1\%$ of the $\textup{316.5 million}$ people in America were considered charming, this means that the number of charming people in America in 2013 is 0.271*316.5=85.7715 $\textup{million}$ people.

In 2014, $27.7\%$ of the $\textup{318.9 million}$ people in America were considered charming, this means that the number of charming people in America in 2014 is 0.277*318.9=88.3353 $\textup{million}$ people.

Therefore to find the percent increase of charming people, we simply find the difference in charming people from 2013-2014 and divide by the number of charming people in 2013. $\frac{88.3353-85.7715}{85.7715}=\frac{2.5638}{85.7715}=0.02989$ or a $2.989\%$ increase in charming people.

Report an Error

Example Question #73 : Percentage

A new TV at some store goes on sale for $10\%$ off the retail price. A customer comes in to buy the TV, and in addition to the store discount of $10\%$ , uses a coupon for an extra $\$200$ off. The customer ends up paying $65\%$ of the original price of the TV. What is the original price of the TV?

Possible Answers:

$\$1050$

$\$700$

$\$1000$

$\$800$

$\$750$

Correct answer:

$\$800$

Explanation:

Let represent the original price of the TV. Now, set up an equation where the discounted price of the TV (10% discount) minus 200 dollars is equal to 65% of the original price of the TV:

0.9x-200=.65x

Solve for

0.9x-200+200=0.65x+200

0.9x=0.65x+200

0.9x-0.65x=200

0.25x=200

x=800

The original price of the TV is $\$800$ .

Report an Error

← Previous 1 2 Next →

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Los Angeles, Algebra Tutors in Denver, MCAT Tutors in New York City, Spanish Tutors in Chicago, English Tutors in Miami, Biology Tutors in Los Angeles, ISEE Tutors in Dallas Fort Worth, English Tutors in New York City, Statistics Tutors in Philadelphia, Spanish Tutors in Atlanta

Popular Courses & Classes

LSAT Courses & Classes in Boston, MCAT Courses & Classes in Atlanta, ACT Courses & Classes in Houston, GRE Courses & Classes in Los Angeles, GMAT Courses & Classes in Houston, SAT Courses & Classes in Houston, SAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in San Diego, GMAT Courses & Classes in San Diego

Popular Test Prep

MCAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Philadelphia, LSAT Test Prep in Seattle, MCAT Test Prep in Washington DC, GRE Test Prep in Los Angeles, ACT Test Prep in Houston, GMAT Test Prep in San Diego, GMAT Test Prep in Denver, GMAT Test Prep in Miami, ISEE Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : Percent of Change

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #71 : Percentage

Example Question #71 : Percentage

Example Question #73 : Percentage

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details