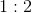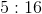All GRE Math Resources
Example Questions
Example Question #111 : Fractions
There are 3,500 people in group A and 5,000 people in group B:
|
Car Type |
% in Group A Who Own |
% in Group B Who Own |
|
Motorbike |
4 |
9 |
|
Sedan |
35 |
25 |
|
Minivan |
22 |
15 |
|
Van |
9 |
12 |
|
Coupe |
3 |
6 |
What is the ratio of the number of people in group A with motorbikes and vans to the total number of people across both groups with motorbikes and vans?
First find the total number that own both motorbikes and vans of each group separately:
Group A:
Group B:
Now we have a ratio that should be:
Example Question #1 : How To Find A Ratio
A dessert is made using 2 parts cake and 3 parts icing. The cake contains 4 parts sugar, 5 parts milk, and 11 parts of other ingredients. The icing contains 3 parts sugar, 2 parts milk, and 15 parts of other ingredients. Which quantity is greater?
Quantity A: Parts sugar in the dessert
Quantity B: Parts milk in the dessert
The relationship cannot be determined from the information given.
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
Quantity A is greater.
Quantity A: To determine the parts of sugar in the dessert, we use the following process. Let's first figure out the amount of sugar in the cake. This is 4/20. Next, find the amount of sugar in the icing topping: 3/20. Then, we need to account for the amount of cake and icing in the dessert. Using the fact that there are 2 parts cake and 3 parts icing, we can say that 2/5 of the dessert is cake and 3/5 is icing. Combining this information with the amount of sugar in both the cake and the icing, we obtain: 2/5 * 4/20 + 3/5 * 3/20 = 17/100. So, there are 17 parts of sugar in the dessert.
Quantity B: Use the same method to find the amount of milk: 2/5 * 5/20 + 3/5 * 2/20 = 16/100. So there are 16 parts milk in the dessert. Thus, Quantity A is larger.
Example Question #112 : Fractions
The ratio of the number of financial employees who remained in the same role for 2 to 9 years to the number of construction employees who remained in the same role for 0 to 4 years is closest to which of the following?
For this problem, we need to find the number of employees who fall into the categories described, keeping in mind that multiple portions of the pie chart must be accommodated for. Then, we can fit them into a ratio:
For the "2 to 9 years" portion of the financial industry, include
(0.2 + 0.18)(12,000,000) = 4,560,000 workers.
For the "0 to 4 years" portion of the construction industry, include
(0.15 + 0.2)(8,000,000) = 2,800,000 workers.
Now divide and simplify to find the ratio:
4,560,000/2,800,000 = 8/5.
Example Question #12 : Proportion / Ratio / Rate
The ratio of 







What is the ratio of 

Since the ratios are fixed, regardless of the actual values of 



In order to convert to a form where we can relate 







Thus, we now have 

Setting the 

Example Question #1111 : Gre Quantitative Reasoning
A fence has a post that is 5 in wide. The fence is constructed with 5 foot pieces. What is a possible length of a straight fence if it starts and ends with a post with a post between each piece of fence.
You must convert all the measurements to inches first so the fence pieces will be 

For one piece of fence, it would be two posts and one fence piece

For two pieces of fence, it would be three posts and two pieces of fence which would be the answer of

Example Question #21 : Proportion / Ratio / Rate
Two cars begin 500 miles apart and begin driving directly toward each other. One car proceeds at a rate of 50 miles per hour, while the other proceeds at a rate of 40 miles per hour. Rounding down, many minutes will it take for the two drivers to be 150 miles apart?
333
250
300
233
233
You know that the distance between these cars is defined by the following equation: Answer "250" = 500 – 90t. This is because the cars get 90 miles closer every t hours. You want to solve for t when the distance is 150: 150 = 500 – 90t; –350 = –90t; t = 35/9. Recall, however, that the question asked for the rounded-down number of minutes; therefore, multiply your answer by 60: 35 * 60/9 = 2331/3
Rounding down, you get 233.
Example Question #22 : Proportion / Ratio / Rate
If Mary has $17 and gains a $2 weekly allowance, while Todd has $4 and gains a $3 weekly allowance, what is the least number of weeks that will pass before Todd has more money than Mary?
16
15
12
14
13
14
First we set up two equations, one for Mary and one for Todd. Mary’s money growth is represented by y = 2x + 17 (she starts with $17 so this is our y-intercept and she gains $2 weekly so this is our slope).
Todd’s money growth is represented by y = 3x + 4 (he starts with $4 so this is our y-intercept and he gains $3 weekly so this is our slope). Set these two equal and solve for x. We find that after 13 weeks they have the same amount of money. But this is not what the question asked for. They want to know how many weeks it will take before Todd has MORE than Mary. Thus the answer must be 14 weeks.
Example Question #112 : Fractions
At a widget factory, 60 workers produce 1,000 widgets per week using power from internal generators. If (f) cubic meters of fuel are required by (g) number of generators every day to power the factory, how long will (t) cubic meters of fuel last in days?
t/fg
g/tf
tg/f
f/tg
tf/g
t/fg
This is a plug and chug sort of problem, where choosing values is arbitrary. Suppose the generators consume 5 cubic meters of fuel per day and there are 10 generators. Then the number of days that 100 cubic meters of fuel will last is expressed as 100/5*10. Switching back to variables, that comes out to t/fg.
Example Question #31 : Proportion / Ratio / Rate
Beverly just filled up her gas tank, which has enough gas to last her, at her usual driving rate, about 45 days. However, Beverly becomes extra busy and begins driving 66.6% more than she usually does. How many days does the tank of gas last Beverly at her new rate?
10 days
30 days
33 days
15 days
27 days
27 days
Answer: 27 days
Explanation: Recall that the rate of gas consumption is INVERSELY related to the time it takes to consume the gas. Thus, if the rate of gas consumption increases to 5/3 of it's original rate (a 66.6% increase), then the time it will take to consume all of the gas decreases to the inverse, or 3/5 of the original. The answer is thus 27 (3/5 of 45).
Example Question #31 : Proportion / Ratio / Rate
A Super Sweet Candy Puff Roll has 1450 calories per roll. A man eats one roll in 10 minutes. During the work day, the man eats a roll at the start of the shift and then eats another a roll every two hours after finishing the last one. Since he is watching his health, he eats only until 3 PM but will not start eating another one at any time after 3 PM. If his shift begins at 8 AM and ends at 5 PM, how many calories per minute does he consume in Super Sweet Candy Puff Rolls® during the whole work day?
14.27
5800
13.43
10.74
9.21
10.74
It is probably easiest just to write out the eating schedule:
Roll 1: 8:00 AM - 8:10 AM
Roll 2: 10:10 AM - 10:20 AM
Roll 3: 12:20 PM - 12:30 PM
Roll 4: 2:40 PM - 2:50 PM
Therefore, he eats 4 rolls, or 1450 * 4 = 5800 calories. To get the rate, this must be divided across the whole day's minutes: 9 work hours * 60 = 540 minutes. The average calories per minute = 10.74.
All GRE Math Resources