All GRE Math Resources
Example Questions
Example Question #1 : Pentagons
In a five-sided polygon, one angle measures 
To find the sum of the interior angles of any polygon, use the formula 
In this case:
The sum of the interior angles will be 540. Go through each answer choice and see which one adds up to 540 (including the original angle given in the problem).
The only one that does is 120, 115, 95, 105 and the original angle of 105.
Example Question #52 : Plane Geometry
In a particular heptagon (a seven-sided polygon) the sum of four equal interior angles, each equal to 
Quantity A:
Quantity B:
The two quantities are equal.
Quantity A is greater.
The relationship cannot be determined.
Quantity B is greater
Quantity A is greater.
The sum of interior angles in a heptagon is 


Three interior angles (call them 

Further more, all of these angles must sum up to 
We may not be able to find 



Example Question #53 : Geometry

What is the value of 
Always begin working through problems like this by filling in all available information. We know that we can fill in two of the angles, giving us the following figure:

Now, we know that for any polygon, the total number of degrees in the figure can be calculated by the equation:


Thus, for our figure, we have:
Based on this, we know:
Simplifying, we get:
Solving for 

Example Question #53 : Plane Geometry

Quantity A: The measure of the largest angle in the figure above.
Quantity B:
Which of the following is true?
Quantity B is larger.
The relationship cannot be determined.
Quantity A is larger.
The two quantities are equal.
Quantity A is larger.

To begin, recall that the total degrees in any figure can be calculated by:


Now, based on our figure, we can make the equation:
Simplifying, we get:

This means that 

Example Question #1 : Triangles
What is the perimeter of an isosceles triangle given that the sides 5 units long and half of the base measures to 4 units?
The base of the triangle is 4 + 4 = 8 so the total perimeter is 5 + 5 + 8 = 18.
Example Question #1 : Isosceles Triangles
An acute Isosceles triangle has two sides with length 
. The length of side










This Isosceles triangle has two sides with a length of 
To find the missing side, double the value of side 


Therefore, this triangle has two sides with lengths of 

To find the perimeter, apply the formula: 

Example Question #57 : Geometry
An acute Isosceles triangle has two sides with length 
. The length of side




To solve this problem apply the formula: 
However, first calculate the length of the missing side by: 
Thus, the solution is:
Example Question #58 : Geometry
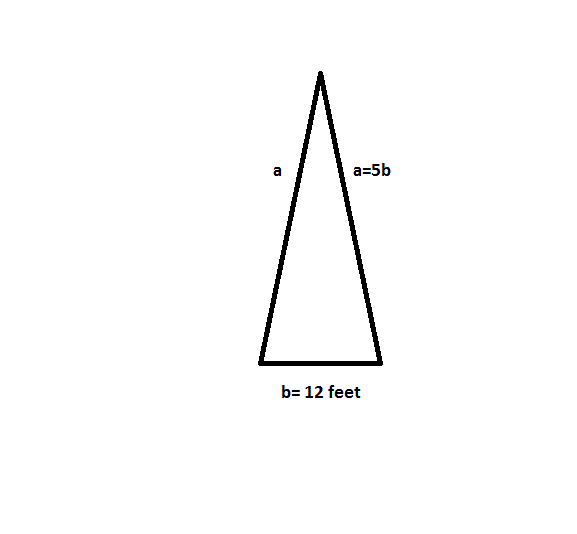
Find the perimeter of the acute Isosceles triangle shown above.
To solve this problem apply the formula: 
However, first calculate the length of the missing side by:
Example Question #2 : Isosceles Triangles
An obtuse Isosceles triangle has two sides with length 
. The length of side









By definition, an Isosceles triangle must have two equivalent side lengths. Since we are told that 







Now, apply the formula: 
Then, simplify the fraction/convert to mixed number fraction:
Example Question #60 : Geometry
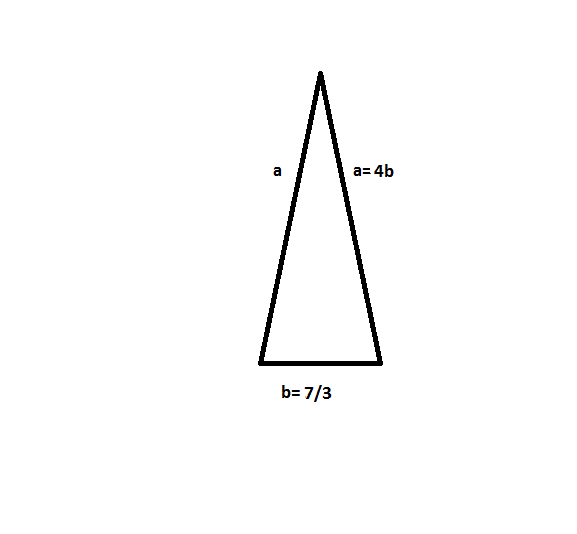
Find the perimeter of the acute Isosceles triangle shown above.
In order to solve this problem, first find the length of the missing sides. Then apply the formula:
Each of the missing sides equal: 
Then apply the perimeter formula:
All GRE Math Resources






















































