The radius  of a circle with area  can be found as follows:

The circle, the central angle, and the chord are shown below:

By way of the Isosceles Triangle Theorem,  can be proved equilateral, so , the correct response.

The radius  of a circle with area  can be found as follows:

The circle, the central angle, and the chord are shown below, along with , which bisects isosceles 

We concentrate on , a 30-60-90 triangle. By the 30-60-90 Theorem,

and 

The chord  has length twice this, or

A circle with circumference  has as its radius

.

The circle, the central angle, and the chord are shown below, along with , which bisects isosceles :

We concentrate on , a 30-60-90 triangle. By the 30-60-90 Theorem,

 has half the length of , so 

and 

The chord  has length twice this, or

The radius  of a circle with area  can be found as follows:

The circle, the central angle, and the chord are shown below:

By way of the Isosceles Triangle Theorem,  can be proved a 45-45-90 triangle with legs of length . Its hypotenuse has length  times this, or

This is the correct response.

A circle with circumference  has as its radius

.

The circle, the central angle, and the chord are shown below:

By way of the Isosceles Triangle Theorem,  can be proved a 45-45-90 triangle with legs of length 30. By the 45-45-90 Theorem, its hypotenuse - the chord of the central angle - has length  times this, or . This is the correct response.

This is a triangle question in disguise. We have a ninety-degree triangle with two sides made up of the radii of the circle. This means the other two angles ( and ) must be  each. 

Use the 45/45/90 triangle ratios to find the final side. Additionally, you could use Pythagorean Theorem to find the missing side.

45/45/90 side length ratios: 

Segment 

Or, using the Pythagorean Theorem,  by rearranging it and solving for , the hypotenuse, which in this case is segment :

We are given the radius of the circle and the perpendicular distance from its center to the chord, which is all we need to calculate the length of the chord. Using the formula for chord length that involves these two quantities, we find the solution as follows, where  is the chord length,  is the perpendicular distance from the center of the circle to the chord, and  is the radius:

A circle with circumference  has as its radius

.

The circle, the central angle, and the chord are shown below:

By way of the Isosceles Triangle Theorem,  can be proved equilateral, so , the correct response.

The figure referenced is below.

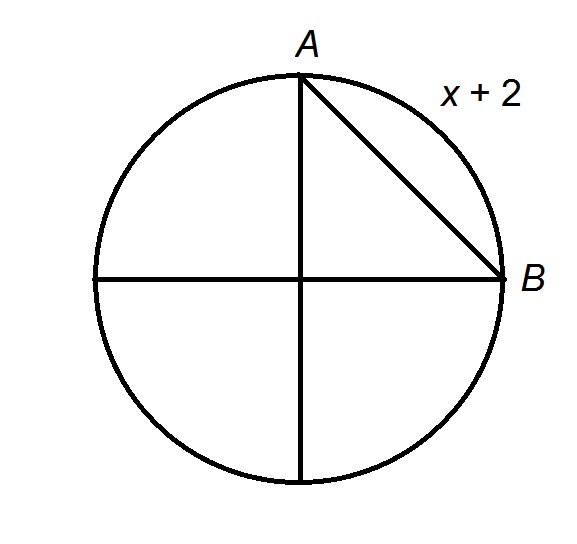
The arc is  of the circle, so the circumference of the circle is

.

The radius is this circumference divided by , or

.

 is, consequently, the hypotenuse of an isosceles right triangle with leg length ; by the 45-45-90 Triangle Theorem, its length is  times this, or

The ratio of the areas of similar rectangles is the square of the similarity ratio, so the ratio of the area of  to that of  is 

.

So if the area of  is , the area of  is 

The area of the shaded region is the difference between the areas of the rectangles, making this area

.

The desired ratio is 24 to 25.