Number Sense - TACHS Math
Card 0 of 32
Examine the decimal
What is the place value of the position occupied by the "6"?
Examine the decimal
What is the place value of the position occupied by the "6"?
Tap to see back →
After the decimal point, the place values of the digits are, in order:
...
The "6" is in the fourth place after the decimal point, so its place value is one ten-thousandth.
After the decimal point, the place values of the digits are, in order:
The "6" is in the fourth place after the decimal point, so its place value is one ten-thousandth.
Solve:
Solve:
Tap to see back →
The lines on either side of the negative integer represent that we need to find its absolute value. The absolute value of a number is its real distance from zero on a number line; therefore, we need to calculate how many spaces the number is tot he left of zero on a number line. This number is a distance from zero and will not be negative. All absolute values are positive.
Therefore, the absolute value—or distance from zero—is the following:
The lines on either side of the negative integer represent that we need to find its absolute value. The absolute value of a number is its real distance from zero on a number line; therefore, we need to calculate how many spaces the number is tot he left of zero on a number line. This number is a distance from zero and will not be negative. All absolute values are positive.
Therefore, the absolute value—or distance from zero—is the following:
Which of the following is equivalent to 
?
Which of the following is equivalent to
Tap to see back →
Recall that when a number is raised to an exponent, that means we will need to multiply the number the number of times that is equal to the exponent.
Thus, with 
, this means we will need to multiply 
by itself four times:
Recall that when a number is raised to an exponent, that means we will need to multiply the number the number of times that is equal to the exponent.
Thus, with
What is the greatest common factor of 
and 
?
What is the greatest common factor of
Tap to see back →
Start by listing out the factors of 
.
Next, list out the factors of 
.
Now, find the largest factor that the two numbers share. In this case, the greatest common factor is 
.
Start by listing out the factors of
Next, list out the factors of
Now, find the largest factor that the two numbers share. In this case, the greatest common factor is
What is the least common multiple of 
and 
?
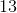What is the least common multiple of
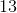
Tap to see back →
Start by listing out multiples of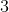 
:
Next, list out multiples of 
:
Now, find the smallest number that is found in both lists. In this case, the least common multiple must be 
.
Start by listing out multiples of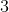
Next, list out multiples of
Now, find the smallest number that is found in both lists. In this case, the least common multiple must be
Give the next number in the sequence:
Give the next number in the sequence:
Tap to see back →
To form the sequence, begin with the term 8. Each subsequent term is equal to 9 added to the previous term, as follows:
,
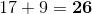
the missing term.
To form the sequence, begin with the term 8. Each subsequent term is equal to 9 added to the previous term, as follows:
the missing term.
Solve for the missing variable in the following proportion:
Solve for the missing variable in the following proportion:
Tap to see back →
Proportions are ratios that are equal to one another. We can solve for the missing variable by using cross multiplication to develop an equation.
Simplify.
Divide both sides of the equation by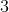 
.
Solve.
Proportions are ratios that are equal to one another. We can solve for the missing variable by using cross multiplication to develop an equation.
Simplify.
Divide both sides of the equation by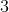
Solve.
Which of the following is equal to six thousand seven ten-thousandths?
Which of the following is equal to six thousand seven ten-thousandths?
Tap to see back →
"Six thousand seven ten-thousandths" in fraction form is 
. To write this in decimal form, put the "7" in the ten-thousandths place, which is the fourth place after the decimal point. This number is "0.6007."
"Six thousand seven ten-thousandths" in fraction form is
Solve:
Solve:
Tap to see back →
The lines on either side of the negative integer represent that we need to find its absolute value. The absolute value of a number is its real distance from zero on a number line; therefore, we need to calculate how many spaces the number is tot he left of zero on a number line. This number is a distance from zero and will not be negative. All absolute values are positive.
Therefore, the absolute value—or distance from zero—is the following:
The lines on either side of the negative integer represent that we need to find its absolute value. The absolute value of a number is its real distance from zero on a number line; therefore, we need to calculate how many spaces the number is tot he left of zero on a number line. This number is a distance from zero and will not be negative. All absolute values are positive.
Therefore, the absolute value—or distance from zero—is the following:
Which of the following is equivalent to ?
Which of the following is equivalent to
Tap to see back →
Recall that when a number is raised to an exponent, that means we will need to multiply the number the number of times that is equal to the exponent.
Thus, with , this means we will need to multiply by itself four times:
Recall that when a number is raised to an exponent, that means we will need to multiply the number the number of times that is equal to the exponent.
Thus, with
What is the greatest common factor of and ?
What is the greatest common factor of
Tap to see back →
Start by listing out the factors of .
Next, list out the factors of .
Now, find the largest factor that the two numbers share. In this case, the greatest common factor is .
Start by listing out the factors of
Next, list out the factors of
Now, find the largest factor that the two numbers share. In this case, the greatest common factor is
What is the least common multiple of and ?
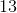What is the least common multiple of
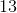
Tap to see back →
Start by listing out multiples of :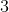
Next, list out multiples of :
Now, find the smallest number that is found in both lists. In this case, the least common multiple must be .
Start by listing out multiples of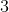
Next, list out multiples of
Now, find the smallest number that is found in both lists. In this case, the least common multiple must be
Give the next number in the sequence:
Give the next number in the sequence:
Tap to see back →
To form the sequence, begin with the term 8. Each subsequent term is equal to 9 added to the previous term, as follows:
,
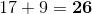
the missing term.
To form the sequence, begin with the term 8. Each subsequent term is equal to 9 added to the previous term, as follows:
the missing term.
Solve for the missing variable in the following proportion:
Solve for the missing variable in the following proportion:
Tap to see back →
Proportions are ratios that are equal to one another. We can solve for the missing variable by using cross multiplication to develop an equation.
Simplify.
Divide both sides of the equation by .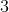
Solve.
Proportions are ratios that are equal to one another. We can solve for the missing variable by using cross multiplication to develop an equation.
Simplify.
Divide both sides of the equation by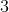
Solve.
Which of the following is equal to six thousand seven ten-thousandths?
Which of the following is equal to six thousand seven ten-thousandths?
Tap to see back →
"Six thousand seven ten-thousandths" in fraction form is . To write this in decimal form, put the "7" in the ten-thousandths place, which is the fourth place after the decimal point. This number is "0.6007."
"Six thousand seven ten-thousandths" in fraction form is
Examine the decimal
What is the place value of the position occupied by the "6"?
Examine the decimal
What is the place value of the position occupied by the "6"?
Tap to see back →
After the decimal point, the place values of the digits are, in order:
...
The "6" is in the fourth place after the decimal point, so its place value is one ten-thousandth.
After the decimal point, the place values of the digits are, in order:
The "6" is in the fourth place after the decimal point, so its place value is one ten-thousandth.
Solve:
Solve:
Tap to see back →
The lines on either side of the negative integer represent that we need to find its absolute value. The absolute value of a number is its real distance from zero on a number line; therefore, we need to calculate how many spaces the number is tot he left of zero on a number line. This number is a distance from zero and will not be negative. All absolute values are positive.
Therefore, the absolute value—or distance from zero—is the following:
The lines on either side of the negative integer represent that we need to find its absolute value. The absolute value of a number is its real distance from zero on a number line; therefore, we need to calculate how many spaces the number is tot he left of zero on a number line. This number is a distance from zero and will not be negative. All absolute values are positive.
Therefore, the absolute value—or distance from zero—is the following:
Which of the following is equivalent to ?
Which of the following is equivalent to
Tap to see back →
Recall that when a number is raised to an exponent, that means we will need to multiply the number the number of times that is equal to the exponent.
Thus, with , this means we will need to multiply by itself four times:
Recall that when a number is raised to an exponent, that means we will need to multiply the number the number of times that is equal to the exponent.
Thus, with
What is the greatest common factor of and ?
What is the greatest common factor of
Tap to see back →
Start by listing out the factors of .
Next, list out the factors of .
Now, find the largest factor that the two numbers share. In this case, the greatest common factor is .
Start by listing out the factors of
Next, list out the factors of
Now, find the largest factor that the two numbers share. In this case, the greatest common factor is
What is the least common multiple of and ?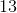
What is the least common multiple of
Tap to see back →
Start by listing out multiples of :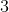
Next, list out multiples of :
Now, find the smallest number that is found in both lists. In this case, the least common multiple must be .
Start by listing out multiples of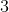
Next, list out multiples of
Now, find the smallest number that is found in both lists. In this case, the least common multiple must be