How to find slope of a line - SSAT Upper Level Quantitative
Card 0 of 84
What is the slope of line 3 = 8y - 4x?
What is the slope of line 3 = 8y - 4x?
Tap to see back →
Solve equation for y. y=mx+b, where m is the slope
Solve equation for y. y=mx+b, where m is the slope
What is the slope of the given linear equation?
2x + 4y = -7
What is the slope of the given linear equation?
2x + 4y = -7
Tap to see back →
We can convert the given equation into slope-intercept form, y=mx+b, where m is the slope. We get y = (-1/2)x + (-7/2)
We can convert the given equation into slope-intercept form, y=mx+b, where m is the slope. We get y = (-1/2)x + (-7/2)
Find the slope of the line 6X – 2Y = 14
Find the slope of the line 6X – 2Y = 14
Tap to see back →
Put the equation in slope-intercept form:
y = mx + b
-2y = -6x +14
y = 3x – 7
The slope of the line is represented by M; therefore the slope of the line is 3.
Put the equation in slope-intercept form:
y = mx + b
-2y = -6x +14
y = 3x – 7
The slope of the line is represented by M; therefore the slope of the line is 3.
What is the slope of the line:
What is the slope of the line:
Tap to see back →
First put the question in slope intercept form (y = mx + b):
–(1/6)y = –(14/3)x – 7 =>
y = 6(14/3)x – 7
y = 28x – 7.
The slope is 28.
First put the question in slope intercept form (y = mx + b):
–(1/6)y = –(14/3)x – 7 =>
y = 6(14/3)x – 7
y = 28x – 7.
The slope is 28.
If 2x – 4y = 10, what is the slope of the line?
If 2x – 4y = 10, what is the slope of the line?
Tap to see back →
First put the equation into slope-intercept form, solving for y: 2x – 4y = 10 → –4y = –2x + 10 → y = 1/2*x – 5/2. So the slope is 1/2.
First put the equation into slope-intercept form, solving for y: 2x – 4y = 10 → –4y = –2x + 10 → y = 1/2*x – 5/2. So the slope is 1/2.
What is the slope of the line with equation 4_x_ – 16_y_ = 24?
What is the slope of the line with equation 4_x_ – 16_y_ = 24?
Tap to see back →
The equation of a line is:
y = mx + b, where m is the slope
4_x_ – 16_y_ = 24
–16_y_ = –4_x_ + 24
y = (–4_x_)/(–16) + 24/(–16)
y = (1/4)x – 1.5
Slope = 1/4
The equation of a line is:
y = mx + b, where m is the slope
4_x_ – 16_y_ = 24
–16_y_ = –4_x_ + 24
y = (–4_x_)/(–16) + 24/(–16)
y = (1/4)x – 1.5
Slope = 1/4
What is the slope of a line which passes through coordinates (3,7) and (4,12)?
What is the slope of a line which passes through coordinates (3,7) and (4,12)?
Tap to see back →
Slope is found by dividing the difference in the y-coordinates by the difference in the x-coordinates.
$\frac{(12-7)}{(4-3)}$=\frac{5}{1}$=5
Slope is found by dividing the difference in the y-coordinates by the difference in the x-coordinates.
$\frac{(12-7)}{(4-3)}$=\frac{5}{1}$=5
What is the slope of a line that passes though the coordinates (5,2) and (3,1)?
What is the slope of a line that passes though the coordinates (5,2) and (3,1)?
Tap to see back →
The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.
Use the give points in this formula to calculate the slope.
The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.
Use the give points in this formula to calculate the slope.
What is the slope of the line represented by the equation 6y-16x=7 ?
What is the slope of the line represented by the equation 6y-16x=7 ?
Tap to see back →
To rearrange the equation into a y=mx+b format, you want to isolate the y so that it is the sole variable, without a coefficient, on one side of the equation.
First, add 11x to both sides to get 6y=7+16x .
Then, divide both sides by 6 to get y=\frac{7+16x}{6}$ .
If you divide each part of the numerator by 6, you get y=\frac{7}{6}$+\frac{16x}{6}$ . This is in a y=b+mx form, and the m is equal to $\frac{16}{6}$, which is reduced down to $\frac{8}{3}$ for the correct answer.
To rearrange the equation into a y=mx+b format, you want to isolate the y so that it is the sole variable, without a coefficient, on one side of the equation.
First, add 11x to both sides to get 6y=7+16x .
Then, divide both sides by 6 to get y=\frac{7+16x}{6}$ .
If you divide each part of the numerator by 6, you get y=\frac{7}{6}$+\frac{16x}{6}$ . This is in a y=b+mx form, and the m is equal to $\frac{16}{6}$, which is reduced down to $\frac{8}{3}$ for the correct answer.
What is the slope of a line running through points 
and 
?
What is the slope of a line running through points
Tap to see back →
The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.
Use the give points in this formula to calculate the slope.
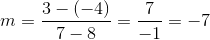
The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.
Use the give points in this formula to calculate the slope.
One end of a board that is four feet long is on the ground. The other end is balanced on a box that is one foot tall, creating a slope. What is the slope of the board?
One end of a board that is four feet long is on the ground. The other end is balanced on a box that is one foot tall, creating a slope. What is the slope of the board?
Tap to see back →
The slope of a line is equal to 
.
Given that the box is one foot tall, the rise will be equal to "1."
Given that the board is four feet long, the run will be equal to "4."
Therefore, the slope is equal to 
.
The slope of a line is equal to
Given that the box is one foot tall, the rise will be equal to "1."
Given that the board is four feet long, the run will be equal to "4."
Therefore, the slope is equal to
A line is given with the equation 
. What is the slope of this line?
A line is given with the equation
Tap to see back →
To find the slope, put the equation in 
form.
Since 
, that must be the slope of the line.
To find the slope, put the equation in
Since
A line goes passes through the points 
. What is the slope of this line?
A line goes passes through the points
Tap to see back →
Use the following formula to find the slope of a line:
The slope of this line would be
Use the following formula to find the slope of a line:
The slope of this line would be
A line has the equation 
. What is the slope of the line?
A line has the equation
Tap to see back →
Change the equation into the more familiar 
form. The value of 
will be the slope.
Change the equation into the more familiar
What is the slope of a line that passes through the points 
?
What is the slope of a line that passes through the points
Tap to see back →
Use the following formula to find the slope:
Plug in the given points to find the slope.
Use the following formula to find the slope:
Plug in the given points to find the slope.
Find the slope of the line that goes through the points 
Find the slope of the line that goes through the points
Tap to see back →
Use the following formula to find the slope:
Plug in the given points to find the slope.
Use the following formula to find the slope:
Plug in the given points to find the slope.
Find the slope of the line that passes through the points 
and 
.
Find the slope of the line that passes through the points
Tap to see back →
Use the following formula to find the slope:
Plug in the given points to find the slope.
Use the following formula to find the slope:
Plug in the given points to find the slope.
Find the slope of the line that passes through the points 
Find the slope of the line that passes through the points
Tap to see back →
Use the following formula to find the slope:
Use the following formula to find the slope:
Find the slope of the line that passes through the points 
Find the slope of the line that passes through the points
Tap to see back →
Use the following formula to find the slope:
Use the following formula to find the slope:
Find the slope of the line that passes through the points 
.
Find the slope of the line that passes through the points
Tap to see back →
Use the following formula to find the slope:
Use the following formula to find the slope: