Interpretation of Tables and Graphs - SSAT Upper Level Quantitative
Card 0 of 100

The above represents a Venn diagram. The universal set  is the set of all positive integers.
is the set of all positive integers.
Let  represent the set of multiples of 7; let
represent the set of multiples of 7; let  represent all of the multiples of 11; let
represent all of the multiples of 11; let  represent all of the multiples of 13. As you can see, the three sets divide the universal set into eight regions. Suppose each positive integer was placed in the correct region. Which of the following numbers would be in the same region as 2,431?
represent all of the multiples of 13. As you can see, the three sets divide the universal set into eight regions. Suppose each positive integer was placed in the correct region. Which of the following numbers would be in the same region as 2,431?

The above represents a Venn diagram. The universal set 
Let 


Tap to see back →
The region in which 2,431 appears depends on the sets of which 2,431 is an element, which in turn depends on which of 7, 11, and 13 divides it evenly:



2,431 is a multiple of 11 and 13, but not 7, so 2,431 is in  and
and  , but not
, but not  . We look for a number among the choices that is in
. We look for a number among the choices that is in  and
and  , but not
, but not  - that is, a number divisible by 11 and 13 but not 7.
- that is, a number divisible by 11 and 13 but not 7.
 , so 2,772 is divisible by 7. We can eliminate it.
, so 2,772 is divisible by 7. We can eliminate it.
 , so 2,184 is divisible by 7. We can eliminate it.
, so 2,184 is divisible by 7. We can eliminate it.
 , so 3,081 is not divisible by 11, and we can eliminate it.
, so 3,081 is not divisible by 11, and we can eliminate it.
 , so 2,409 is not divisible by 13, and we can eliminate it.
, so 2,409 is not divisible by 13, and we can eliminate it.
However:



2,145 is divisible by 11 and 13 but not 7, so this is the correct choice.
The region in which 2,431 appears depends on the sets of which 2,431 is an element, which in turn depends on which of 7, 11, and 13 divides it evenly:
2,431 is a multiple of 11 and 13, but not 7, so 2,431 is in 









However:
2,145 is divisible by 11 and 13 but not 7, so this is the correct choice.
Given the Venn diagram below, which of the following does not belong to  ?
?
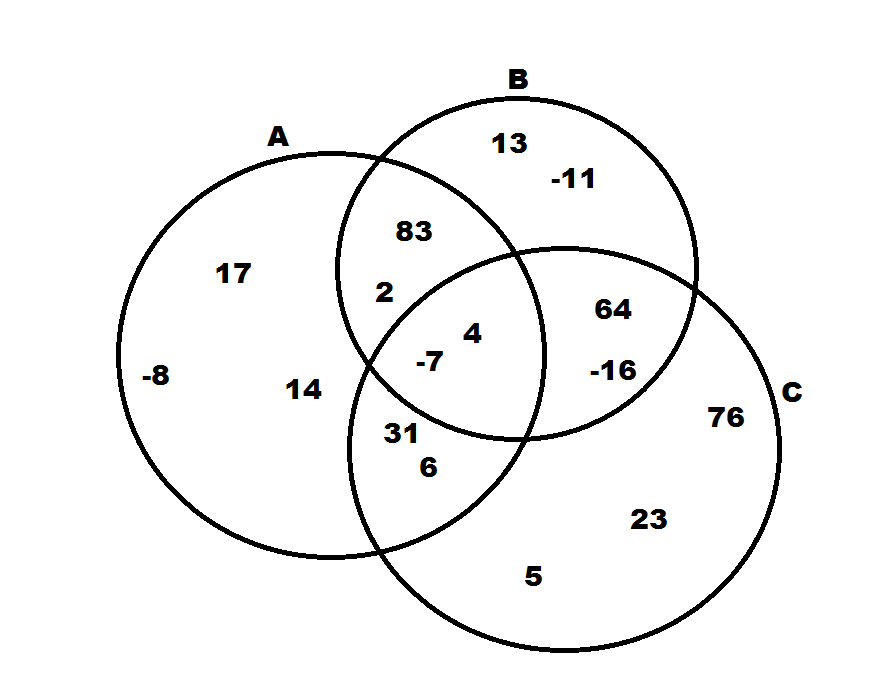
Given the Venn diagram below, which of the following does not belong to 

Tap to see back →
The symbol  stands for the union between two sets. Therefore,
stands for the union between two sets. Therefore,  means the set of all numbers that are in either A or B. Looking at our choices, the only number that isn't in either A, B, or both is 23.
means the set of all numbers that are in either A or B. Looking at our choices, the only number that isn't in either A, B, or both is 23.
The symbol 

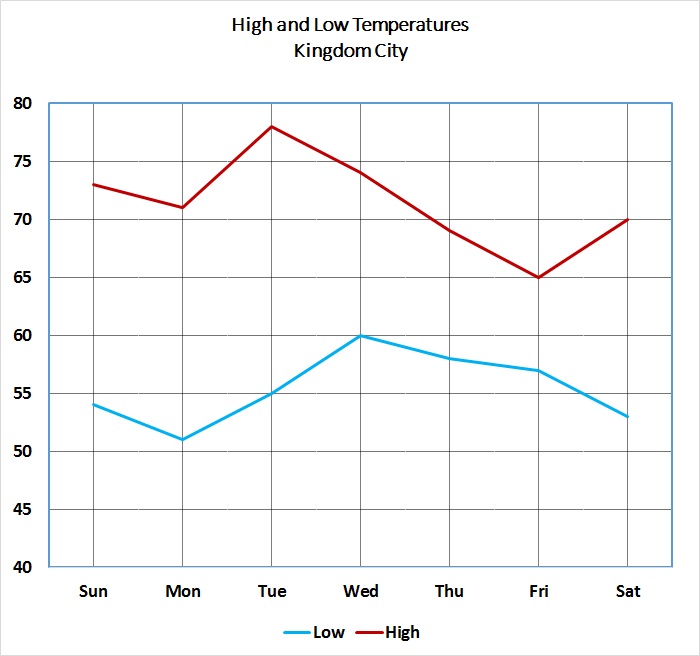
Refer to the above graph, which shows the high and low temperatures for Kingdom City over a one-week period.
Which of the following temperatures occurred at least once on each of the seven days?

Refer to the above graph, which shows the high and low temperatures for Kingdom City over a one-week period.
Which of the following temperatures occurred at least once on each of the seven days?
Tap to see back →
The graph is recreated in the figure below, with horizontal lines at the 57, 62, 67, and 72 degree levels.

It can be seen that of the four lines, only the 62 degree line falls between the high temperature and low temperature for each of the seven days. This is the correct choice.
The graph is recreated in the figure below, with horizontal lines at the 57, 62, 67, and 72 degree levels.

It can be seen that of the four lines, only the 62 degree line falls between the high temperature and low temperature for each of the seven days. This is the correct choice.

The universal set  represented by the above Venn diagram is the set of all natural numbers from
represented by the above Venn diagram is the set of all natural numbers from  to
to  inclusive.
inclusive.
The subsets are:
 : The set of all multiples of
: The set of all multiples of 
 : The set of all multiples of
: The set of all multiples of 
 : The set of all multiples of
: The set of all multiples of 
How many elements are in the set represented by the shaded region?

The universal set 


The subsets are:



How many elements are in the set represented by the shaded region?
Tap to see back →
The shaded region is  , which will comprise all of the numbers that are multiples of 10 and of either or both 8 or 9.
, which will comprise all of the numbers that are multiples of 10 and of either or both 8 or 9.
 will comprise multiples of 10 and 8 - that is, multiples of
will comprise multiples of 10 and 8 - that is, multiples of  . Since
. Since  ,
,

 will comprise multiples of 10 and 9 - that is, multiples of
will comprise multiples of 10 and 9 - that is, multiples of  . Since
. Since  ,
,

To find ![c\left [ \left (A \cap C \right ) \cup \left (B \cap C \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/258895/gif.latex) , we first find
, we first find ![c\left [ \left (A \cap C \right ) \cap \left (B \cap C \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/258896/gif.latex) .
.
 , the set of numbers that are multiples of 8, 9, and 10.
, the set of numbers that are multiples of 8, 9, and 10.  , so we look for multiples of 360, of which there are two under 1,000 (360 and 720).
, so we look for multiples of 360, of which there are two under 1,000 (360 and 720).
![c\left [ \left (A \cap C \right ) \cup \left (B \cap C \right ) \right ] = 2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/265841/gif.latex)
![c\left [ \left (A \cap C \right ) \cup \left (B \cap C \right ) \right ] = c \left (A \cap C \right )+ c \left (B \cap C \right )-c\left [ \left (A \cap C \right ) \cap \left (B \cap C \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/258899/gif.latex)

The shaded region is 






To find ![c\left [ \left (A \cap C \right ) \cup \left (B \cap C \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/258895/gif.latex)
![c\left [ \left (A \cap C \right ) \cap \left (B \cap C \right ) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/258896/gif.latex)



The universal set  represented by the above Venn diagram is the set of all natural numbers from 1 to 1,000 inclusive.
represented by the above Venn diagram is the set of all natural numbers from 1 to 1,000 inclusive.
The subsets are:
 : The set of all multiples of
: The set of all multiples of 
 : The set of all multiples of
: The set of all multiples of 
 : The set of all multiples of
: The set of all multiples of 
How many elements are in the set represented by the shaded region?

The universal set 
The subsets are:



How many elements are in the set represented by the shaded region?
Tap to see back →
The shaded region is inside  and
and  , and outside of
, and outside of  , meaning that the shaded set represents
, meaning that the shaded set represents

Examine  first. Each number in
first. Each number in  must be a multiple of 7 and 8; since the two are relatively prime, each number is a multiple of 56.
must be a multiple of 7 and 8; since the two are relatively prime, each number is a multiple of 56.

so seventeen elements are in  .
.
We eliminate all elements in  - that is, all elements that also multiples of 6. These elements are 168, 336, 504, 672, 840 - a total of five.
- that is, all elements that also multiples of 6. These elements are 168, 336, 504, 672, 840 - a total of five.
This leaves twelve elements in  .
.
The shaded region is inside 


Examine 

so seventeen elements are in 
We eliminate all elements in 
This leaves twelve elements in 

The above Venn diagram represents all of this year's graduating seniors at Rockwell High School, the universal set  .
.
 represents all of the students who are in the National Honor Society.
represents all of the students who are in the National Honor Society.
 represents all of the students who became old enough to vote in the November 5 election during their senior year.
represents all of the students who became old enough to vote in the November 5 election during their senior year.
 represents all of the students who enrolled in a French course during senior year.
represents all of the students who enrolled in a French course during senior year.
Cathy was inducted into the National Honor Society in her junior year, and is still a member. She turned 18 on January 4 during her senior year, and she is carrying a respectable B average in her school's third-year French course. If her name were to be written in the above diagram in the correct place, in which of the five numbered regions would her name fall?

The above Venn diagram represents all of this year's graduating seniors at Rockwell High School, the universal set 



Cathy was inducted into the National Honor Society in her junior year, and is still a member. She turned 18 on January 4 during her senior year, and she is carrying a respectable B average in her school's third-year French course. If her name were to be written in the above diagram in the correct place, in which of the five numbered regions would her name fall?
Tap to see back →
Cathy is in the Honor Society, meaning that she is in set  ; she turned 18 after election day, so she is not in set
; she turned 18 after election day, so she is not in set  ; she is taking a French course, so she is in set
; she is taking a French course, so she is in set  . She is in set
. She is in set  , represented by region 2.
, represented by region 2.
Cathy is in the Honor Society, meaning that she is in set 




In the above Venn diagram, the universal set  is the set of Presidents of the United States.
is the set of Presidents of the United States.
 represents the set of Presidents who were born after 1850.
represents the set of Presidents who were born after 1850.
 represents the set of Presidents who were born in a state completely west of the Mississippi River.
represents the set of Presidents who were born in a state completely west of the Mississippi River.
 represents the set of Presidents who served eight years or more.
represents the set of Presidents who served eight years or more.
Which of the following Presidents would fall in the pink region?

In the above Venn diagram, the universal set 



Which of the following Presidents would fall in the pink region?
Tap to see back →
The shaded region is inside set  , so we are looking for a President who was born after 1850; this eliminates Lincoln.
, so we are looking for a President who was born after 1850; this eliminates Lincoln.
The region is outside of  , so we want a President who served fewer than eight years. This eliminates Wilson and Reagan.
, so we want a President who served fewer than eight years. This eliminates Wilson and Reagan.
The region is outside of  , so we want the state of the President's birth to be fully or partly east of the Mississippi River. This eliminates Nixon.
, so we want the state of the President's birth to be fully or partly east of the Mississippi River. This eliminates Nixon.
The correct response is Harding.
The shaded region is inside set 
The region is outside of 
The region is outside of 
The correct response is Harding.

A group of high school juniors are taking Biology, Calculus, and Spanish as shown above. Which student is not in the set  ?
?

A group of high school juniors are taking Biology, Calculus, and Spanish as shown above. Which student is not in the set 
Tap to see back →
The notation  stands for "union," which refers to everything that is in either set.
stands for "union," which refers to everything that is in either set.  refers to the group of students taking either Calculus or Spanish (everyone on this diagram except those taking only Biology). From the diagram, Patrick and Ashley are the only students taking neither Calculus nor Spanish, so Patrick is the correct answer.
refers to the group of students taking either Calculus or Spanish (everyone on this diagram except those taking only Biology). From the diagram, Patrick and Ashley are the only students taking neither Calculus nor Spanish, so Patrick is the correct answer.
The notation 


The above figure shows two black quarter-circles inscribed inside a rectangle. If the black region has area 200, what is the area of the white region (nearest tenth)?

The above figure shows two black quarter-circles inscribed inside a rectangle. If the black region has area 200, what is the area of the white region (nearest tenth)?
Tap to see back →
If the radius of each quarter-circle is  , the black region has area
, the black region has area

Set  and solve for
and solve for  :
:



The area of the rectangle, which we will call  , is
, is

The area of the white region is the difference of these two areas, or

If the radius of each quarter-circle is 
Set 

The area of the rectangle, which we will call 
The area of the white region is the difference of these two areas, or

Refer to the above graph. Which of the following comes closest to the percent of increase in population enjoyed by Jones City between 1900 and 1950?

Refer to the above graph. Which of the following comes closest to the percent of increase in population enjoyed by Jones City between 1900 and 1950?
Tap to see back →
In 1900, the population was about 3,500; in 1950, it was about 5,600. A reasonable estimate of the percent of increase would be

so 60% would be the most reasonable choice.
In 1900, the population was about 3,500; in 1950, it was about 5,600. A reasonable estimate of the percent of increase would be
so 60% would be the most reasonable choice.

Refer to the above graph, which shows the high and low temperatures for Kingdom City over a one-week period. The temperatures at left are given in degrees Fahrenheit.
Temperatures given in degrees Fahrenheit can be converted to the Celsius scale using the formula
 .
.
Express the lowest temperature of the week in degrees Celsius (nearest whole degree).

Refer to the above graph, which shows the high and low temperatures for Kingdom City over a one-week period. The temperatures at left are given in degrees Fahrenheit.
Temperatures given in degrees Fahrenheit can be converted to the Celsius scale using the formula

Express the lowest temperature of the week in degrees Celsius (nearest whole degree).
Tap to see back →
As can be seen below, the lowest temperature for the week was  , on Monday.
, on Monday.

To convert this to degrees Celsius, set  and substitute in the given formula:
and substitute in the given formula:

 degrees Celsius. The closest choice is
degrees Celsius. The closest choice is  .
.
As can be seen below, the lowest temperature for the week was 

To convert this to degrees Celsius, set 



Refer to the above graph, which shows the high and low temperatures for Kingdom City over a one-week period. The temperatures at left are given in degrees Fahrenheit.
Temperatures given in degrees Fahrenheit can be converted to the Celsius scale using the formula

What was the difference, in degrees Celsius, between the highest temperature and the lowest temperature for the week (to the nearest whole degree)?

Refer to the above graph, which shows the high and low temperatures for Kingdom City over a one-week period. The temperatures at left are given in degrees Fahrenheit.
Temperatures given in degrees Fahrenheit can be converted to the Celsius scale using the formula
What was the difference, in degrees Celsius, between the highest temperature and the lowest temperature for the week (to the nearest whole degree)?
Tap to see back →
As can be seen below, the highest temperature for the week was  , on Tuesday; the low temperature,
, on Tuesday; the low temperature,  , on Monday.
, on Monday.

To convert the former to degrees Celsius, set  and substitute in the given formula:
and substitute in the given formula:

 .
.
To convert the latter, do the same, with  .
.
 .
.
The difference is
 , which rounds to
, which rounds to  .
.
As can be seen below, the highest temperature for the week was 


To convert the former to degrees Celsius, set 

To convert the latter, do the same, with 

The difference is



Refer to the above graph, which shows the high and low temperatures for Kingdom City over a one-week period.
Tim wants to know the high temperature for the Sunday of the next week. He does not have access to that information, but he knows that it was higher than those of exactly four of the five previous days, and lower than that of one of them. Which of the following temperatures could have been the high temperature for that day?

Refer to the above graph, which shows the high and low temperatures for Kingdom City over a one-week period.
Tim wants to know the high temperature for the Sunday of the next week. He does not have access to that information, but he knows that it was higher than those of exactly four of the five previous days, and lower than that of one of them. Which of the following temperatures could have been the high temperature for that day?
Tap to see back →
Since we are dealing with the day after the last one shown, and we are comparing that day's high temperature to those of the previous five days, we only need to concern ourselves with the high temperatures for Tuesday through Saturday.
Examine the figure below, which shows the high temperature line for those five days.

For the high temperature for the next Sunday to be greater than exactly four of the five and less than the remaining one, the temperature must be strictly between the highest and second-highest high temperatures, which are seen to be 78 and 74 degrees, respectively. That is, if we let  be the temperature in degrees,
be the temperature in degrees,

Of the four choices, only 75 falls in this range.
Since we are dealing with the day after the last one shown, and we are comparing that day's high temperature to those of the previous five days, we only need to concern ourselves with the high temperatures for Tuesday through Saturday.
Examine the figure below, which shows the high temperature line for those five days.

For the high temperature for the next Sunday to be greater than exactly four of the five and less than the remaining one, the temperature must be strictly between the highest and second-highest high temperatures, which are seen to be 78 and 74 degrees, respectively. That is, if we let 
Of the four choices, only 75 falls in this range.
The menu of a local coffeehouse reads as follows:

A boss is treating his employees to drinks. Seven of them want iced tea, five want cafe latte, four want espresso, three want cappucino, one wants Americano, and one wants Turkish coffee. How much will the boss spend, disregarding tax?
The menu of a local coffeehouse reads as follows:
A boss is treating his employees to drinks. Seven of them want iced tea, five want cafe latte, four want espresso, three want cappucino, one wants Americano, and one wants Turkish coffee. How much will the boss spend, disregarding tax?
Tap to see back →
Multiply each price by the quantity ordered:
Seven iced teas:

Five cafe lattes:

Four espressos:

Three cappucinos:

Add the $2.39 for the Americano and the $2.09 for the Turkish coffee. The sum:

Multiply each price by the quantity ordered:
Seven iced teas:
Five cafe lattes:
Four espressos:
Three cappucinos:
Add the $2.39 for the Americano and the $2.09 for the Turkish coffee. The sum:

The above is an annual income tax table for married couples for a given state.
Mr. Phillips earned $27,287 last year; Mrs. Phillips earned $25,879. How much will the couple pay in income tax for that year (nearest hundred dollars)?

The above is an annual income tax table for married couples for a given state.
Mr. Phillips earned $27,287 last year; Mrs. Phillips earned $25,879. How much will the couple pay in income tax for that year (nearest hundred dollars)?
Tap to see back →
The Phillips's income totaled
 .
.
This puts them in the 1.3% tax bracket, so they will pay
 in taxes.
in taxes.
The correct response is $700.
The Phillips's income totaled

This puts them in the 1.3% tax bracket, so they will pay

The correct response is $700.

The above is an annual income tax table for single persons in a given state.
Michael earned  per month over a one-year period in his regular job. He also claimed
per month over a one-year period in his regular job. He also claimed  in interest income and
in interest income and  in stock dividends. Based on the above table, which of the following comes closest to the amount of income tax he will pay?
in stock dividends. Based on the above table, which of the following comes closest to the amount of income tax he will pay?

The above is an annual income tax table for single persons in a given state.
Michael earned 


Tap to see back →
From salary, interest, and dividends, Michael earned
 ,
,
putting him in the 1.3% tax bracket.
His income tax will be

making $500 the correct response.
From salary, interest, and dividends, Michael earned

putting him in the 1.3% tax bracket.
His income tax will be
making $500 the correct response.

The above is an annual income tax table for single persons in a given state.
Grant earned $4,389 per month over a one-year period in his regular job. He also claimed $1,736 in interest income and $3,781 in stock dividends. Based on the above table, how much income tax will he pay (nearest dollar)?

The above is an annual income tax table for single persons in a given state.
Grant earned $4,389 per month over a one-year period in his regular job. He also claimed $1,736 in interest income and $3,781 in stock dividends. Based on the above table, how much income tax will he pay (nearest dollar)?
Tap to see back →
Grant earned, in salary, interest, and dividends:

This puts him in the $40-60,000 range, so he will pay $210 plus 1.3% of his income above $40,000. This will be




Grant earned, in salary, interest, and dividends:
This puts him in the $40-60,000 range, so he will pay $210 plus 1.3% of his income above $40,000. This will be

The above is an annual income tax table for married couples for a given state.
Mr. Clarke earned a monthly salary of  throughout last year; Mrs. Clarke earned a monthly salary of
throughout last year; Mrs. Clarke earned a monthly salary of  , although she started on April 1. Also the couple claimed interest earnings of
, although she started on April 1. Also the couple claimed interest earnings of  and
and  in stock dividends. How much will the couple pay in income tax for that year (nearest dollar)?
in stock dividends. How much will the couple pay in income tax for that year (nearest dollar)?

The above is an annual income tax table for married couples for a given state.
Mr. Clarke earned a monthly salary of 



Tap to see back →
Mr. and Mrs. Clarke earned a total of

(noting that Mrs. Clarke worked for nine months)


This places them in the highest tax bracket, so they will pay $810 plus 2.3% of their income over $80,000:




Round this to $2,756.
Mr. and Mrs. Clarke earned a total of
(noting that Mrs. Clarke worked for nine months)
This places them in the highest tax bracket, so they will pay $810 plus 2.3% of their income over $80,000:
Round this to $2,756.

The above is an annual income tax table for single persons in a given state.
Mr. Wells, a single man, paid $690 in taxes last year. Which of the following amounts comes closest to his income for the year?

The above is an annual income tax table for single persons in a given state.
Mr. Wells, a single man, paid $690 in taxes last year. Which of the following amounts comes closest to his income for the year?
Tap to see back →
Since he paid between $470 and $810, his earnings had to have been in the $60,000 to $80,000 range.
Let  be his earnings; then, since he paid $470 plus 1.7% of his income in excess of $60,000, which is equal to $690, we can set up and solve the equation:
be his earnings; then, since he paid $470 plus 1.7% of his income in excess of $60,000, which is equal to $690, we can set up and solve the equation:





The correct choice is $75,000.
Since he paid between $470 and $810, his earnings had to have been in the $60,000 to $80,000 range.
Let 
The correct choice is $75,000.
Column1 Column2 1 0 2 0 3 2 4 3 5 4 6 5 7 8 8 8 9 8 10 8 11 5 12 0
Looking the the table given above, what is the range of the data set?
| Column1 | Column2 |
|---|---|
| 1 | 0 |
| 2 | 0 |
| 3 | 2 |
| 4 | 3 |
| 5 | 4 |
| 6 | 5 |
| 7 | 8 |
| 8 | 8 |
| 9 | 8 |
| 10 | 8 |
| 11 | 5 |
| 12 | 0 |
Looking the the table given above, what is the range of the data set?
Tap to see back →
The range of the data is the difference between the highest and lowest independent variable values.
In this set, the lowest is  and the highest is
and the highest is  .
.
The difference between these two is  .
.
The range of the data is the difference between the highest and lowest independent variable values.
In this set, the lowest is 

The difference between these two is 