Well Orderings and Transfinite Induction - Set Theory
Card 0 of 4
Determine if the following statement is true or false:
Let  and
and 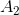 be well ordered and order isomorphic sets. If
be well ordered and order isomorphic sets. If  and
and 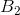 are also order isomorphic sets, then
are also order isomorphic sets, then  and
and  are also order isomorphic.
are also order isomorphic.
Determine if the following statement is true or false:
Let 
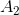

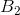


This is a theorem for well ordered sets and the proof is as follows.
First identify what is given in the statement.
1. The sets are onto order isomorphisms
 and
and 
2. The goal is to make an onto order isomorphism. Let us call it  .
.

Thus,  can be defined as the function,
can be defined as the function,

To show  is a well defined, one-to-one, function on
is a well defined, one-to-one, function on  since
since  and
and  are one-to-one, the following is performed.
are one-to-one, the following is performed.


Thus,  is one-to-one.
is one-to-one.
Now to prove  in onto
in onto 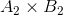 if
if 

for some

thus

proving  is onto
is onto  .
.
Lastly prove ordering.


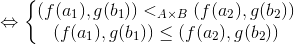
Thus proving  is isomorphic. Therefore the statement is true.
is isomorphic. Therefore the statement is true.
This is a theorem for well ordered sets and the proof is as follows.
First identify what is given in the statement.
1. The sets are onto order isomorphisms

2. The goal is to make an onto order isomorphism. Let us call it 
Thus, 
To show 



Thus, 
Now to prove 
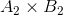
for some
thus
proving 

Lastly prove ordering.
Thus proving 
Compare your answer with the correct one above
Determine if the following statement is true or false:
Let  and
and 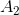 be well ordered and order isomorphic sets. If
be well ordered and order isomorphic sets. If  and
and 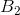 are also order isomorphic sets, then
are also order isomorphic sets, then  and
and  are also order isomorphic.
are also order isomorphic.
Determine if the following statement is true or false:
Let 
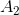

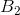


This is a theorem for well ordered sets and the proof is as follows.
First identify what is given in the statement.
1. The sets are onto order isomorphisms
 and
and 
2. The goal is to make an onto order isomorphism. Let us call it  .
.

Thus,  can be defined as the function,
can be defined as the function,

To show  is a well defined, one-to-one, function on
is a well defined, one-to-one, function on  since
since  and
and  are one-to-one, the following is performed.
are one-to-one, the following is performed.


Thus,  is one-to-one.
is one-to-one.
Now to prove  in onto
in onto 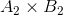 if
if 

for some

thus

proving  is onto
is onto  .
.
Lastly prove ordering.


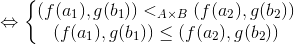
Thus proving  is isomorphic. Therefore the statement is true.
is isomorphic. Therefore the statement is true.
This is a theorem for well ordered sets and the proof is as follows.
First identify what is given in the statement.
1. The sets are onto order isomorphisms

2. The goal is to make an onto order isomorphism. Let us call it 
Thus, 
To show 



Thus, 
Now to prove 
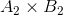
for some
thus
proving 

Lastly prove ordering.
Thus proving 
Compare your answer with the correct one above
Determine if the following statement is true or false:
Let  and
and 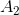 be well ordered and order isomorphic sets. If
be well ordered and order isomorphic sets. If  and
and 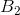 are also order isomorphic sets, then
are also order isomorphic sets, then  and
and  are also order isomorphic.
are also order isomorphic.
Determine if the following statement is true or false:
Let 
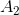

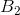


This is a theorem for well ordered sets and the proof is as follows.
First identify what is given in the statement.
1. The sets are onto order isomorphisms
 and
and 
2. The goal is to make an onto order isomorphism. Let us call it  .
.

Thus,  can be defined as the function,
can be defined as the function,

To show  is a well defined, one-to-one, function on
is a well defined, one-to-one, function on  since
since  and
and  are one-to-one, the following is performed.
are one-to-one, the following is performed.


Thus,  is one-to-one.
is one-to-one.
Now to prove  in onto
in onto 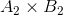 if
if 

for some

thus

proving  is onto
is onto  .
.
Lastly prove ordering.


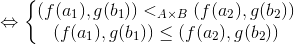
Thus proving  is isomorphic. Therefore the statement is true.
is isomorphic. Therefore the statement is true.
This is a theorem for well ordered sets and the proof is as follows.
First identify what is given in the statement.
1. The sets are onto order isomorphisms

2. The goal is to make an onto order isomorphism. Let us call it 
Thus, 
To show 



Thus, 
Now to prove 
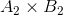
for some
thus
proving 

Lastly prove ordering.
Thus proving 
Compare your answer with the correct one above
Determine if the following statement is true or false:
Let  and
and 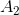 be well ordered and order isomorphic sets. If
be well ordered and order isomorphic sets. If  and
and 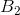 are also order isomorphic sets, then
are also order isomorphic sets, then  and
and  are also order isomorphic.
are also order isomorphic.
Determine if the following statement is true or false:
Let 
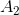

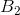


This is a theorem for well ordered sets and the proof is as follows.
First identify what is given in the statement.
1. The sets are onto order isomorphisms
 and
and 
2. The goal is to make an onto order isomorphism. Let us call it  .
.

Thus,  can be defined as the function,
can be defined as the function,

To show  is a well defined, one-to-one, function on
is a well defined, one-to-one, function on  since
since  and
and  are one-to-one, the following is performed.
are one-to-one, the following is performed.


Thus,  is one-to-one.
is one-to-one.
Now to prove  in onto
in onto 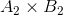 if
if 

for some

thus

proving  is onto
is onto  .
.
Lastly prove ordering.


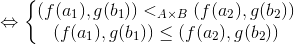
Thus proving  is isomorphic. Therefore the statement is true.
is isomorphic. Therefore the statement is true.
This is a theorem for well ordered sets and the proof is as follows.
First identify what is given in the statement.
1. The sets are onto order isomorphisms

2. The goal is to make an onto order isomorphism. Let us call it 
Thus, 
To show 



Thus, 
Now to prove 
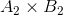
for some
thus
proving 

Lastly prove ordering.
Thus proving 
Compare your answer with the correct one above