Probability
Help Questions
SAT Math › Probability
A box has 4 red and 6 black pens. Two pens are drawn at random without replacement. What is the probability that both pens are red?
$16/100$
$4/10$
$2/15$
$7/10$
Explanation
Without replacement: $(4/10)\cdot(3/9) = 12/90 = 2/15$. The distractors use with-replacement $(4/10)\cdot(4/10)$, ignore the second draw, or add instead of multiply.
A fair six-sided die is rolled once. What is the probability that the result is greater than 4?
$1/2$
$1/3$
$2/3$
$1/6$
Explanation
Outcomes greater than 4 are 5 and 6, so the probability is $2/6 = 1/3$. The other options count the wrong number of favorable or total outcomes.
A box contains 5 red balls and 3 blue balls. If one ball is drawn at random, what is the probability that it is a red ball?
$\frac{5}{16}$
$\frac{3}{8}$
$\frac{5}{8}$
$\frac{1}{2}$
Explanation
This question asks for the probability of drawing a red ball from a box containing red and blue balls. The favorable outcomes are the 5 red balls, and the total possible outcomes are all 8 balls (5 red + 3 blue). Using the probability formula P(red) = favorable outcomes / total outcomes = 5/8.
In a class of 30 students, 18 have a dog, 12 have a cat, and 5 have both a dog and a cat. What is the probability that a student has a dog or a cat?
$\frac{11}{15}$
$\frac{5}{6}$
$\frac{3}{5}$
$\frac{23}{30}$
Explanation
This question asks for the probability that a student has a dog OR a cat, which requires using the addition principle for overlapping events. P(dog or cat) = P(dog) + P(cat) - P(both) = (18 + 12 - 5)/30 = 25/30 = 5/6.
what is the probability that a student is enrolled in at least one of the courses?
0.60
0.70
0.80
0.90
Explanation
This question asks for the probability that a student is enrolled in at least one course (math or science). We have P(math) = 0.60, P(science) = 0.50, and P(both) = 0.30. Using the addition rule: P(at least one) = P(math) + P(science) - P(both) = 0.60 + 0.50 - 0.30 = 0.80. A typical mistake would be adding the percentages without subtracting the overlap, giving 1.10. Remember that 'at least one' means the union of events, requiring careful handling of any overlap between the sets.
A basketball team’s current roster consists of $g$ guards and $f$ forwards. If 2 guards join and 1 forward leaves, what is the probability that a player chosen at random is a guard?
$\frac{g}{g+f}$
$\frac{g+2}{g+f}$
$\frac{g+}{g+f+2}$
$\frac{g+2}{g+f+1}$
Explanation
To find the chances of picking a guard, our formula should be the number of guards divided by the total number of players. We start with $g$ guards and $f$ forwards, and then add 2 guards and subtract one forward. So after the roster changes, we have $g+2$ guards, and we have $g+2+f-1$ total players. Since the probability of an outcome is the number of options that give you that outcome (guards) divided by the number of total options (all players), our probability is then $\frac{g+2}{g+f+1}$.
The table below shows the distribution of a group of 200 students by grade and club membership.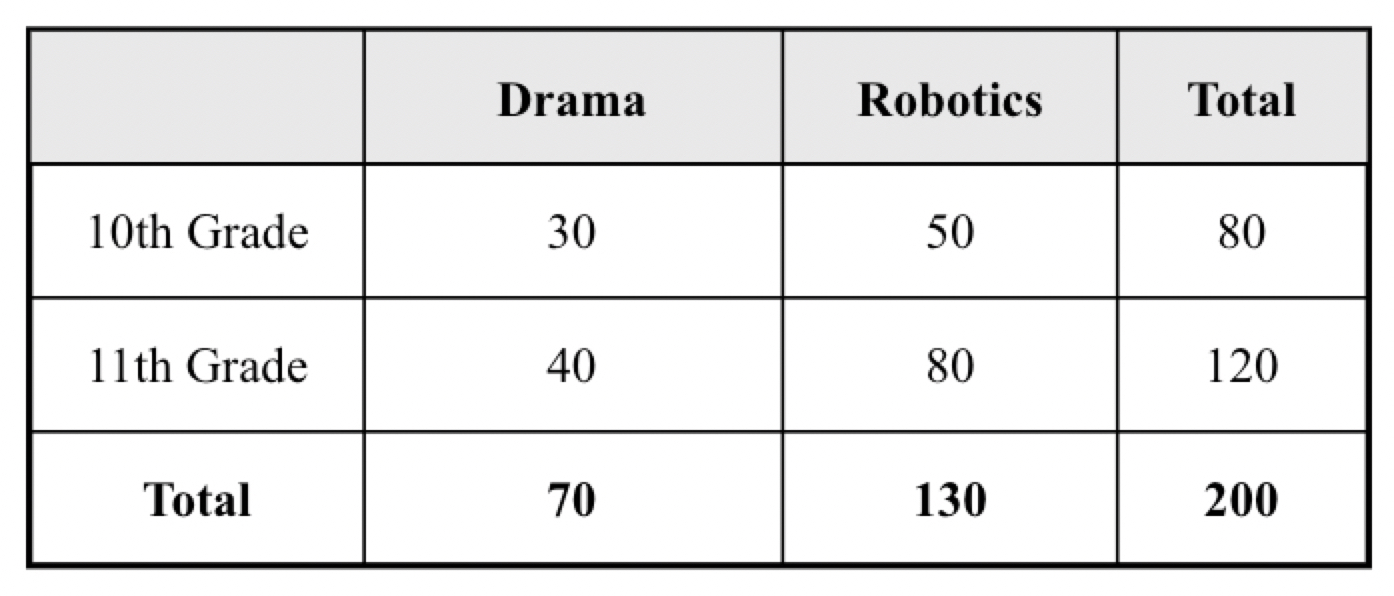
If a student is selected at random from the Robotics club, what is the probability that the student is in 11th Grade?
$\frac{80}{200}$
$\frac{80}{130}$
$\frac{130}{200}$
$\frac{80}{120}$
Explanation
The phrase "from the Robotics club" sets the condition (denominator).
1. Total Robotics students = 130 (Denominator).
2. Target group: 11th Grade students *within* Robotics = 80 (Numerator).
3. Probability = $\frac{80}{130}$.
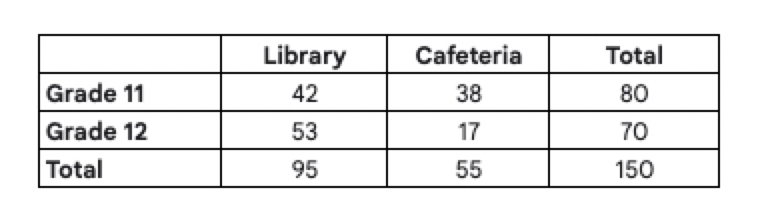
The table below summarizes the results of a survey asking 150 students whether they prefer to study in the library or the cafeteria.
$\frac{53}{150}$
$\frac{53}{70}$
$\frac{95}{150}$
$\frac{53}{95}$
Explanation
This is a conditional probability question. The phrasing "from those who..." establishes a condition that restricts our total sample space.
- Identify the Condition (The Denominator): The question asks to select a student "from those who prefer to study in the library." Looking at the table, the "Total" column for "Library" is $95$. This is our denominator. We ignore the Cafeteria students entirely.
- Identify the Target (The Numerator): From that specific group of $95$ library students, we want to find the number of students in Grade 12. Looking at the intersection of "Library" and "Grade 12", we find $53$ students.
- Form the Fraction: $$P(\text{Grade 12} | \text{Library}) = \frac{\text{Target Group}}{\text{Restricted Total}} = \frac{53}{95}$$
SAT Strategy: Denominator Check
On the SAT, probability questions almost always hinge on reading the denominator correctly.
- If the question says "from the total group," the denominator is $150$.
- If the question says "given the student is in Grade 12," the denominator is $70$.
- Shortcut: Immediately circle the row or column mentioned after the words "given that," "if," or "from those." That circled number is your denominator. In this case, you would circle the "Library" column.