Circles
Help Questions
SAT Math › Circles
Point $P$ lies on the circle $(x-1)^2 + (y-4)^2 = 25$ and has $x$-coordinate $-2$. If $P$ is in Quadrant II, what is the $y$-coordinate of $P$?
0
4
8
16
Explanation
Plugging in $x=-2$ gives $(-3)^2+(y-4)^2=25\Rightarrow(y-4)^2=16\Rightarrow y=0$ or $8$. Quadrant II requires $y>0$, so $y=8$; 0 is the other intersection, and 16/4 are common errors.
A sector of this circle has arc length $15\pi$ units. What is the central angle of the sector, in degrees?
150
$\frac{5}{6}$
$150\pi$
$\frac{5\pi}{6}$
Explanation
From $324\pi=\pi r^2$, $r=18$. The central angle in radians is $\theta=s/r=\frac{15\pi}{18}=\frac{5\pi}{6}$, which is 150 degrees; other choices keep radians or misuse $\pi$.
Circle O has radius 8. The central angle ∠AOB measures $\frac{\pi}{4}$ radians. What is the area of sector AOB?
8
$2\pi$
$16\pi$
$8\pi$
Explanation
Sector area (radians) is $\tfrac{1}{2}r^2\theta = \tfrac{1}{2}\cdot 64 \cdot \tfrac{\pi}{4} = 8\pi$. Choice B omits the $\tfrac{1}{2}$, C computes arc length $r\theta$, and D omits $\pi$.
The circle $x^2 + y^2 = 25$ is centered at the origin. Point B lies on the circle with $x=3$ and has a positive $y$-coordinate. What is $y$?
4
5
6
7
Explanation
From $x^2 + y^2 = 25$, $y^2 = 25 - 9 = 16$, so $y=\pm 4$ and the positive value is 4. The distractors use the radius directly, exceed the radius, or ignore the relationship.
The circle given by $,(x-2)^2 + (y+3)^2 = 36,$ has radius 6. A sector has a central angle of 120°. What is the area of this sector?
12
$12\pi$
$48\pi$
2160
Explanation
Sector area is $\frac{120}{360}\cdot\pi\cdot 6^2 = 12\pi$. Choice A uses the diameter in place of the radius, B omits $\pi$, and D treats 120 as radians.
In a circle with center O and radius 8, the central angle ∠AOB measures $\frac{3\pi}{4}$ radians. What is the length of arc AB?
$12\pi$
$6\pi$
6
$24\pi$
Explanation
With radians, arc length is $s = r\theta = 8\cdot \frac{3\pi}{4} = 6\pi$. Choice A uses the diameter instead of the radius, B omits $\pi$, and D suggests using the full circumference.
The equation of a circle is $(x-3)^2 + (y+4)^2 = 25$. What is the radius of the circle?
3
5
7
25
Explanation
This question asks for the radius of a circle given its equation in standard form. The standard form of a circle equation is (x-h)² + (y-k)² = r², where (h,k) is the center and r is the radius. In the equation (x-3)² + (y+4)² = 25, we can see that r² = 25. Taking the square root of both sides: r = √25 = 5.
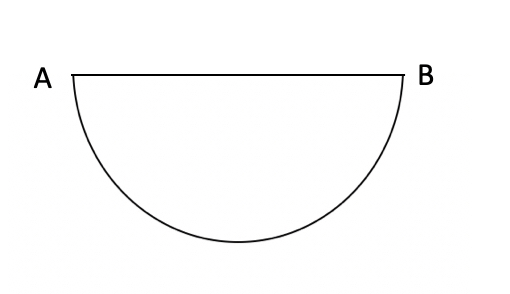
The area of the semicircle above is $32\pi$. What is the length of the arc connecting points A and B?
$16\pi$
$32\pi$
$8\pi$
$4\pi$
Explanation
This problem puts a slight twist on the area of a circle formula, $A=\pi r^2$ You’re given the area of half a circle as $32\pi$, so to apply the area formula you should double $32\pi$ to account for the missing half of the circle so you can use the classic area formula. Since the area of the entire circle would be $64\pi$, you can use the area formula to solve for the radius:
$64\pi = \pi r^2$
$64=r^2$
$8=r$
So the radius is 8, which means you’re ready to apply the formula for circumference of a circle. But again, you’re only dealing with half the circumference since the problem asks for the arc length of the semicircle, so while the formula for circumference is $C=2\pi r$, you can cut that in half to find the distance of half the circumference. That means you need to calculate $\pi r$. With a radius of 8, that means that your answer is $8\pi$
The equation of a circle in the $xy$-plane is shown below.
$$ x^2 + y^2 - 6x + 4y = 12 $$
What is the radius of the circle?
5
12
13
25
Explanation
We must complete the square to put the equation in standard form: $(x-h)^2 + (y-k)^2 = r^2$.
1. Group terms: $(x^2 - 6x) + (y^2 + 4y) = 12$.
2. Complete the square for x: Add $(-6/2)^2 = 9$.
3. Complete the square for y: Add $(4/2)^2 = 4$.
4. Balance the equation: $(x^2 - 6x + 9) + (y^2 + 4y + 4) = 12 + 9 + 4$.
5. Simplify: $(x - 3)^2 + (y + 2)^2 = 25$.
6. $r^2 = 25$, so $r = 5$.
SAT Strategy: Use The Calculator
Note that when you're given an equation and you may not understand it or anticipate that working with it is a lot of work (completing the square often is), another viable strategy is to just plug the equation into Desmos or your graphing calculator. Here if you do that, you'll see a graph of the circle and can click on two points on its diameter to get that length, then divide in two to get the radius.
In the figure above, AC is the diameter of a circle with center O. If the area of the circle is $81\pi$, what is the length of minor arc BC?
$6\pi$
$3.5\pi$
$9\pi$
$7.5\pi$
Explanation
o calculate an arc length, such as the length of minor arc BC here, your job is to find the proportion that that arc represents out of the total circumference. So you'll need to find 1) the circumference and 2) the measure of the central angle of that arc.
Here since you know that the area is $81\pi$, you can use the formula $Area=\pi r^2$ to determine that the radius measures 9.
Then you can plug in that radius into the circumference formula,$Circumference=2 \pi r$, to find that the circumference measures $18\pi$
From this point, you need to find the measure of angle BOC. Since angle AOC measures 180 degrees (you know that it's a straight line, because it's defined as a diameter), and angle AOB = 110, that means that BOC measures 70 degrees. So minor arc BC will be 70/360 of the total circumference, setting up the calculation:
$\frac{70}{360}(18 \pi)$
That reduces to $\frac{7}{2} \pi$ which equals $3.5 \pi$.