Word Translations & Equation Interpretation - SAT Math
Card 0 of 240
The following equation represents the growth of bacteria in a petri dish:  . Which of the following statements best describes this function?
. Which of the following statements best describes this function?
The following equation represents the growth of bacteria in a petri dish: 
The correct answer is “This relationship is exponential and doubles every hour.” Since the time variable  is an exponent, we can narrow down our options and definitively state the function is exponential. The
is an exponent, we can narrow down our options and definitively state the function is exponential. The  is an exponent with a base of
is an exponent with a base of  , so as
, so as  grows, the number of times
grows, the number of times  is multiplied by itself also grows. Each multiplication of two is a doubling of the previous hour’s population (when
is multiplied by itself also grows. Each multiplication of two is a doubling of the previous hour’s population (when  ,
,  vs. when
vs. when  ,
,  ).
).
The correct answer is “This relationship is exponential and doubles every hour.” Since the time variable 








Compare your answer with the correct one above
Which of the following is true about the following function in regards to time  in hours:
in hours:  ?
?
I) This is a linear function
II) When  ,
,  .
.
III) After  hours,
hours,  .
.
Which of the following is true about the following function in regards to time 

I) This is a linear function
II) When 

III) After 

The correct answer is II. This is an exponential function, not a linear function. When we plug in  for
for  ,
,  . When we plug in
. When we plug in  for
for  ,
,  , not
, not  .
.
The correct answer is II. This is an exponential function, not a linear function. When we plug in 






Compare your answer with the correct one above
Maria has a fruit farm and wants to measure her apple and peach harvest from 2000 to 2020. Her apple harvest grew by approximately  bushels per year while her peach harvest grew by
bushels per year while her peach harvest grew by  bushels every
bushels every  years. In 2003, her apple yield was
years. In 2003, her apple yield was  bushels while her peach harvest was
bushels while her peach harvest was  bushels. What is the best estimate for the difference between apple and peach harvests in 2018?
bushels. What is the best estimate for the difference between apple and peach harvests in 2018?
Maria has a fruit farm and wants to measure her apple and peach harvest from 2000 to 2020. Her apple harvest grew by approximately 




The correct answer is  . Maria’s apple harvest follows an exponential pattern while her peach harvest is linear. Since time is relative to any given start point, we can call 2003 the year where
. Maria’s apple harvest follows an exponential pattern while her peach harvest is linear. Since time is relative to any given start point, we can call 2003 the year where  . Her apple harvest *grows* by
. Her apple harvest *grows* by  so when we convert our percent back to a decimal, we get an exponent base of
so when we convert our percent back to a decimal, we get an exponent base of  . Recall, that if her harvest was *losing*
. Recall, that if her harvest was *losing*  of produce yearly, we would use
of produce yearly, we would use  . Since her starting harvest in 2003 was
. Since her starting harvest in 2003 was  bushels, we can model her total bushel count as a function of time through the following equation:
bushels, we can model her total bushel count as a function of time through the following equation:  .
.
Her peach harvest is a linear function that grows by  bushels every
bushels every  years. Since time is measured in single years and our growth is given in periods of
years. Since time is measured in single years and our growth is given in periods of  years, be sure to take this into account in your linear equation
years, be sure to take this into account in your linear equation  . Since her starting harvest in 2003 was
. Since her starting harvest in 2003 was  bushels, we can model her total bushel count as a function of time through the following equation:
bushels, we can model her total bushel count as a function of time through the following equation:  .
.
When we plug  into our equation from subtracting 2003 from 2018, we get
into our equation from subtracting 2003 from 2018, we get  bushels of apples and
bushels of apples and  bushels of peaches.
bushels of peaches.  .
.
The correct answer is 







Her peach harvest is a linear function that grows by 





When we plug 



Compare your answer with the correct one above
The following equation represents the change of a company’s market value since 1993:  . Which of the following statements best describes this function?
. Which of the following statements best describes this function?
The following equation represents the change of a company’s market value since 1993: 
The correct answer is “This company is exponentially shrinking by  .” The above function is an exponential function of t because
.” The above function is an exponential function of t because  is an exponent of a base in the function. A linear equation would utilize
is an exponent of a base in the function. A linear equation would utilize  as a coefficient, not an exponent. The best way to differentiate between growth and shrinkage in an exponential function is to see if the exponent’s base is greater or less than
as a coefficient, not an exponent. The best way to differentiate between growth and shrinkage in an exponential function is to see if the exponent’s base is greater or less than  . If the base is
. If the base is  , there would be no change in
, there would be no change in  regardless of the value of
regardless of the value of  , but if the base is less than
, but if the base is less than  , the company’s value is decreasing.
, the company’s value is decreasing.  so a loss of
so a loss of  of market value annually.
of market value annually.
The correct answer is “This company is exponentially shrinking by 









Compare your answer with the correct one above

The above table shows the growth of two plants in cm. Which of the following statements best describes the growth of these two plants?

The above table shows the growth of two plants in cm. Which of the following statements best describes the growth of these two plants?
The correct answer is “Plant A shows exponential growth while Plant B is linear.” Each hour doubles the height of Plant A. Doubling is a characteristic of exponential growth  . Each hour adds
. Each hour adds  cm to the height of Plant B. Additive and subtractive trends are characteristic of linear growth
cm to the height of Plant B. Additive and subtractive trends are characteristic of linear growth  .
.
The correct answer is “Plant A shows exponential growth while Plant B is linear.” Each hour doubles the height of Plant A. Doubling is a characteristic of exponential growth 


Compare your answer with the correct one above

Which of the following equations most closely describes the above graph?

Which of the following equations most closely describes the above graph?
The correct answer is  . The graph is curved and does not have a defined slope, so it cannot be a linear function
. The graph is curved and does not have a defined slope, so it cannot be a linear function  . Now, between our exponential functions, we can see that at
. Now, between our exponential functions, we can see that at  ,
,  , so this must be a coefficient outside of the exponential base. This only leaves
, so this must be a coefficient outside of the exponential base. This only leaves  . It might be one’s first thought to see that at
. It might be one’s first thought to see that at  ,
,  , pointing to the
, pointing to the  choice, but this equation does not work at any other value of
choice, but this equation does not work at any other value of  .
.
The correct answer is 








Compare your answer with the correct one above

Which of the following sets of equations accurately describes the above graph?


Which of the following sets of equations accurately describes the above graph?

Both exponential equations should represent curved lines while the linear equations should be straight lines.  shows exponential growth, so as
shows exponential growth, so as  increases,
increases,  should increase.
should increase.  shows exponential decay, so as
shows exponential decay, so as  increases,
increases,  should decrease. This narrows us down to Option 2 and 4. Within the linear equations,
should decrease. This narrows us down to Option 2 and 4. Within the linear equations,  should be a steeper line than
should be a steeper line than  since the slope is greater, thus leaving us with Option 4 as the correct answer.
since the slope is greater, thus leaving us with Option 4 as the correct answer.
Both exponential equations should represent curved lines while the linear equations should be straight lines. 







Compare your answer with the correct one above
The population of moths in a given forest has been decreasing by  every
every  years since 2004. The population at the beginning of 2004 was
years since 2004. The population at the beginning of 2004 was  . If
. If  represents the total moth population at time
represents the total moth population at time  years after 2004, which following equations most closely describes the total moth population at any given time?
years after 2004, which following equations most closely describes the total moth population at any given time?
The population of moths in a given forest has been decreasing by 




Since the total moth population is a percentage of the previous period’s population, we know this is an exponential function and not a linear one. We also know that the population has been decreasing. An exponent base of  would represent no change in the population, while a base of less than one would represent a decrease, so this rules out the option with
would represent no change in the population, while a base of less than one would represent a decrease, so this rules out the option with  as the exponent base. The population has been decreasing by
as the exponent base. The population has been decreasing by  so we can say the original
so we can say the original  of the population loses
of the population loses  , leaving us with
, leaving us with  of the original population for every
of the original population for every  years that pass. Also, we use
years that pass. Also, we use  because the population only decreases by
because the population only decreases by  every
every  years. This leaves us with
years. This leaves us with  .
.
Since the total moth population is a percentage of the previous period’s population, we know this is an exponential function and not a linear one. We also know that the population has been decreasing. An exponent base of 










Compare your answer with the correct one above
Which of the following statements are true about an exponential function?
I) It takes the form 
II) It changes at a constant rate per unit interval
III) It changes by a common ratio over equal intervals
Which of the following statements are true about an exponential function?
I) It takes the form
II) It changes at a constant rate per unit interval
III) It changes by a common ratio over equal intervals
Exponential functions are in the form  while linear are
while linear are  . Linear functions change at a constant rate per unit interval while exponential functions change by a common ratio over equal intervals.
. Linear functions change at a constant rate per unit interval while exponential functions change by a common ratio over equal intervals.
Exponential functions are in the form 

Compare your answer with the correct one above
Which of the following statements are true about the exponential function:  ?
?
I) The y-intercept of this graph is 
II) The base in this equation is 
III) The x-intercept of this equation is 
Which of the following statements are true about the exponential function: 
I) The y-intercept of this graph is
II) The base in this equation is
III) The x-intercept of this equation is
When  (the y-intercept),
(the y-intercept),  . The base of this equation is
. The base of this equation is  . Exponential functions never have x-intercepts unless they are in the form
. Exponential functions never have x-intercepts unless they are in the form  .
.
When 



Compare your answer with the correct one above

Archaeologists use the equation above to estimate the height of fossil hominids from the length of their femurs. If  represents the estimated height, in centimeters, and
represents the estimated height, in centimeters, and  represents the measured femur length, in centimeters, what is role of the humber
represents the measured femur length, in centimeters, what is role of the humber  in the equation?
in the equation?
Archaeologists use the equation above to estimate the height of fossil hominids from the length of their femurs. If 


Note that in this equation, the number 54.1 is a constant: it isn't multiplied by anything. So 54.1 is a minimum number: a femur cannot have a minimum length, so even if  were to equal zero, the estimated height would be 54.1. This tells you that 54.1 has to be the absolute minimum estimated height of a hominid using this method.
were to equal zero, the estimated height would be 54.1. This tells you that 54.1 has to be the absolute minimum estimated height of a hominid using this method.
Note that in this equation, the number 54.1 is a constant: it isn't multiplied by anything. So 54.1 is a minimum number: a femur cannot have a minimum length, so even if 
Compare your answer with the correct one above
In preparation for wrestling tryouts, Trey sets a goal of doing 270 pushups per week. The number of pushups he has remaining for the week can be expressed at the end of each day by the equation  , where
, where  is the number of pushups and
is the number of pushups and  is the number of days he has completed his pushups that week. What is the meaning of the value 45 in this equation?
is the number of days he has completed his pushups that week. What is the meaning of the value 45 in this equation?
In preparation for wrestling tryouts, Trey sets a goal of doing 270 pushups per week. The number of pushups he has remaining for the week can be expressed at the end of each day by the equation 


Remember: in word problems, units are always important! In this problem, thinking about units is a great place to start. Since you know that P is a number of pushups, then the other side of the equation needs to be a number of pushups, too, so that the units match. And three of the four items in the equation are given to you:
P = Number of pushups left
270 = Total number of pushups
d = Days that Trey has done pushups
That alone helps you use process of elimination, since "number of days he's already done pushups" and "number of pushups remaining" are already defined by other parts of the equation. And it should also help you think your way through it. Without using the test’s variables, you could set up your own equation:
Pushups left = Total - Pushups he’s already done
And since “pushups he’s already done” is represented mathematically as 45d, you can eliminate that answer since 45 itself doesn’t equal that overall value – it needs to be multiplied by d. Or, as before, you can look at the 45d portion as a recurring amount. d = the number of days, and if you multiply the number of days by the number of pushups per day, you’ll get the total amount of pushups over that period. So 45 is the number of pushups that he does each day.
Remember: in word problems, units are always important! In this problem, thinking about units is a great place to start. Since you know that P is a number of pushups, then the other side of the equation needs to be a number of pushups, too, so that the units match. And three of the four items in the equation are given to you:
P = Number of pushups left
270 = Total number of pushups
d = Days that Trey has done pushups
That alone helps you use process of elimination, since "number of days he's already done pushups" and "number of pushups remaining" are already defined by other parts of the equation. And it should also help you think your way through it. Without using the test’s variables, you could set up your own equation:
Pushups left = Total - Pushups he’s already done
And since “pushups he’s already done” is represented mathematically as 45d, you can eliminate that answer since 45 itself doesn’t equal that overall value – it needs to be multiplied by d. Or, as before, you can look at the 45d portion as a recurring amount. d = the number of days, and if you multiply the number of days by the number of pushups per day, you’ll get the total amount of pushups over that period. So 45 is the number of pushups that he does each day.
Compare your answer with the correct one above
A taxi service calculates its fares using the formula  , where
, where  is the total fare and
is the total fare and  is the total number of miles of the trip. Which of the following best describes the role of the number 2.50?
is the total number of miles of the trip. Which of the following best describes the role of the number 2.50?
A taxi service calculates its fares using the formula 


Notice that the number 2.50 isn’t multiplied by anything, so it’s not a recurring charge of any kind. Even if m = 0, that 2.50 remains unchanged, so 2.50 is the charge that happens regardless of the distance. This tells you that 2.50 is the up-front fee that is charged regardless of the number of miles on the trip.
Notice that the number 2.50 isn’t multiplied by anything, so it’s not a recurring charge of any kind. Even if m = 0, that 2.50 remains unchanged, so 2.50 is the charge that happens regardless of the distance. This tells you that 2.50 is the up-front fee that is charged regardless of the number of miles on the trip.
Compare your answer with the correct one above
A beekeeper models the number of bees in his colony by the equation  , where
, where  represents the number of bees in the colony and
represents the number of bees in the colony and  represents the number of months since he began his colony. Based on the model, which of the following statements are true?
represents the number of months since he began his colony. Based on the model, which of the following statements are true?
I. The number of bees in the colony is decreasing with time.
II. The colony began with over 200 bees.
III. The colony gains an average of 8 bees per year.
A beekeeper models the number of bees in his colony by the equation 


I. The number of bees in the colony is decreasing with time.
II. The colony began with over 200 bees.
III. The colony gains an average of 8 bees per year.
On occasion, the SAT will present you with problems like this one, in which you have to determine what must be true for up to three different statements. These tend to be a bit more time consuming, because they’re essentially three problems in one.
Looking at the given equation,  , analyze the role of each term.
, analyze the role of each term.
 is the total number of bees at any given point of time.
is the total number of bees at any given point of time.
 says that for every month, the number of bees increases by approximately 2/3 (note that this is the beekeeper's model, not an exact number, so it's okay that the number of bees isn't always an integer)
says that for every month, the number of bees increases by approximately 2/3 (note that this is the beekeeper's model, not an exact number, so it's okay that the number of bees isn't always an integer)
 is a constant, and if
is a constant, and if  were 0 the total number of bees would be 212. So this must mean that there were 212 bees to start.
were 0 the total number of bees would be 212. So this must mean that there were 212 bees to start.
If you then look at the statements:
I is not true, as the number of bees is increasing with each month.
II is true; the beginning number was 212.
III is true; if the number of bees grows by 2/3 each month, and there are 12 months in a year, then the number of bees is growing by an estimated 8 bees each year.
On occasion, the SAT will present you with problems like this one, in which you have to determine what must be true for up to three different statements. These tend to be a bit more time consuming, because they’re essentially three problems in one.
Looking at the given equation, 




If you then look at the statements:
I is not true, as the number of bees is increasing with each month.
II is true; the beginning number was 212.
III is true; if the number of bees grows by 2/3 each month, and there are 12 months in a year, then the number of bees is growing by an estimated 8 bees each year.
Compare your answer with the correct one above
Hannah is selling candles for a school fundraiser all fall. She sets a goal of selling  candles per month. The number of candles she has remaining for the month can be expressed at the end of each week by the equations
candles per month. The number of candles she has remaining for the month can be expressed at the end of each week by the equations  , where
, where  is the number of candles and
is the number of candles and  is the number of weeks she has sold candles this month. What is the meaning of the value
is the number of weeks she has sold candles this month. What is the meaning of the value  in this equation?
in this equation?
Hannah is selling candles for a school fundraiser all fall. She sets a goal of selling 




Since we know that  stands for weeks, the answer has to have something to do with the weeks. This eliminates "the number of candles she has remaining for the month." Also, we can eliminate "the number of weeks that she has sold candles this month" because that would be our value for
stands for weeks, the answer has to have something to do with the weeks. This eliminates "the number of candles she has remaining for the month." Also, we can eliminate "the number of weeks that she has sold candles this month" because that would be our value for  , not what we'd multiply
, not what we'd multiply  by. The correct answer is, "the number of candles that she sells each week."
by. The correct answer is, "the number of candles that she sells each week."
Since we know that 


Compare your answer with the correct one above
Upon discovering a tree virus in British Columbia, scientists created a model to predict the tree population in a certain forest:  , where
, where  represents he number of trees after
represents he number of trees after  months since the virus's discovery, and
months since the virus's discovery, and  represents the original number of trees that existed in the forest when the scientists made the discovery. Assuming that the model is correct, which of the following best describes the impact of the virus on the forest?
represents the original number of trees that existed in the forest when the scientists made the discovery. Assuming that the model is correct, which of the following best describes the impact of the virus on the forest?
Upon discovering a tree virus in British Columbia, scientists created a model to predict the tree population in a certain forest: 



As you can see from the answer choices to the first question, you need to make two important determinations:
- Is this an exponential decrease, or a linear decrease?
- Should the number in question be 73 or 27?
When you’re determining whether a change is exponential or linear, look to see if there is an exponent. The exponent,
 , just outside the parentheses tells you that this is an exponential function. What does that mean? That the loss of 27% per month compounds each month. Exponential increases and decreases mean that the increase or decrease is taken as a percent of the new value each time; linear increases and decreases mean that the same amount is increased or decreased each month, because that percent change is taken from the original value. So this is an exponential change, meaning that the answer must be one of the percentages, not one of the numbers.
, just outside the parentheses tells you that this is an exponential function. What does that mean? That the loss of 27% per month compounds each month. Exponential increases and decreases mean that the increase or decrease is taken as a percent of the new value each time; linear increases and decreases mean that the same amount is increased or decreased each month, because that percent change is taken from the original value. So this is an exponential change, meaning that the answer must be one of the percentages, not one of the numbers.
The fact that this is a decrease tells you what is happening inside the parentheses. For an exponential decrease, the formula is:
New value = (Original Value)(1 - rate)(number of periods)
The rate is a percentage expressed as a decimal, and in a decrease problem that rate is always subtracted from 1. This is because you’re calculating the number of items (in this case trees) remaining, so you need to convert the decrease into a function of the number that you keep, not the number that you’re losing. Think of it like a discount at a store: if an item is 20% off, you pay the other 80% of the price that’s remaining. So here, the expression shows that 73% of the trees remain each month, meaning that the forest is losing 27% of its trees each month (1−0.27=0.73). Therefore, the correct answer is "the number of trees is decreasing by 27% each month."
As you can see from the answer choices to the first question, you need to make two important determinations:
- Is this an exponential decrease, or a linear decrease?
- Should the number in question be 73 or 27?
When you’re determining whether a change is exponential or linear, look to see if there is an exponent. The exponent,
, just outside the parentheses tells you that this is an exponential function. What does that mean? That the loss of 27% per month compounds each month. Exponential increases and decreases mean that the increase or decrease is taken as a percent of the new value each time; linear increases and decreases mean that the same amount is increased or decreased each month, because that percent change is taken from the original value. So this is an exponential change, meaning that the answer must be one of the percentages, not one of the numbers.
The fact that this is a decrease tells you what is happening inside the parentheses. For an exponential decrease, the formula is:
New value = (Original Value)(1 - rate)(number of periods)
The rate is a percentage expressed as a decimal, and in a decrease problem that rate is always subtracted from 1. This is because you’re calculating the number of items (in this case trees) remaining, so you need to convert the decrease into a function of the number that you keep, not the number that you’re losing. Think of it like a discount at a store: if an item is 20% off, you pay the other 80% of the price that’s remaining. So here, the expression shows that 73% of the trees remain each month, meaning that the forest is losing 27% of its trees each month (1−0.27=0.73). Therefore, the correct answer is "the number of trees is decreasing by 27% each month."
Compare your answer with the correct one above
Shawn is purchasing t-shirts for himself and the members of his soccer team. The online vendor uses the formula  to represent the total cost a customer pays, inclusive of the price of each shirt plus a one-time shipping fee that is the same regardless of the number of shirts purchased. If
to represent the total cost a customer pays, inclusive of the price of each shirt plus a one-time shipping fee that is the same regardless of the number of shirts purchased. If  represents the total amount that Shawn will pay for purchasing
represents the total amount that Shawn will pay for purchasing  shirts, what is the role of the number
shirts, what is the role of the number  in this formula?
in this formula?
Shawn is purchasing t-shirts for himself and the members of his soccer team. The online vendor uses the formula 



When you see formulas like this that express the total cost for a number of items, there are some standard components you should recognize. Whenever there is a plain number added, with no variable next to it (as you see with + 10 here), that is a fixed charge that does not depend on the number of items purchased. Where you do see a number multiplied by a variable, like with 12s here, that represents the amount of money that depends on the number of items purchased: the numerical coefficient is the cost-per-item, and the variable is the number of items. Which should make logical sense - the shopper gets to choose the number of items to buy, so that number can vary customer to customer, making a "variable" appropriate there. Here you're asked about the number 12, which is multiplied by the variable s - that means that 12 is the price per shirt, with s being the number of shirts Shawn purchases.
When you see formulas like this that express the total cost for a number of items, there are some standard components you should recognize. Whenever there is a plain number added, with no variable next to it (as you see with + 10 here), that is a fixed charge that does not depend on the number of items purchased. Where you do see a number multiplied by a variable, like with 12s here, that represents the amount of money that depends on the number of items purchased: the numerical coefficient is the cost-per-item, and the variable is the number of items. Which should make logical sense - the shopper gets to choose the number of items to buy, so that number can vary customer to customer, making a "variable" appropriate there. Here you're asked about the number 12, which is multiplied by the variable s - that means that 12 is the price per shirt, with s being the number of shirts Shawn purchases.
Compare your answer with the correct one above
A pizzeria uses the equation  to predict the number of pizzas,
to predict the number of pizzas,  , that will be ordered for delivery in any given hour based on the number of football games,
, that will be ordered for delivery in any given hour based on the number of football games,  , that are being televised during that hour. What is the meaning of the value
, that are being televised during that hour. What is the meaning of the value  in this equation?
in this equation?
A pizzeria uses the equation 



In this equation you know that  is the total number of pizzas and that
is the total number of pizzas and that  is the number of football games. Think about what happens: if
is the number of football games. Think about what happens: if  increases, there are more pizzas ordered.
increases, there are more pizzas ordered.  tells us how many extra pizzas are ordered for each game that is being televised. The pizzeria would sell 10 pizzas if no games were on TV, 13 if one is on, 16 if two is on, etc. So
tells us how many extra pizzas are ordered for each game that is being televised. The pizzeria would sell 10 pizzas if no games were on TV, 13 if one is on, 16 if two is on, etc. So  is the number of additional pizzas expected to be ordered per football game on TV.
is the number of additional pizzas expected to be ordered per football game on TV.
In this equation you know that 




Compare your answer with the correct one above
Researchers have modeled the extent of ice loss in Greenland using the equation  , where
, where  represents the surface area of Greenland covered by ice, in square kilometers, measured on September 30 of each year,
represents the surface area of Greenland covered by ice, in square kilometers, measured on September 30 of each year,  represents the 12.8% rate at which ice is lost each year, and
represents the 12.8% rate at which ice is lost each year, and  represents the number of years that have elapsed since the study began in 1979. What is the meaning of the number
represents the number of years that have elapsed since the study began in 1979. What is the meaning of the number  in this equation?
in this equation?
Researchers have modeled the extent of ice loss in Greenland using the equation 




An exponential change calculation generally has three components: the initial amount, the percent change, and the number of periods that have undergone that change. The typical structure of such a calculation is:
New Amount = Original Amount(1 +/- Percent Change As A Decimal)Number of Periods
Here we're dealing with a 12.8% decrease, so within the parentheses the percentage is subtracted, and  has been identified as the number of periods.
has been identified as the number of periods.  is the original amount that gets multiplied by the percent change taken to its exponent, so the correct answer is the original amount, which in this problem is defined as "The number of square kilometers of ice in Greenland as of September 30, 1979."
is the original amount that gets multiplied by the percent change taken to its exponent, so the correct answer is the original amount, which in this problem is defined as "The number of square kilometers of ice in Greenland as of September 30, 1979."
An exponential change calculation generally has three components: the initial amount, the percent change, and the number of periods that have undergone that change. The typical structure of such a calculation is:
New Amount = Original Amount(1 +/- Percent Change As A Decimal)Number of Periods
Here we're dealing with a 12.8% decrease, so within the parentheses the percentage is subtracted, and 

Compare your answer with the correct one above
Sarah has created an equation to model the amount of money in her savings account. Her net income is \$50,000 per year, and her expenses each month are \$2,000, so she models her savings at the end of each month using the equation:

In this equation, 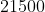 represents the \$21,500 she had in savings when she first began tracking her savings this way, and
represents the \$21,500 she had in savings when she first began tracking her savings this way, and  represents the number of months that it has been since she started. What is the meaning of the number
represents the number of months that it has been since she started. What is the meaning of the number  in this calculation?
in this calculation?
Sarah has created an equation to model the amount of money in her savings account. Her net income is \$50,000 per year, and her expenses each month are \$2,000, so she models her savings at the end of each month using the equation:
In this equation, 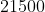


In this problem, Sarah's income is quoted as an annual amount but her expenses are quoted as a monthly amount. In order to calculate her savings, she needs those units to both be in either "per year" or "per month." Since the variable  also represents a number of months, it is necessary for her to convert her annual salary into a monthly amount so that she can properly subtract expenses from income to reflect the amount of money saved. Therefore, dividing by 12 is how she makes that conversion.
also represents a number of months, it is necessary for her to convert her annual salary into a monthly amount so that she can properly subtract expenses from income to reflect the amount of money saved. Therefore, dividing by 12 is how she makes that conversion.
In this problem, Sarah's income is quoted as an annual amount but her expenses are quoted as a monthly amount. In order to calculate her savings, she needs those units to both be in either "per year" or "per month." Since the variable 
Compare your answer with the correct one above





 , just outside the parentheses tells you that this is an exponential function. What does that mean? That the loss of 27% per month compounds each month. Exponential increases and decreases mean that the increase or decrease is taken as a percent of the new value each time; linear increases and decreases mean that the same amount is increased or decreased each month, because that percent change is taken from the original value. So this is an exponential change, meaning that the answer must be one of the percentages, not one of the numbers.
, just outside the parentheses tells you that this is an exponential function. What does that mean? That the loss of 27% per month compounds each month. Exponential increases and decreases mean that the increase or decrease is taken as a percent of the new value each time; linear increases and decreases mean that the same amount is increased or decreased each month, because that percent change is taken from the original value. So this is an exponential change, meaning that the answer must be one of the percentages, not one of the numbers.