Fractions - SAT Math

Card 0 of 1832

Question

Simplify:

Answer

Division is the same as multiplying by the reciprocal. Thus, a/b ÷ c/d = a/b x d/c = ad/bc

Compare your answer with the correct one above

Question

If p is a positive integer, and 4 is the remainder when p-8 is divided by 5, which of the following could be the value of p?

Answer

Remember that if x has a remainder of 4 when divided by 5, xminus 4 must be divisible by 5. We are therefore looking for a number p such that p - 8 - 4 is divisible by 5. The only answer choice that fits this description is 17.

Compare your answer with the correct one above

Question

If $\dpi{100} \small x=\frac{2}{3}$ and $\dpi{100} \small y= \frac {3}{4}$ , then what is the value of $\dpi{100} \small \frac {x}{y}$ ?

Answer

Dividing by a number (in this case $\dpi{100} \small \frac {3}{4}$ ) is equivalent to multiplying by its reciprocal (in this case $\dpi{100} \small \frac {4}{3}$ ). Therefore:

$\dpi{100} \small \frac {2}{3}\div \frac{3}{4} = \frac{2}{3}\times \frac{4}{3} = \frac{8}{9}$

Compare your answer with the correct one above

Question

Evaluate the following:

$\left ( \frac{5}{6}\times \frac{12}{13} \right )^{2}\div \frac{3}{4}$

Answer

$\left ( \frac{5}{6}\times \frac{12}{13} \right )^{2}\div \frac{3}{4}$

First we will evaluate the terms in the parentheses:

$\left ( \frac{5}{6}\times \frac{2\times 6}{13} \right )^{2}\div \frac{3}{4}$

$\left ( \frac{5}{1}\times \frac{2}{13} \right )^{2}\div \frac{3}{4}$

$\left ( \frac{10}{13} \right )^{2}\div \frac{3}{4}$

Next, we will square the first fraction:

$\left ( \frac{10^{2}}{13^{2}} \right )\div \frac{3}{4}$

$\frac{100}{169}\div \frac{3}{4}$

We can evaluate the division as such:

$\frac{100}{169}\times\frac{4}{3}=\frac{400}{507}$

Compare your answer with the correct one above

Question

Evaluate the expression:

$\frac{3}{9}\div \frac{4}{15}$

Answer

When dividing fractions, you invert the second term and multiply the numbers.

$\frac{3}{9}\times\frac{15}{4}$

You can reduce the numbers that are diagonal from each other to make the numbers smaller and easier to multiply.

$\frac{3}{3}\times\frac{5}{4}=\frac{5}{4}=1\frac{1}{4}$

Compare your answer with the correct one above

Question

Simplify $\frac{\frac{13x}{5y}}{\frac{3x}{8y}}$

Answer

When you dividing fractions, multiply by the reciprocal of the denominator.

$\frac{\frac{13x}{5y}}{\frac{3x}{8y}}=\frac{13x}{5y}\frac{8y}{3x}=\frac{13x8y}{5y3x}=\frac{138}{5*3}=\frac{104}{15}$

Compare your answer with the correct one above

Question

A TV show lasts 30 minutes, what fraction of the show is left after 12 minutes have passed?

Answer

After watching 12 minutes of the show 18 remain. 18 is 60% of the total 30 minutes. As a fraction it can be expressed as 3/5.

Compare your answer with the correct one above

Question

A bag contains red, orange, and yellow marbles only. The marbles occur in a ratio of 5 red marbles: 4 orange marbles: 1 yellow marble. If one-third of the red marbles, one-half of the orange marbles, and one-fourth of the yellow marbles are removed, then what fraction of the remaining marbles in the bag is red?

Answer

Compare your answer with the correct one above

Question

Marty drove 40 mi/hr for 3 hours, then 60 mi/hr for 1 hour, and finally 70 mi/hr for the last 2 hours. What was Marty's average speed?

Answer

Marty's total driving time was 3 + 1 + 2 = 6 hours. He drove 40 mi/hr for 3 hours, or 3/6 = 1/2 of the time. He drove 60 mi/hr for 1 hour, or 1/6 of the drive. Lastly, he drove 70 mi/hr for 2 hours, or 2/6 = 1/3 of the drive.

To find the average speed, we need to multiply the speeds with their corresponding weights and add them up.

Average = 1/2 * 40 + 1/6 * 60 + 1/3 * 70 = 53.33... ≈ 53 mi/hr

Compare your answer with the correct one above

Question

A pie is made up of $\frac{1}{9}$ crust, $\frac{1}{3}$ apples, and $\frac{1}{4}$ sugar, and the rest is jelly. What is the ratio of crust to jelly?

Answer

A pie is made up of $\frac{1}{9}$ crust, $\frac{1}{3}$ apples, $\frac{1}{4}$ sugar, and the rest is jelly. What is the ratio of crust to jelly?

To compute this ratio, you must first ascertain how much of the pie is jelly. This is:

$1-\frac{1}{4}-\frac{1}{3}-\frac{1}{9}$

Begin by using the common denominator :

$1-\frac{1}{4}-\frac{1}{3}-\frac{1}{9}=\frac{36}{36}-\frac{9}{36}-\frac{12}{36}-\frac{4}{36}$

$\frac{36}{36}-\frac{9}{36}-\frac{12}{36}-\frac{4}{36}=\frac{11}{36}$

So, the ratio of crust to jelly is:

$\frac{1}{9}:\frac{11}{36}$

This can be written as the fraction:

$\frac{\frac{1}{9}}{\frac{11}{36}}=\frac{1}{9}*\frac{36}{11}=\frac{4}{11}$ , or

Compare your answer with the correct one above

Question

In a solution, $\frac{1}{3}$ of the fluid is water, $\frac{1}{5}$ is wine, and $\frac{7}{15}$ is lemon juice. What is the ratio of lemon juice to water?

Answer

This problem is really an easy fraction division. You should first divide the lemon juice amount by the water amount:

$\frac{lemon:juice}{water}=\frac{\frac{7}{15}}{\frac{1}{3}}$

Remember, to divide fractions, you multiply by the reciprocal:

$\frac{\frac{7}{15}}{\frac{1}{3}} = \frac{7}{15}*3=\frac{7}{5}$

This is the same as saying:

Compare your answer with the correct one above

Question

If $x=\frac{11}{100}$ and $y=\frac{15}{8}$ , what is the ratio of to ?

Answer

To find a ratio like this, you simply need to make the fraction that represents the division of the two values by each other. Therefore, we have:

$x:y=\frac{\frac{11}{100}}{\frac{15}{8}}$

Recall that division of fractions requires you to multiply by the reciprocal:

$\frac{\frac{11}{100}}{\frac{15}{8}} = \frac{11}{100}\frac{8}{15}=\frac{11}{25}\frac{2}{15}$ ,

which is the same as:

$\frac{22}{375}$

This is the same as the ratio:

Compare your answer with the correct one above

Question

If Mr. Jones’ math class has 8 boys and two-thirds of the class are girls, how many total students are in the class?

Answer

If two-thirds of the class are girls, then one-third must be boys. Set up an equation comparing the number of boys to how much they represent in the entire class:

8 = (1/3) x, where x is the number in the entire class.

When we solve for x in the equation we get x = 24.

Compare your answer with the correct one above

Question

Mr. Owens spent $7.50 for a dinner buffet. The amount he paid accounted for 3/4 of the money in his wallet. How much money is left in his wallet for other expenses?

Answer

If $7.50 is 3/4 of the total, 7.50/3 gives us what 1/4 of his total money would be. This equals $2.50, the remaining unspent quarter.

Compare your answer with the correct one above

Question

A certain ball that is dropped will bounce back to 3/5 of the height it was initially dropped from. If after the 2nd bounce the ball reaches 39.96 ft, what was the initial height the ball was dropped from?

Answer

We know the height of the initial bounce, so work backwards to find the initial height. 39.96/0.6 = 66.6 = height of ball after first bounce

66.6/0.6 = 111 ft

Compare your answer with the correct one above

Question

A pitcher of water is filled $\dpi{100} \small \frac{2}{5}$ of full. An additional 27 ounces of water is added. Now the pitcher of water is completely full. How much water does the pitcher hold?

Answer

If $\dpi{100} \small 27$ ounces fills the pitcher, then it must equal the volume of $\dpi{100} \small \frac{3}{5}$ of the pitcher. If $\dpi{100} \small \frac{3}{5}$ of a pitcher equals 27 ounces, then $\dpi{100} \small \frac{1}{5}$ of a pitcher equals $\dpi{100} \small 27\div 3=9$ ounces. Since there are $\dpi{100} \small 5$ fifths in the pitcher, it must hold $\dpi{100} \small 9\times 5=45$ ounces total.

Compare your answer with the correct one above

Question

is what of what?

Answer

With the given information, we can set up a proportion.

$\frac{6}{x}=\frac{30}{100}$

Compare your answer with the correct one above

Question

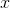If $\frac{1}{3} < x < 0.76$ , can equal which of the following?

Answer

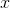
Convert all of the fractions to decimals. Thus, x is contained within the range of 0.33 < x < 0.76. The answers choices become 1/4 = 0.25, 4/12 = 0.33, 2/5 = 0.4, and 5/16 = 0.3125, respectively. Therefore, the only answer which is within the desired range is 2/5.

Compare your answer with the correct one above

Question

What is the reciprocal of the following fraction: 18/27

Answer

A fraction multiplied by its reciprocal will equal 1. To find the reciprocal of a fraction, switch the denominator and numerator. The reciprocal of 18/27 is 27/18.

Compare your answer with the correct one above

Question

What is the reciprocal of the fraction below?

$\frac{2}{9}$

Answer

The reciprocal of a fraction can be obtained by switching the numerator and denominator.

The numerator in this case is so that will become the denominator.

The denominator in this case is so that will become the numerator.

Threfore the reciprocal of $\frac{2}{9}$ is $\frac{9}{2}$ .

Compare your answer with the correct one above

Tap the card to reveal the answer