Basic Squaring / Square Roots - SAT Math
Card 0 of 768
Evaluate: 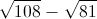
Evaluate:
Let us factor 108 and 81



Let us factor 108 and 81
Compare your answer with the correct one above
Solve for  :
:

Solve for 

Notice how all of the quantities in square roots are divisible by 9






Simplifying, this becomes

Notice how all of the quantities in square roots are divisible by 9
Simplifying, this becomes
Compare your answer with the correct one above
Solve for  :
:

Solve for 
In order to solve for  , first note that all of the square root terms on the left side of the equation have a common factor of 9 and 9 is a perfect square:
, first note that all of the square root terms on the left side of the equation have a common factor of 9 and 9 is a perfect square:



Simplifying, this becomes:




In order to solve for 
Simplifying, this becomes:
Compare your answer with the correct one above
Solve for  :
:

Solve for 

Note that all of the square root terms share a common factor of 36, which itself is a square of 6:


Factoring  from both terms on the left side of the equation:
from both terms on the left side of the equation:



Note that all of the square root terms share a common factor of 36, which itself is a square of 6:
Factoring 
Compare your answer with the correct one above
Solve for  :
:

Solve for 

Note that both  and
and  have a common factor of
have a common factor of  and
and  is a perfect square:
is a perfect square:



From here, we can factor  out of both terms on the lefthand side
out of both terms on the lefthand side




Note that both 



From here, we can factor 
Compare your answer with the correct one above
Which of the following is equivalent to:
 ?
?
Which of the following is equivalent to:

To begin with, factor out the contents of the radicals. This will make answering much easier:

They both have a common factor  . This means that you could rewrite your equation like this:
. This means that you could rewrite your equation like this:

This is the same as:

These have a common  . Therefore, factor that out:
. Therefore, factor that out:

To begin with, factor out the contents of the radicals. This will make answering much easier:
They both have a common factor 
This is the same as:
These have a common 
Compare your answer with the correct one above
Simplify:

Simplify:
These three roots all have a  in common; therefore, you can rewrite them:
in common; therefore, you can rewrite them:

Now, this could be rewritten:

Now, note that 
Therefore, you can simplify again:

Now, that looks messy! Still, if you look carefully, you see that all of your factors have  ; therefore, factor that out:
; therefore, factor that out:

This is the same as:

These three roots all have a 
Now, this could be rewritten:
Now, note that
Therefore, you can simplify again:
Now, that looks messy! Still, if you look carefully, you see that all of your factors have 
This is the same as:
Compare your answer with the correct one above
Solve for  :
:

Solve for 
Examining the terms underneath the radicals, we find that  and
and  have a common factor of
have a common factor of  .
.  itself is a perfect square, being the product of
itself is a perfect square, being the product of  and
and  . Hence, we recognize that the radicals can be re-written in the following manner:
. Hence, we recognize that the radicals can be re-written in the following manner:
 , and
, and  .
.
The equation can then be expressed in terms of these factored radicals as shown:




Factoring the common term  from the lefthand side of this equation yields
from the lefthand side of this equation yields

Divide both sides by the expression in the parentheses:

Divide both sides by  to yield
to yield  by itself on the lefthand side:
by itself on the lefthand side:

Simplify the fraction on the righthand side by dividing the numerator and denominator by  :
:

This is the solution for the unknown variable  that we have been required to find.
that we have been required to find.
Examining the terms underneath the radicals, we find that 







The equation can then be expressed in terms of these factored radicals as shown:
Factoring the common term 
Divide both sides by the expression in the parentheses:
Divide both sides by 

Simplify the fraction on the righthand side by dividing the numerator and denominator by 
This is the solution for the unknown variable 
Compare your answer with the correct one above
Simplify in radical form:

Simplify in radical form:
To simplify, break down each square root into its component factors:



You can remove pairs of factors and bring them outside the square root sign. At this point, since each term shares  , you can add them together to yield the final answer:
, you can add them together to yield the final answer:

To simplify, break down each square root into its component factors:
You can remove pairs of factors and bring them outside the square root sign. At this point, since each term shares 
Compare your answer with the correct one above
Simplify: 
Simplify:
Take each fraction separately first:
(2√3)/(√2) = \[(2√3)/(√2)\] * \[(√2)/(√2)\] = (2 * √3 * √2)/(√2 * √2) = (2 * √6)/2 = √6
Similarly:
(4√2)/(√3) = \[(4√2)/(√3)\] * \[(√3)/(√3)\] = (4√6)/3 = (4/3)√6
Now, add them together:
√6 + (4/3)√6 = (3/3)√6 + (4/3)√6 = (7/3)√6
Take each fraction separately first:
(2√3)/(√2) = \[(2√3)/(√2)\] * \[(√2)/(√2)\] = (2 * √3 * √2)/(√2 * √2) = (2 * √6)/2 = √6
Similarly:
(4√2)/(√3) = \[(4√2)/(√3)\] * \[(√3)/(√3)\] = (4√6)/3 = (4/3)√6
Now, add them together:
√6 + (4/3)√6 = (3/3)√6 + (4/3)√6 = (7/3)√6
Compare your answer with the correct one above
If  what is
what is  ?
?
If 

Square both sides:
x = (32)2 = 92 = 81
Square both sides:
x = (32)2 = 92 = 81
Compare your answer with the correct one above
Simplify the following expression: 
Simplify the following expression:
Begin by factoring out each of the radicals:

For the first two radicals, you can factor out a  or
or  :
:

The other root values cannot be simply broken down. Now, combine the factors with  :
:

This is your simplest form.
Begin by factoring out each of the radicals:
For the first two radicals, you can factor out a 

The other root values cannot be simply broken down. Now, combine the factors with 
This is your simplest form.
Compare your answer with the correct one above
Solve for  .
.
Note,  :
:

Solve for 
Note, 
Begin by getting your  terms onto the left side of the equation and your numeric values onto the right side of the equation:
terms onto the left side of the equation and your numeric values onto the right side of the equation:

Next, you can combine your radicals. You do this merely by subtracting their respective coefficients:

Now, square both sides:



Solve by dividing both sides by  :
:

Begin by getting your 
Next, you can combine your radicals. You do this merely by subtracting their respective coefficients:
Now, square both sides:
Solve by dividing both sides by 
Compare your answer with the correct one above
(√27 + √12) / √3 is equal to
(√27 + √12) / √3 is equal to
√27 is the same as 3√3, while √12 is the same as 2√3.
3√3 + 2√3 = 5√3
(5√3)/(√3) = 5
√27 is the same as 3√3, while √12 is the same as 2√3.
3√3 + 2√3 = 5√3
(5√3)/(√3) = 5
Compare your answer with the correct one above
Simplify: 
Simplify:
When dividing square roots, we divide the numbers inside the radical. Simplify if necessary.

When dividing square roots, we divide the numbers inside the radical. Simplify if necessary.
Compare your answer with the correct one above
Simplify: 
Simplify:
When dividing square roots, we divide the numbers inside the radical. Simplify if necessary.

Let's simplify this even further by factoring out a  .
.

When dividing square roots, we divide the numbers inside the radical. Simplify if necessary.
Let's simplify this even further by factoring out a 
Compare your answer with the correct one above
Simplify: 
Simplify:
When dividing square roots, we divide the numbers inside the radical. Simplify if necessary.

Let's simplify this even further by factoring out a  .
.

When dividing square roots, we divide the numbers inside the radical. Simplify if necessary.
Let's simplify this even further by factoring out a 
Compare your answer with the correct one above
Evaluate: 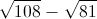
Evaluate:
Let us factor 108 and 81



Let us factor 108 and 81
Compare your answer with the correct one above
How many integers from 20 to 80, inclusive, are NOT the square of another integer?
How many integers from 20 to 80, inclusive, are NOT the square of another integer?
First list all the integers between 20 and 80 that are squares of another integer:
52 = 25
62 = 36
72 = 49
82 = 64
In total, there are 61 integers from 20 to 80, inclusive. 61 – 4 = 57
First list all the integers between 20 and 80 that are squares of another integer:
52 = 25
62 = 36
72 = 49
82 = 64
In total, there are 61 integers from 20 to 80, inclusive. 61 – 4 = 57
Compare your answer with the correct one above
The square root of 5184 is:
The square root of 5184 is:
The easiest way to narrow down a square root from a list is to look at the last number on the squared number – in this case 4 – and compare it to the last number of the answer.
70 * 70 will equal XXX0
71 * 71 will equal XXX1
72 * 72 will equal XXX4
73 * 73 will equal XXX9
74 * 74 will equal XXX(1)6
Therefore 72 is the answer. Check by multiplying it out.
The easiest way to narrow down a square root from a list is to look at the last number on the squared number – in this case 4 – and compare it to the last number of the answer.
70 * 70 will equal XXX0
71 * 71 will equal XXX1
72 * 72 will equal XXX4
73 * 73 will equal XXX9
74 * 74 will equal XXX(1)6
Therefore 72 is the answer. Check by multiplying it out.
Compare your answer with the correct one above