Algebra - SAT Math

Card 0 of 9157

Question

If and are positive integers and , then what is the value of $\frac{m}{n}$ ?

Answer

43 = 64

Alternatively written, this is 4(4)(4) = 64 or 43 = 641.

Thus, m = 3 and n = 1.

m/n = 3/1 = 3.

Compare your answer with the correct one above

Question

Write the following logarithm in expanded form:

$\log x^{2}y$

Answer

$\log x^{2}y=\log x^{2}+\log y=2\log x+\log y$

Compare your answer with the correct one above

Question

If and are both rational numbers and $4^{m} = 8^{n}$ , what is $\frac{m}{n}$ ?

Answer

This question is asking you for the ratio of m to n. To figure it out, the easiest way is to figure out when 4 to an exponent equals 8 to an exponent. The easiest way to do that is to list the first few results of 4 to an exponent and 8 to an exponent and check to see if any match up, before resorting to more drastic means of finding a formula.

$4^{1} = 4, 4^{2} = 16, 4^{3} = 64, 4^{4} = 256, 4^{5} = 1024$

$8^{1}=8, 8^{2} = 64, 8^{3} = 512, 8^{4} = 4096, 8^{5} = 32768$

And, would you look at that. $4^{3}= 8^{2}$ . Therefore, $\frac{m}{n} = \frac{3}{2}$ .

Compare your answer with the correct one above

Question

Subtract from .

Answer

Step 1: We need to read the question carefully. It says subtract from. When you see the word "from", you read the question right to left.

I am subtracting the left equation from the right equation.

Step 2: We need to write the equation on the right minus the equation of the left.

Step 3: Distribute the minus sign in front of the parentheses:

Step 4: Combine like terms:

Step 5: Put all the terms together, starting with highest degree. The degree of the terms is the exponent. Here, the highest degree is 2 and lowest is zero.

The final equation is

Compare your answer with the correct one above

Question

Define an operation $\heartsuit$ on the set of real numbers as follows:

For all real ,

$m \heartsuit n = \left ( m-4n\right )^{3}$

How else could this operation be defined?

Answer

$\left ( m-4n\right )^{3}$ , as the cube of a binomial, can be rewritten using the following pattern:

$\left ( m-4n\right )^{3} = m ^{3} - 3 \cdot m ^{2} \cdot 4n + 3 \cdot m \cdot (4n) ^{2}- (4n) ^{3}$

Applying the rules of exponents to simplify this:

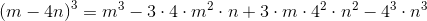
$\left ( m-4n\right )^{3} = m ^{3} - 3 \cdot 4 \cdot m ^{2} \cdot n + 3 \cdot m \cdot 4 ^{2}\cdot n ^{2}- 4^{3} \cdot n ^{3}$

$\left ( m-4n\right )^{3} = m ^{3} - 3 \cdot 4 \cdot m ^{2} \cdot n + 3 \cdot 16 \cdot m\cdot n ^{2}- 4^{3} \cdot n ^{3}$

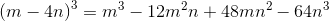
$\left ( m-4n\right )^{3} = m ^{3} -12 m ^{2} n + 48mn ^{2}- 64n ^{3}$

Therefore, the correct choice is that, alternatively stated,

$m \heartsuit n = m ^{3} -12 m ^{2} n + 48mn ^{2}- 64n ^{3}$ .

Compare your answer with the correct one above

Question

Let . What is the following equivalent to, in terms of :

$\frac{x}{\sqrt{y}}$

Answer

Solve for x first in terms of y, and plug back into the equation.

$\4x^2 = y^3 \ \x^2 = \frac{1}{4} y^3 \ \x = \pm \frac{1}{2} y\sqrt{y}$

Then go back to the equation you are solving for:

$\frac{x}{\sqrt{y}}$ substitute in $x=\pm\frac{1}{2}y\sqrt{y}$

$\ \frac{x}{\sqrt{y}}=\frac{\pm\frac{1}{2}y\sqrt{y}}{\sqrt{y}} \ \\frac{x}{\sqrt{y}}=\pm\frac{1}{2}y$

Compare your answer with the correct one above

Question

For which of the following values of is the value of ${x^{-\frac{1}{2}}}$ least?

Answer

${x^{-\frac{1}{2}}}$ is the same as $\frac{1}{\sqrt{x}}$ , which means that the bigger the answer to $\sqrt{x}$ is, the smaller the fraction will be.

Therefore, is the correct answer because

$\frac{1}{\sqrt{16}} = \frac{1}{4}$ .

Compare your answer with the correct one above

Question

Define an operation $\ast$ so that for any two complex numbers and :

$a \ast b = \frac{a + b}{a}$

Evaluate $(2+i) \ast i$ .

Answer

$a \ast b = \frac{a + b}{a}$ , so

$(2+i) \ast i = \frac{(2+ i )+ i}{2+i} = \frac{2 + 2i}{2+i}$

Rationalize the denominator by multiplying both numerator and denominator by the complex conjugate of the latter, which is :

$(2+i) \ast i$

$= \frac{2 + 2i}{2+i}$

$= \frac{\left (2 + 2i \right )\left (2-i \right )}{\left (2+i \right )\left (2-i \right )}$

$= \frac{ 2 \cdot 2 - 2 \cdot i + 2i \cdot 2 - 2i \cdot i}{2 ^{2}+1^{2}}$

$= \frac{ 4 - 2 i + 4i - 2 \cdot i^{2}}{4+1}$

$= \frac{ 4 - 2 i + 4i - 2 \cdot (-1)}{5}$

$= \frac{ 4 - 2 i + 4i +2}{5}$

$= \frac{ 6 + 2 i }{5}$

$= \frac{ 6 }{5} + \frac{ 2 }{5}i$

Compare your answer with the correct one above

Question

Simplify the expression by rationalizing the denominator, and write the result in standard form: $\frac{5+i}{7-i}$

$\left (\textup{Note: } i=\sqrt{-1}\right\ )$

Answer

Multiply both numerator and denominator by the complex conjugate of the denominator, which is :

$\frac{5+i}{7-i}$

$= \frac{(5+i)(7+i)}{(7-i)(7+i)}$

$= \frac{5 \cdot 7 + 5 \cdot i + 7 \cdot i + i \cdot i }{(7^{2}+1 ^{2}) }$

$= \frac{35 +5i + 7 i +(-1) }{(49+1) }$

$= \frac{34 +12i }{50 }$

$= \frac{34 }{50 } + \frac{ 12i }{50 }$

$= \frac{17}{25} + \frac{ 6}{25}i$

Compare your answer with the correct one above

Question

Define an operation $\ast$ so that for any two complex numbers and :

$a \ast b = \frac{a + b}{a}$

Evaluate $(3+2i) \ast 2$

Answer

$a \ast b = \frac{a + b}{a}$ , so

$(3+2i) \ast 2 = \frac{(3+2i) + 2}{3+2i } = \frac{5+2i}{3+2i }$

Rationalize the denominator by multiplying both numerator and denominator by the complex conjugate of the latter, which is :

$(3+2i) \ast 2 = \frac{5+2i}{3+2i }$

$= \frac{\left (5+2i \right )\left (3-2i \right )}{\left (3+2i \right )\left (3-2i \right )}$

$= \frac{5 \cdot 3 - 5 \cdot 2i + 2i \cdot 3 - 2i \cdot 2i }{3^{2}+2^{2}}$

$= \frac{5 \cdot 3 - 5 \cdot 2i + 2i \cdot 3 - 2 \cdot 2 \cdot i^{2} }{9+4}$

$= \frac{15 - 10i + 6i -4 \cdot (-1) }{9+4}$

$= \frac{15 - 10i + 6i +4}{13}$

$= \frac{19 -4i}{13}$

$= \frac{19 }{13} - \frac{ 4}{13}i$

Compare your answer with the correct one above

Question

Define an operation $\Phi$ such that, for any complex number ,

$\Phi a = a + 2ai$

If $\Phi N = i$ , then evaluate .

Answer

$\Phi a = a + 2ai$ , so

$\Phi N = N + 2Ni = N (1+ 2i)$

$\Phi N = i$ , so

, and

$N=\frac{ i}{ 1+ 2i}$

Rationalize the denominator by multiplying both numerator and denominator by the complex conjugate of the latter, which is :

$N=\frac{ i}{ 1+ 2i}$

$=\frac{ i( 1- 2i)}{( 1+ 2i)( 1- 2i)}$

$=\frac{ i \cdot 1- i \cdot 2i}{1 ^{2}+2^{2}}$

$=\frac{ i - 2i^{2}}{1+4}$

$=\frac{ i - 2(-1)}{5}$

$=\frac{ i +2}{5}$

$=\frac{ 2}{5} + \frac{1}{5} i$

Compare your answer with the correct one above

Question

Define an operation $\Theta$ such that for any complex number ,

$\Theta a = 2a i + i$

If $\Theta N = 1,000$ , evaluate .

Answer

First substitute our variable N in where ever there is an a.

Thus, $\Theta a = 2a i + i$ , becomes $\Theta N = 2N i + i$ .

Since $\Theta N = 1,000$ , substitute:

In order to solve for the variable we will need to isolate the variable on one side with all other constants on the other side. To do this, apply the oppisite operation to the function.

First subtract i from both sides.

Now divide by 2i on both sides.

$\frac{2N i}{2i}= \frac{1,000 - i}{2i}$

From here multiply the numerator and denominator by i to further solve.

$N= \frac{1,000 - i}{2i}$

$= \frac{(1,000 - i) \cdot i }{2i \cdot i}$

$= \frac{1,000\cdot i - i\cdot i }{2 \cdot i^{2}}$

Recall that by definition. Therefore,

$= \frac{1,000 i - (-1) }{2 \cdot (-1)}$

$= \frac{1,000 i +1 }{-2}$

$= \frac{ 1 }{-2}+ \frac{1,000 i }{-2}$

$=- \frac{ 1 }{2}- 500i$ .

Compare your answer with the correct one above

Question

Define an operation $\blacklozenge$ as follows:

For any two complex numbers and ,

$a \blacklozenge b = \frac{a}{2i} + \frac{2i}{b}$

Evaluate $(1+ i) \blacklozenge (1+ i)$ .

Answer

$a \blacklozenge b = \frac{a}{2i} + \frac{2i}{b}$ , so

$(1+ i) \blacklozenge (1+ i) = \frac{1+ i}{2i} + \frac{2i}{1+ i}$

We can simplify each expression separately by rationalizing the denominators.

$\frac{1+ i}{2i}$

$= \frac{\left (1+ i \right )\cdot i}{2i \cdot i}$

$= \frac{1 \cdot i+ i \cdot i}{2 \cdot i ^{2}}$

$= \frac{ i+(-1)}{2 (-1)}$

$= \frac{-1+i}{-2}$

$= \frac{ 1 }{2} - \frac{1}{2} i$

$\frac{2i}{1+ i}$

$= \frac{2i(1- i)}{(1+ i)(1- i)}$

$= \frac{2i \cdot 1- 2i \cdot i}{1^{2}+1^{2}}$

$= \frac{2i - 2i ^{2}}{1+1}$

$= \frac{2i - 2(-1)}{2}$

$= \frac{2i +2}{2}$

Therefore,

$(1+ i) \blacklozenge (1+ i) = \frac{1+ i}{2i} + \frac{2i}{1+ i}$

$=\left ( \frac{ 1 }{2} - \frac{1}{2} i \right )+ \left (1 + i \right )$

$=\left ( \frac{ 1 }{2}+1 \right )+ \left ( i- \frac{1}{2} i \right )$

$= \frac{ 3 }{2} + \frac{1}{2} i$

Compare your answer with the correct one above

Question

Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)

Answer

Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.

Compare your answer with the correct one above

Question

Simplify the following rational expression:

$\frac{7x-18}{x^{2}}+\frac{6x-14}{x^{2}}$

Answer

Since both fractions in the expression have a common denominator of $x^{2}$ , we can combine like terms into a single numerator over the denominator:

$\frac{7x-18}{x^{2}}+\frac{6x-14}{x^{2}}$

$=\frac{(7x-18)+(6x-14)}{x^{2}}$

$=\frac{13x-32}{x^{2}}$

Compare your answer with the correct one above

Question

Simplify the following rational expression:

$\frac{5x-5}{2x^{2}} + \frac{7x+9}{2x^{2}}$

Answer

Since both rational terms in the expression have the common denominator $2x^{2}$ , combine the numerators and simplify like terms:

$\frac{5x-5}{2x^{2}} + \frac{7x+9}{2x^{2}}$

$=\frac{(5x-5)+(7x+9)}{2x^{2}}$

$=\frac{12x+4}{2x^{2}}$

$=\frac{6x+2}{x^2}$

Compare your answer with the correct one above

Question

Simplify the following expression:

$\frac{10x-9}{x^{3}}+\frac{11x+12}{x^{3}}$

Answer

Since both terms in the expression have the common denominator $x^{3}$ , combine the fractions and simplify the numerators:

$\frac{10x-9}{x^{3}}+\frac{11x+12}{x^{3}}$

$=\frac{(10x-9)+(11x+12)}{x^{3}}$

$=\frac{21x+3}{x^{3}}$

Compare your answer with the correct one above

Question

Answer

Compare your answer with the correct one above

Question

In the equation below, , , and are non-zero numbers. What is the value of in terms of and ?

$\frac{1}{m^3}-\frac{1}{k^2}=\frac{1}{p}$

Answer

Compare your answer with the correct one above

Question

Answer

Compare your answer with the correct one above

Tap the card to reveal the answer