Circles - PSAT Math
Card 0 of 616
If it is 2:00 PM, what is the measure of the angle between the minute and hour hands of the clock?
If it is 2:00 PM, what is the measure of the angle between the minute and hour hands of the clock?
Tap to see back →
First note that a clock is a circle made of 360 degrees, and that each number represents an angle and the separation between them is 360/12 = 30. And at 2:00, the minute hand is on the 12 and the hour hand is on the 2. The correct answer is 2 * 30 = 60 degrees.
First note that a clock is a circle made of 360 degrees, and that each number represents an angle and the separation between them is 360/12 = 30. And at 2:00, the minute hand is on the 12 and the hour hand is on the 2. The correct answer is 2 * 30 = 60 degrees.
A car tire has a radius of 18 inches. When the tire has made 200 revolutions, how far has the car gone in feet?
A car tire has a radius of 18 inches. When the tire has made 200 revolutions, how far has the car gone in feet?
Tap to see back →
If the radius is 18 inches, the diameter is 3 feet. The circumference of the tire is therefore 3π by C=d(π). After 200 revolutions, the tire and car have gone 3π x 200 = 600π feet.
If the radius is 18 inches, the diameter is 3 feet. The circumference of the tire is therefore 3π by C=d(π). After 200 revolutions, the tire and car have gone 3π x 200 = 600π feet.
A circle has the equation below. What is the circumference of the circle?
(x – 2)2 + (y + 3)2 = 9
A circle has the equation below. What is the circumference of the circle?
(x – 2)2 + (y + 3)2 = 9
Tap to see back →
The radius is 3. Yielding a circumference of  .
.
The radius is 3. Yielding a circumference of 
The diameter of a circle is defined by the two points (2,5) and (4,6). What is the circumference of this circle?
The diameter of a circle is defined by the two points (2,5) and (4,6). What is the circumference of this circle?
Tap to see back →
We first must calculate the distance between these two points. Recall that the distance formula is:√((x2 - x1)2 + (y2 - y1)2)
For us, it is therefore: √((4 - 2)2 + (6 - 5)2) = √((2)2 + (1)2) = √(4 + 1) = √5
If d = √5, the circumference of our circle is πd, or π√5.
We first must calculate the distance between these two points. Recall that the distance formula is:√((x2 - x1)2 + (y2 - y1)2)
For us, it is therefore: √((4 - 2)2 + (6 - 5)2) = √((2)2 + (1)2) = √(4 + 1) = √5
If d = √5, the circumference of our circle is πd, or π√5.

In the circle above, the length of arc BC is 100 degrees, and the segment AC is a diameter. What is the measure of angle ADB in degrees?
In the circle above, the length of arc BC is 100 degrees, and the segment AC is a diameter. What is the measure of angle ADB in degrees?
Tap to see back →
Since we know that segment AC is a diameter, this means that the length of the arc ABC must be 180 degrees. This means that the length of the arc AB must be 80 degrees.
Since angle ADB is an inscribed angle, its measure is equal to half of the measure of the angle of the arc that it intercepts. This means that the measure of the angle is half of 80 degrees, or 40 degrees.
Since we know that segment AC is a diameter, this means that the length of the arc ABC must be 180 degrees. This means that the length of the arc AB must be 80 degrees.
Since angle ADB is an inscribed angle, its measure is equal to half of the measure of the angle of the arc that it intercepts. This means that the measure of the angle is half of 80 degrees, or 40 degrees.
The length of an arc,  , of a circle is
, of a circle is  and the radius,
and the radius,  , of the circle is
, of the circle is  . What is the measure in degrees of the central angle,
. What is the measure in degrees of the central angle,  , formed by the arc
, formed by the arc  ?
?
The length of an arc, 





Tap to see back →
The circumference of the circle is  .
.

The length of the arc S is  .
.
A ratio can be established:


Solving for _ _yields 90o.
_yields 90o.
Note: This makes sense. Since the arc S was one-fourth the circumference of the circle, the central angle formed by arc S should be one-fourth the total degrees of a circle.
The circumference of the circle is 
The length of the arc S is 
A ratio can be established:
Solving for _
Note: This makes sense. Since the arc S was one-fourth the circumference of the circle, the central angle formed by arc S should be one-fourth the total degrees of a circle.

Note: Figure NOT drawn to scale.
The area of the gray sector in the above circle is  . The area of the white sector is
. The area of the white sector is  . Evaluate
. Evaluate  .
.

Note: Figure NOT drawn to scale.
The area of the gray sector in the above circle is 


Tap to see back →
The total area of the circle is the sum of the areas of the white and gray sectors, or

The gray sector takes up

of the circle, so the degree measure of the gray sector  is equal to
is equal to

The total area of the circle is the sum of the areas of the white and gray sectors, or
The gray sector takes up
of the circle, so the degree measure of the gray sector 
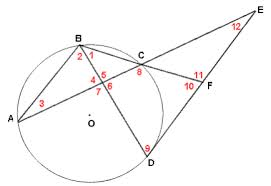
In the figure above that includes Circle O, the measure of angle BAC is equal to 35 degrees, the measure of angle FBD is equal to 40 degrees, and the measure of arc AD is twice the measure of arc AB. Which of the following is the measure of angle CEF? The figure is not necessarily drawn to scale, and the red numbers are used to mark the angles, not represent angle measures.

In the figure above that includes Circle O, the measure of angle BAC is equal to 35 degrees, the measure of angle FBD is equal to 40 degrees, and the measure of arc AD is twice the measure of arc AB. Which of the following is the measure of angle CEF? The figure is not necessarily drawn to scale, and the red numbers are used to mark the angles, not represent angle measures.
Tap to see back →
The measure of angle CEF is going to be equal to half of the difference between the measures two arcs that it intercepts, namely arcs AD and CD.

Thus, we need to find the measure of arcs AD and CD. Let's look at the information given and determine how it can help us figure out the measures of arcs AD and CD.
Angle BAC is an inscribed angle, which means that its meausre is one-half of the measure of the arc that it incercepts, which is arc BC.


Thus, since angle BAC is 35 degrees, the measure of arc BC must be 70 degrees.
We can use a similar strategy to find the measure of arc CD, which is the arc intercepted by the inscribed angle FBD.

Because angle FBD has a measure of 40 degrees, the measure of arc CD must be 80 degrees.
We have the measures of arcs BC and CD. But we still need the measure of arc AD. We can use the last piece of information given, along with our knowledge about the sum of the arcs of a circle, to determine the measure of arc AD.
We are told that the measure of arc AD is twice the measure of arc AB. We also know that the sum of the measures of arcs AD, AB, CD, and BC must be 360 degrees, because there are 360 degrees in a full circle.



Because AD = 2AB, we can substitute 2AB for AD.



This means the measure of arc AB is 70 degrees, and the measure of arc AD is 2(70) = 140 degrees.
Now, we have all the information we need to find the measure of angle CEF, which is equal to half the difference between the measure of arcs AD and CD.



The measure of angle CEF is going to be equal to half of the difference between the measures two arcs that it intercepts, namely arcs AD and CD.
Thus, we need to find the measure of arcs AD and CD. Let's look at the information given and determine how it can help us figure out the measures of arcs AD and CD.
Angle BAC is an inscribed angle, which means that its meausre is one-half of the measure of the arc that it incercepts, which is arc BC.
Thus, since angle BAC is 35 degrees, the measure of arc BC must be 70 degrees.
We can use a similar strategy to find the measure of arc CD, which is the arc intercepted by the inscribed angle FBD.
Because angle FBD has a measure of 40 degrees, the measure of arc CD must be 80 degrees.
We have the measures of arcs BC and CD. But we still need the measure of arc AD. We can use the last piece of information given, along with our knowledge about the sum of the arcs of a circle, to determine the measure of arc AD.
We are told that the measure of arc AD is twice the measure of arc AB. We also know that the sum of the measures of arcs AD, AB, CD, and BC must be 360 degrees, because there are 360 degrees in a full circle.
Because AD = 2AB, we can substitute 2AB for AD.
This means the measure of arc AB is 70 degrees, and the measure of arc AD is 2(70) = 140 degrees.
Now, we have all the information we need to find the measure of angle CEF, which is equal to half the difference between the measure of arcs AD and CD.
A pie has a diameter of 12". A piece is cut out, having a surface area of 4.5π. What is the angle of the cut?
A pie has a diameter of 12". A piece is cut out, having a surface area of 4.5π. What is the angle of the cut?
Tap to see back →
This is simply a matter of percentages. We first have to figure out what percentage of the surface area is represented by 4.5π. To do that, we must calculate the total surface area. If the diameter is 12, the radius is 6. Don't be tricked by this!
A = π * 6 * 6 = 36π
Now, 4.5π is 4.5π/36π percentage or 0.125 (= 12.5%)
To figure out the angle, we must take that percentage of 360°:
0.125 * 360 = 45°
This is simply a matter of percentages. We first have to figure out what percentage of the surface area is represented by 4.5π. To do that, we must calculate the total surface area. If the diameter is 12, the radius is 6. Don't be tricked by this!
A = π * 6 * 6 = 36π
Now, 4.5π is 4.5π/36π percentage or 0.125 (= 12.5%)
To figure out the angle, we must take that percentage of 360°:
0.125 * 360 = 45°
Eric is riding a Ferris wheel. The Ferris wheel has 18 compartments, numbered in order clockwise. If compartment 1 is at 0 degrees and Eric enters compartment 13, what angle is he at?
Eric is riding a Ferris wheel. The Ferris wheel has 18 compartments, numbered in order clockwise. If compartment 1 is at 0 degrees and Eric enters compartment 13, what angle is he at?
Tap to see back →
12 compartments further means 240 more degrees. 240 is the answer.
360/12 = 240 degrees
12 compartments further means 240 more degrees. 240 is the answer.
360/12 = 240 degrees

Note: Figure NOT drawn to scale.
In the above circle,  . Give the ratio of the area of the white sector to that of the gray sector.
. Give the ratio of the area of the white sector to that of the gray sector.

Note: Figure NOT drawn to scale.
In the above circle, 
Tap to see back →
A  sector is
sector is  of the circle. The white sector is therefore
of the circle. The white sector is therefore  of the circle, and the ratio of their areas is
of the circle, and the ratio of their areas is
 ,
,
which simplifies to
 .
.
A 



which simplifies to


Note: Figure NOT drawn to scale.
Refer to the above figure. The ratio of the area of the white sector to that of the gray sector is 5 to 1. Evaluate  .
.

Note: Figure NOT drawn to scale.
Refer to the above figure. The ratio of the area of the white sector to that of the gray sector is 5 to 1. Evaluate 
Tap to see back →
The ratio of the areas is 5 to 1, so the white sector is one sixth of the circle. This means that the central angle of the white sector is one sixth of  .
.
The ratio of the areas is 5 to 1, so the white sector is one sixth of the circle. This means that the central angle of the white sector is one sixth of 
Two pizzas are made to the same dimensions. The only difference is that Pizza 1 is cut into pieces at 30° angles and Pizza 2 is cut at 45° angles. They are sold by the piece, the first for $1.95 per slice and the second for $2.25 per slice. What is the difference in total revenue between Pizza 2 and Pizza 1?
Two pizzas are made to the same dimensions. The only difference is that Pizza 1 is cut into pieces at 30° angles and Pizza 2 is cut at 45° angles. They are sold by the piece, the first for $1.95 per slice and the second for $2.25 per slice. What is the difference in total revenue between Pizza 2 and Pizza 1?
Tap to see back →
First, let's calculate how many slices there are per pizza. This is done by dividing 360° by the respective slice degrees:
Pizza 1: 360/30 = 12 slices
Pizza 2: 360/45 = 8 slices
Now, the total amount made per pizza is calculated by multiplying the number of slices by the respective cost per slice:
Pizza 1: 12 * 1.95 = $23.40
Pizza 2: 8 * 2.25 = $18.00
The difference between Pizza 2 and Pizza 1 is thus represented by: 18 – 23.40 = –$5.40
First, let's calculate how many slices there are per pizza. This is done by dividing 360° by the respective slice degrees:
Pizza 1: 360/30 = 12 slices
Pizza 2: 360/45 = 8 slices
Now, the total amount made per pizza is calculated by multiplying the number of slices by the respective cost per slice:
Pizza 1: 12 * 1.95 = $23.40
Pizza 2: 8 * 2.25 = $18.00
The difference between Pizza 2 and Pizza 1 is thus represented by: 18 – 23.40 = –$5.40

Note: Figure NOT drawn to scale.
In the above circle, the length of arc  is
is  , and the length of arc
, and the length of arc  is
is  . Evaluate
. Evaluate  .
.

Note: Figure NOT drawn to scale.
In the above circle, the length of arc 




Tap to see back →
The circumference of the circle is the sum of the lengths of the arcs  and
and  , which is
, which is

 is therefore
is therefore

of the circle, and its degree measure  is
is

The circumference of the circle is the sum of the lengths of the arcs 


of the circle, and its degree measure 
What is the angle of a sector of area 
 on a circle having a radius of
on a circle having a radius of  ?
?
What is the angle of a sector of area 


Tap to see back →
To begin, you should compute the complete area of the circle:

For your data, this is:

Now, to find the angle measure of a sector, you find what portion of the circle the sector is. Here, it is:

Now, multiply this by the total  degrees in a circle:
degrees in a circle:

Rounded, this is  .
.
To begin, you should compute the complete area of the circle:
For your data, this is:
Now, to find the angle measure of a sector, you find what portion of the circle the sector is. Here, it is:
Now, multiply this by the total 
Rounded, this is 
What is the angle of a sector that has an arc length of 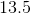
 on a circle of diameter
on a circle of diameter 
 ?
?
What is the angle of a sector that has an arc length of 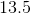



Tap to see back →
The first thing to do for this problem is to compute the total circumference of the circle. Notice that you were given the diameter. The proper equation is therefore:

For your data, this means,

Now, to compute the angle, note that you have a percentage of the total circumference, based upon your arc length:

Rounded to the nearest hundredth, this is  .
.
The first thing to do for this problem is to compute the total circumference of the circle. Notice that you were given the diameter. The proper equation is therefore:
For your data, this means,
Now, to compute the angle, note that you have a percentage of the total circumference, based upon your arc length:
Rounded to the nearest hundredth, this is 

The radius of the circle above is  and
and  . What is the area of the shaded section of the circle?
. What is the area of the shaded section of the circle?

The radius of the circle above is 

Tap to see back →
Area of Circle = πr2 = π42 = 16π
Total degrees in a circle = 360
Therefore 45 degree slice = 45/360 fraction of circle = 1/8
Shaded Area = 1/8 * Total Area = 1/8 * 16π = 2π
Area of Circle = πr2 = π42 = 16π
Total degrees in a circle = 360
Therefore 45 degree slice = 45/360 fraction of circle = 1/8
Shaded Area = 1/8 * Total Area = 1/8 * 16π = 2π
What is the measure, in degrees, of the acute angle formed by the hands of a 12-hour clock that reads exactly 3:10?
What is the measure, in degrees, of the acute angle formed by the hands of a 12-hour clock that reads exactly 3:10?
Tap to see back →
The entire clock measures 360°. As the clock is divided into 12 sections, the distance between each number is equivalent to 30° (360/12). The distance between the 2 and the 3 on the clock is 30°. One has to account, however, for the 10 minutes that have passed. 10 minutes is 1/6 of an hour so the hour hand has also moved 1/6 of the distance between the 3 and the 4, which adds 5° (1/6 of 30°). The total measure of the angle, therefore, is 35°.
The entire clock measures 360°. As the clock is divided into 12 sections, the distance between each number is equivalent to 30° (360/12). The distance between the 2 and the 3 on the clock is 30°. One has to account, however, for the 10 minutes that have passed. 10 minutes is 1/6 of an hour so the hour hand has also moved 1/6 of the distance between the 3 and the 4, which adds 5° (1/6 of 30°). The total measure of the angle, therefore, is 35°.
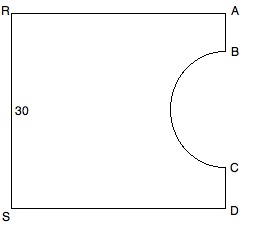
 is a square.
is a square.

The arc from  to
to  is a semicircle with a center at the midpoint of
is a semicircle with a center at the midpoint of  .
.
All units are in feet.
The diagram shows a plot of land.
The cost of summer upkeep is $2.50 per square foot.
In dollars, what is the total upkeep cost for the summer?


The arc from 


All units are in feet.
The diagram shows a plot of land.
The cost of summer upkeep is $2.50 per square foot.
In dollars, what is the total upkeep cost for the summer?
Tap to see back →
To solve this, we must begin by finding the area of the diagram, which is the area of the square less the area of the semicircle.
The area of the square is straightforward:
30 * 30 = 900 square feet
Because each side is 30 feet long, AB + BC + CD = 30.
We can substitute BC for AB and CD since all three lengths are the same:
BC + BC + BC = 30
3BC = 30
BC = 10
Therefore the diameter of the semicircle is 10 feet, so the radius is 5 feet.
The area of the semi-circle is half the area of a circle with radius 5. The area of the full circle is 52π = 25π, so the area of the semi-circle is half of that, or 12.5π.
The total area of the plot is the square less the semicircle: 900 - 12.5π square feet
The cost of upkeep is therefore 2.5 * (900 – 12.5π) = $(2250 – 31.25π).
To solve this, we must begin by finding the area of the diagram, which is the area of the square less the area of the semicircle.
The area of the square is straightforward:
30 * 30 = 900 square feet
Because each side is 30 feet long, AB + BC + CD = 30.
We can substitute BC for AB and CD since all three lengths are the same:
BC + BC + BC = 30
3BC = 30
BC = 10
Therefore the diameter of the semicircle is 10 feet, so the radius is 5 feet.
The area of the semi-circle is half the area of a circle with radius 5. The area of the full circle is 52π = 25π, so the area of the semi-circle is half of that, or 12.5π.
The total area of the plot is the square less the semicircle: 900 - 12.5π square feet
The cost of upkeep is therefore 2.5 * (900 – 12.5π) = $(2250 – 31.25π).
A circular, 8-slice pizza is placed in a square box that has dimensions four inches larger than the diameter of the pizza. If the box covers a surface area of 256 in2, what is the surface area of one piece of pizza?
A circular, 8-slice pizza is placed in a square box that has dimensions four inches larger than the diameter of the pizza. If the box covers a surface area of 256 in2, what is the surface area of one piece of pizza?
Tap to see back →
The first thing to do is calculate the dimensions of the pizza box. Based on our data, we know 256 = s2. Solving for s (by taking the square root of both sides), we get 16 = s (or s = 16).
Now, we know that the diameter of the pizza is four inches less than 16 inches. That is, it is 12 inches. Be careful! The area of the circle is given in terms of radius, which is half the diameter, or 6 inches. Therefore, the area of the pizza is π * 62 = 36π in2. If the pizza is 8-slices, one slice is equal to 1/8 of the total pizza or (36π)/8 = 4.5π in2.
The first thing to do is calculate the dimensions of the pizza box. Based on our data, we know 256 = s2. Solving for s (by taking the square root of both sides), we get 16 = s (or s = 16).
Now, we know that the diameter of the pizza is four inches less than 16 inches. That is, it is 12 inches. Be careful! The area of the circle is given in terms of radius, which is half the diameter, or 6 inches. Therefore, the area of the pizza is π * 62 = 36π in2. If the pizza is 8-slices, one slice is equal to 1/8 of the total pizza or (36π)/8 = 4.5π in2.