Fractions and Percentage - PSAT Math
Card 0 of 119
Write as a fraction: 22%
Write as a fraction: 22%
Tap to see back →
22% = 22/100
Divide everything by 2:
22/100 = 11/50
11 is a prime number, so this is as reduced as this fraction can get.
22% = 22/100
Divide everything by 2:
22/100 = 11/50
11 is a prime number, so this is as reduced as this fraction can get.
25% of 64 is equal to 5% of what number?
25% of 64 is equal to 5% of what number?
Tap to see back →
25% of 64 is 16 (you can find this with a calculator by 0.25 * 64). Divide 16 by 0.05 (or 1/20) to get the value of the number 16 is 5% of. (Or mental math of 16 * 20)
25% of 64 is 16 (you can find this with a calculator by 0.25 * 64). Divide 16 by 0.05 (or 1/20) to get the value of the number 16 is 5% of. (Or mental math of 16 * 20)
Find the simplified fraction for 
Find the simplified fraction for
Tap to see back →
For any percent  we can write it as a fraction in the form
we can write it as a fraction in the form 
So we can write  as
as 
Then we simplify

So our simplified answer is 
For any percent 
So we can write 
Then we simplify
So our simplified answer is
You have 2 fair dice that each have 6 faces. On one roll, what's the probability that both dice land on an even number?
You have 2 fair dice that each have 6 faces. On one roll, what's the probability that both dice land on an even number?
Tap to see back →
In order to find the probability of rolling two even numbers on 2 dice we need to find the probability of each dice having an even number on the roll and then multiply them together.
The probability of rolling an even number is

because 2, 4, and 6 are even numbers which goes in the numerator and there are 6 total numbers which goes in the denominator. After this we reduce the fraction and get one half. Then we need to muliply this by probability of the second dice having an even number.

In order to find the probability of rolling two even numbers on 2 dice we need to find the probability of each dice having an even number on the roll and then multiply them together.
The probability of rolling an even number is
because 2, 4, and 6 are even numbers which goes in the numerator and there are 6 total numbers which goes in the denominator. After this we reduce the fraction and get one half. Then we need to muliply this by probability of the second dice having an even number.
What is 15% of a $16.73 bill?
What is 15% of a $16.73 bill?
Tap to see back →
We can re write 15% as a fraction and then use proportions to solve.

From here we cross multiply and divide to solve for  .
.

We can re write 15% as a fraction and then use proportions to solve.
From here we cross multiply and divide to solve for 
If a test has a total of  questions and
questions and  of the questions are multiple choice, how many questions are multiple choice?
of the questions are multiple choice, how many questions are multiple choice?
If a test has a total of 

Tap to see back →
To solve this problem we set up a ratio. We want to find  of
of  . Therefore, we set up the following ratio:
. Therefore, we set up the following ratio:

In the case  represents the number of questions that are multiple choice. From here we cross multiply and divide.
represents the number of questions that are multiple choice. From here we cross multiply and divide.

To solve this problem we set up a ratio. We want to find 

In the case 
If there are 3 boys in a class and 7 girls. What percent of the class is made up of boys?
If there are 3 boys in a class and 7 girls. What percent of the class is made up of boys?
Tap to see back →
To solve this problem we set up a ratio of part of total. The part is the number of boys in the class and the total is the number of boys and girls in the class.

now to find the percent we can multiply this fraction by 10/10

From here we can see that it is 30%
To solve this problem we set up a ratio of part of total. The part is the number of boys in the class and the total is the number of boys and girls in the class.
now to find the percent we can multiply this fraction by 10/10
From here we can see that it is 30%
Marker Colors Students Blue 13 Pink 10 Orange 5 Brown 5 Green 7
The above chart shows the number of students in a class who chose each of the five marker colors available.
What percentage of the class chose a green marker?
| Marker Colors | Students |
|---|---|
| Blue | 13 |
| Pink | 10 |
| Orange | 5 |
| Brown | 5 |
| Green | 7 |
The above chart shows the number of students in a class who chose each of the five marker colors available.
What percentage of the class chose a green marker?
Tap to see back →
To figure out what percentage of the class chose green markers, you must first figure out what fraction of the class chose green markers. Then, you must convert that fraction into a percentage.
Figure out the fraction:
7 students chose green markers
40 students total
Fraction of students who chose green: 
To convert this fraction to a percentage, you must multiply the fraction times 100, then divide the numerator by the denominator. You multiply the fraction times 100 because in order to figure out the percent, you must figure out what the fraction means "for (per) every hundred (cent)".

Multiply times 100


Therefore, the answer is  .
.
To figure out what percentage of the class chose green markers, you must first figure out what fraction of the class chose green markers. Then, you must convert that fraction into a percentage.
Figure out the fraction:
7 students chose green markers
40 students total
Fraction of students who chose green:
To convert this fraction to a percentage, you must multiply the fraction times 100, then divide the numerator by the denominator. You multiply the fraction times 100 because in order to figure out the percent, you must figure out what the fraction means "for (per) every hundred (cent)".
Multiply times 100
Therefore, the answer is 
Write 7.5% as a fraction.
Write 7.5% as a fraction.
Tap to see back →
First convert the percentage to a decimal:
7.5% = .075
Then turn this into a fraction:
.075 = 75/1000
Simplify by dividing the numerator and denominator by 25:
75/1000 = 3/40
First convert the percentage to a decimal:
7.5% = .075
Then turn this into a fraction:
.075 = 75/1000
Simplify by dividing the numerator and denominator by 25:
75/1000 = 3/40
When y is decreased by ten percent, the result is equal to fifteen percent of x. Assuming both x and y are nonzero, what is the ratio of x to y?
When y is decreased by ten percent, the result is equal to fifteen percent of x. Assuming both x and y are nonzero, what is the ratio of x to y?
Tap to see back →
The problem states that decreasing y by ten percent gives us the same thing as taking fifteen percent of x. We need to find an expression for decreasing y by ten percent, and an expression for fifteen percent of x, and then set these two things equal.
If we were to decrease y by ten percent, we would be left with ninety percent of y (because the percentages must add to one hundred percent). We could write ninety percent of y as 0.90_y_ = (90/100)y = (9/10)y. Remember, when converting from a percent to a decimal, we need to move the decimal two places to the left.
Similarly, we can write 15% of x as 0.15_x_ = (15/100)x = (3/20)x.
Now, we set these two expressions equal to one another.
(9/10)y = (3/20)x
Multiply both sides by 20 to eliminate fractions.
18_y_ = 3_x_
The question asks us to find the ratio of x to y, which is equal to x/y. Thus, we must rearrange the equation above until we have x/y by itself on one side.
18_y_ = 3_x_
Divide both sides by 3.
6_y_ = x
Divide both sides by y.
6 = x/y
Thus, the ratio of x to y is 6.
The answer is 6.
The problem states that decreasing y by ten percent gives us the same thing as taking fifteen percent of x. We need to find an expression for decreasing y by ten percent, and an expression for fifteen percent of x, and then set these two things equal.
If we were to decrease y by ten percent, we would be left with ninety percent of y (because the percentages must add to one hundred percent). We could write ninety percent of y as 0.90_y_ = (90/100)y = (9/10)y. Remember, when converting from a percent to a decimal, we need to move the decimal two places to the left.
Similarly, we can write 15% of x as 0.15_x_ = (15/100)x = (3/20)x.
Now, we set these two expressions equal to one another.
(9/10)y = (3/20)x
Multiply both sides by 20 to eliminate fractions.
18_y_ = 3_x_
The question asks us to find the ratio of x to y, which is equal to x/y. Thus, we must rearrange the equation above until we have x/y by itself on one side.
18_y_ = 3_x_
Divide both sides by 3.
6_y_ = x
Divide both sides by y.
6 = x/y
Thus, the ratio of x to y is 6.
The answer is 6.
Convert 62% into simplified fraction form.
Convert 62% into simplified fraction form.
Tap to see back →
To convert a percent into a fraction, simply divide by 100 and reduce. In our case, 62 and 100 have the common factor of 2, so solving and simplification are as follows:

To convert a percent into a fraction, simply divide by 100 and reduce. In our case, 62 and 100 have the common factor of 2, so solving and simplification are as follows:
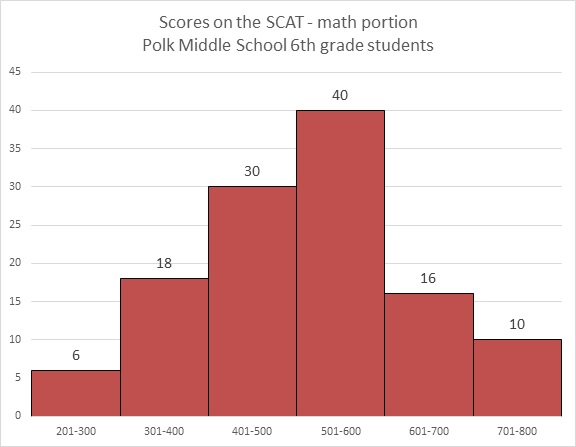
Refer to the above bar graph.
What percent of the students achieved a score 500 or below?

Refer to the above bar graph.
What percent of the students achieved a score 500 or below?
Tap to see back →
6 students achieved a score of 201-300; 18 achieved a score of 301-400; 30 achieved a score of 401-500. Add these:

The number of students who took the test is the sum of the students who finished in the six ranges:

The question is now to find out what percent 54 is of 120, which can be calculated as follows:

6 students achieved a score of 201-300; 18 achieved a score of 301-400; 30 achieved a score of 401-500. Add these:
The number of students who took the test is the sum of the students who finished in the six ranges:
The question is now to find out what percent 54 is of 120, which can be calculated as follows:
Three hens each lay 20 eggs for a farmer. Two-fifths of the first hen's eggs are brown. One-fourth of the second hen's eggs are brown. Seven-tenths of the third hen's eggs are white. What percentage of all the eggs are brown?
Three hens each lay 20 eggs for a farmer. Two-fifths of the first hen's eggs are brown. One-fourth of the second hen's eggs are brown. Seven-tenths of the third hen's eggs are white. What percentage of all the eggs are brown?
Tap to see back →
The first hen lays 8 brown eggs: 2/5 * 20 = 8
The second lays 5 brown eggs: 1/4 * 20 = 5
The third lays 6 brown eggs: 3/10 * 20 = 6
Add up the brown eggs and divide by 60, the total number of eggs:
19/60 = 0.31666667 = 31.67%, or 32%.
The first hen lays 8 brown eggs: 2/5 * 20 = 8
The second lays 5 brown eggs: 1/4 * 20 = 5
The third lays 6 brown eggs: 3/10 * 20 = 6
Add up the brown eggs and divide by 60, the total number of eggs:
19/60 = 0.31666667 = 31.67%, or 32%.
What is  as a percentage?
as a percentage?
What is 
Tap to see back →
Convert the improper fraction  to the mixed numeral
to the mixed numeral  or as the decimal
or as the decimal  .
.  as a percentage is
as a percentage is 
Convert the improper fraction 



A family with 6 children, aged 4, 4, 5, 7, 12, and 13 are moving to a new home. They all want the same bedroom, so the parents have a lottery. Each child places their name in once for every year of age (the four year olds each put their name in 4 times, the seven year old puts his name in 7 times, etc.) What is the probability of the chosen child being 4 years old?
A family with 6 children, aged 4, 4, 5, 7, 12, and 13 are moving to a new home. They all want the same bedroom, so the parents have a lottery. Each child places their name in once for every year of age (the four year olds each put their name in 4 times, the seven year old puts his name in 7 times, etc.) What is the probability of the chosen child being 4 years old?
Tap to see back →
First, we will determine the total number of ballots:
4+4+5+7+12+13=45hspace{1 mm}ballots
Since there are two four year olds, and this question is asking the probability of the chosen child being four, the probability is:
$\frac{4+4}{45}$=\frac{8}{45}$=0.1$\overline{7}$=17.$\overline{7}$%
First, we will determine the total number of ballots:
4+4+5+7+12+13=45hspace{1 mm}ballots
Since there are two four year olds, and this question is asking the probability of the chosen child being four, the probability is:
$\frac{4+4}{45}$=\frac{8}{45}$=0.1$\overline{7}$=17.$\overline{7}$%
There is a sale in a store and every item is discounted 23%. If a shirt is normally $18.59, what is the price of it after the discount?
There is a sale in a store and every item is discounted 23%. If a shirt is normally $18.59, what is the price of it after the discount?
Tap to see back →
We can right 23% as a fraction and set that equal to  over the original price.
over the original price.

From here we cross multiply and divide.

We round this number to $4.28. This is the amount of discoount we need to apply to the original price. To do this we subtract 4.28 from 18.59.

We can right 23% as a fraction and set that equal to 
From here we cross multiply and divide.
We round this number to $4.28. This is the amount of discoount we need to apply to the original price. To do this we subtract 4.28 from 18.59.
Louisa and Caroline are trying to save up to start a small business together. Louisa has saved  of their goal money, and Carolina has saved
of their goal money, and Carolina has saved  of their goal money. About how much of their goal money have they saved up together?
of their goal money. About how much of their goal money have they saved up together?
Louisa and Caroline are trying to save up to start a small business together. Louisa has saved 

Tap to see back →
The goal of this problem is to solve for how much Louisa and Caroline have saved, together, towards their goal money for starting a small business. In order to do that, you must add what Louisa has saved to what Caroline has saved, then convert the fraction into a percentage.
Add Louisa and Caroline:

Find the lowest common multiple for the denominator:

Add:

Simplify:

To convert a fraction into a percentage, simply multiply the numerator by 100 and divide by the denominator. There are other methods, but this is the easiest.

Equals


78% is your answer.
The goal of this problem is to solve for how much Louisa and Caroline have saved, together, towards their goal money for starting a small business. In order to do that, you must add what Louisa has saved to what Caroline has saved, then convert the fraction into a percentage.
Add Louisa and Caroline:
Find the lowest common multiple for the denominator:
Add:
Simplify:
To convert a fraction into a percentage, simply multiply the numerator by 100 and divide by the denominator. There are other methods, but this is the easiest.
Equals
78% is your answer.
Find the simplified fraction for 
Find the simplified fraction for
Tap to see back →
For any percent  we can write it as a fraction in the form
we can write it as a fraction in the form 
So we can write  as
as 
Then we simplify

So our simplified answer is 
For any percent 
So we can write 
Then we simplify
So our simplified answer is
You have 2 fair dice that each have 6 faces. On one roll, what's the probability that both dice land on an even number?
You have 2 fair dice that each have 6 faces. On one roll, what's the probability that both dice land on an even number?
Tap to see back →
In order to find the probability of rolling two even numbers on 2 dice we need to find the probability of each dice having an even number on the roll and then multiply them together.
The probability of rolling an even number is

because 2, 4, and 6 are even numbers which goes in the numerator and there are 6 total numbers which goes in the denominator. After this we reduce the fraction and get one half. Then we need to muliply this by probability of the second dice having an even number.

In order to find the probability of rolling two even numbers on 2 dice we need to find the probability of each dice having an even number on the roll and then multiply them together.
The probability of rolling an even number is
because 2, 4, and 6 are even numbers which goes in the numerator and there are 6 total numbers which goes in the denominator. After this we reduce the fraction and get one half. Then we need to muliply this by probability of the second dice having an even number.
What is 15% of a $16.73 bill?
What is 15% of a $16.73 bill?
Tap to see back →
We can re write 15% as a fraction and then use proportions to solve.

From here we cross multiply and divide to solve for  .
.

We can re write 15% as a fraction and then use proportions to solve.
From here we cross multiply and divide to solve for 