Write the Equation of a Polynomial Function Based on Its Graph - Pre-Calculus
Card 0 of 28
Which could be the equation for this graph?

Which could be the equation for this graph?
This graph has zeros at 3, -2, and -4.5. This means that  ,
,  , and
, and  . That last root is easier to work with if we consider it as
. That last root is easier to work with if we consider it as  and simplify it to
and simplify it to  . Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
. Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
Our equation results from multiplying  , which results in
, which results in  .
.
This graph has zeros at 3, -2, and -4.5. This means that 




Our equation results from multiplying 

Compare your answer with the correct one above
Write the quadratic function for the graph:

Write the quadratic function for the graph:

Method 1:
The x-intercepts are  . These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
. These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
For  ,
,  . For
. For  ,
,  . These equations determine the resulting factors and the resulting function;
. These equations determine the resulting factors and the resulting function;  .
.
Multiplying the factors and simplifying,
 .
.
Answer:  .
.
Method 2:
Use the form  , where
, where  is the vertex.
is the vertex.
 is
is  , so
, so  ,
,  .
.
![(x - $[-4])^{2}$ + (-4) = (x + $4)^{2}$ - 4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/478227/gif.latex)
Answer: 



Method 1:
The x-intercepts are 
For 




Multiplying the factors and simplifying,

Answer: 
Method 2:
Use the form 





Answer:
Compare your answer with the correct one above
Write the quadratic function for the graph:

Write the quadratic function for the graph:

Because there are no x-intercepts, use the form  , where vertex
, where vertex  is
is  , so
, so  ,
,  , which gives
, which gives





Because there are no x-intercepts, use the form 




Compare your answer with the correct one above
Write the equation for the polynomial in this graph:
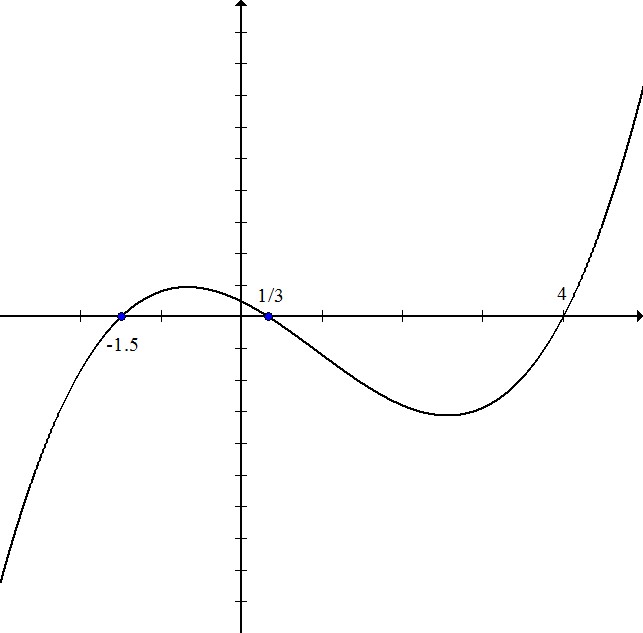
Write the equation for the polynomial in this graph:

The zeros for this polynomial are  .
.
This means that the factors are equal to zero when these values are plugged in for x.
 multiply both sides by 2
multiply both sides by 2
 so one factor is
so one factor is 
 multiply both sides by 3
multiply both sides by 3
 so one factor is
so one factor is 
 so one factor is
so one factor is 
Multiply these three factors:



The zeros for this polynomial are 
This means that the factors are equal to zero when these values are plugged in for x.





Multiply these three factors:
Compare your answer with the correct one above
Write the equation for the polynomial shown in this graph:

Write the equation for the polynomial shown in this graph:

The zeros of this polynomial are  . This means that the factors equal zero when these values are plugged in.
. This means that the factors equal zero when these values are plugged in.
One factor is 
One factor is 
The third factor is equivalent to  . Set equal to 0 and multiply by 2:
. Set equal to 0 and multiply by 2:


Multiply these three factors:


The graph is negative since it goes down then up then down, so we have to switch all of the signs:

The zeros of this polynomial are 
One factor is
One factor is
The third factor is equivalent to 
Multiply these three factors:
The graph is negative since it goes down then up then down, so we have to switch all of the signs:
Compare your answer with the correct one above
Write the equation for the polynomial in this graph:

Write the equation for the polynomial in this graph:

The zeros for this polynomial are  . That means that the factors are equal to zero when these values are plugged in.
. That means that the factors are equal to zero when these values are plugged in.
 or equivalently
or equivalently  multiply both sides by 4
multiply both sides by 4
 the first factor is
the first factor is 
 multiply both sides by 3
multiply both sides by 3
 the second factor is
the second factor is 
 the third factor is
the third factor is 
Multiply the three factors:



The zeros for this polynomial are 






Multiply the three factors:
Compare your answer with the correct one above
Write the equation for the polynomial in the graph:
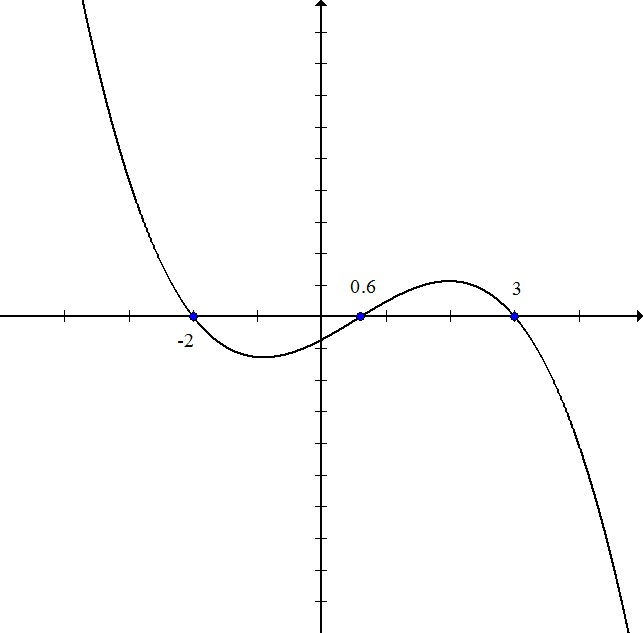
Write the equation for the polynomial in the graph:

The zeros of the polynomial are  . That means that the factors equal zero when these values are plugged in.
. That means that the factors equal zero when these values are plugged in.
The first factor is  or equivalently
or equivalently  multiply both sides by 5:
multiply both sides by 5:

The second and third factors are  and
and 
Multiply:



Because the graph goes down-up-down instead of the standard up-down-up, the graph is negative, so change all of the signs:

The zeros of the polynomial are 
The first factor is 

The second and third factors are 
Multiply:
Because the graph goes down-up-down instead of the standard up-down-up, the graph is negative, so change all of the signs:
Compare your answer with the correct one above
Which could be the equation for this graph?

Which could be the equation for this graph?
This graph has zeros at 3, -2, and -4.5. This means that  ,
,  , and
, and  . That last root is easier to work with if we consider it as
. That last root is easier to work with if we consider it as  and simplify it to
and simplify it to  . Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
. Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
Our equation results from multiplying  , which results in
, which results in  .
.
This graph has zeros at 3, -2, and -4.5. This means that 




Our equation results from multiplying 

Compare your answer with the correct one above
Write the quadratic function for the graph:

Write the quadratic function for the graph:

Method 1:
The x-intercepts are  . These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
. These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
For  ,
,  . For
. For  ,
,  . These equations determine the resulting factors and the resulting function;
. These equations determine the resulting factors and the resulting function;  .
.
Multiplying the factors and simplifying,
 .
.
Answer:  .
.
Method 2:
Use the form  , where
, where  is the vertex.
is the vertex.
 is
is  , so
, so  ,
,  .
.
![(x - $[-4])^{2}$ + (-4) = (x + $4)^{2}$ - 4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/478227/gif.latex)
Answer: 



Method 1:
The x-intercepts are 
For 




Multiplying the factors and simplifying,

Answer: 
Method 2:
Use the form 





Answer:
Compare your answer with the correct one above
Write the quadratic function for the graph:

Write the quadratic function for the graph:

Because there are no x-intercepts, use the form  , where vertex
, where vertex  is
is  , so
, so  ,
,  , which gives
, which gives





Because there are no x-intercepts, use the form 




Compare your answer with the correct one above
Write the equation for the polynomial in this graph:

Write the equation for the polynomial in this graph:

The zeros for this polynomial are  .
.
This means that the factors are equal to zero when these values are plugged in for x.
 multiply both sides by 2
multiply both sides by 2
 so one factor is
so one factor is 
 multiply both sides by 3
multiply both sides by 3
 so one factor is
so one factor is 
 so one factor is
so one factor is 
Multiply these three factors:



The zeros for this polynomial are 
This means that the factors are equal to zero when these values are plugged in for x.





Multiply these three factors:
Compare your answer with the correct one above
Write the equation for the polynomial shown in this graph:

Write the equation for the polynomial shown in this graph:

The zeros of this polynomial are  . This means that the factors equal zero when these values are plugged in.
. This means that the factors equal zero when these values are plugged in.
One factor is 
One factor is 
The third factor is equivalent to  . Set equal to 0 and multiply by 2:
. Set equal to 0 and multiply by 2:


Multiply these three factors:


The graph is negative since it goes down then up then down, so we have to switch all of the signs:

The zeros of this polynomial are 
One factor is
One factor is
The third factor is equivalent to 
Multiply these three factors:
The graph is negative since it goes down then up then down, so we have to switch all of the signs:
Compare your answer with the correct one above
Write the equation for the polynomial in this graph:

Write the equation for the polynomial in this graph:

The zeros for this polynomial are  . That means that the factors are equal to zero when these values are plugged in.
. That means that the factors are equal to zero when these values are plugged in.
 or equivalently
or equivalently  multiply both sides by 4
multiply both sides by 4
 the first factor is
the first factor is 
 multiply both sides by 3
multiply both sides by 3
 the second factor is
the second factor is 
 the third factor is
the third factor is 
Multiply the three factors:



The zeros for this polynomial are 






Multiply the three factors:
Compare your answer with the correct one above
Write the equation for the polynomial in the graph:

Write the equation for the polynomial in the graph:

The zeros of the polynomial are  . That means that the factors equal zero when these values are plugged in.
. That means that the factors equal zero when these values are plugged in.
The first factor is  or equivalently
or equivalently  multiply both sides by 5:
multiply both sides by 5:

The second and third factors are  and
and 
Multiply:



Because the graph goes down-up-down instead of the standard up-down-up, the graph is negative, so change all of the signs:

The zeros of the polynomial are 
The first factor is 

The second and third factors are 
Multiply:
Because the graph goes down-up-down instead of the standard up-down-up, the graph is negative, so change all of the signs:
Compare your answer with the correct one above
Write the quadratic function for the graph:

Write the quadratic function for the graph:

Method 1:
The x-intercepts are  . These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
. These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.
For  ,
,  . For
. For  ,
,  . These equations determine the resulting factors and the resulting function;
. These equations determine the resulting factors and the resulting function;  .
.
Multiplying the factors and simplifying,
 .
.
Answer:  .
.
Method 2:
Use the form  , where
, where  is the vertex.
is the vertex.
 is
is  , so
, so  ,
,  .
.
![(x - $[-4])^{2}$ + (-4) = (x + $4)^{2}$ - 4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/478227/gif.latex)
Answer: 



Method 1:
The x-intercepts are 
For 




Multiplying the factors and simplifying,

Answer: 
Method 2:
Use the form 





Answer:
Compare your answer with the correct one above
Write the quadratic function for the graph:

Write the quadratic function for the graph:

Because there are no x-intercepts, use the form  , where vertex
, where vertex  is
is  , so
, so  ,
,  , which gives
, which gives





Because there are no x-intercepts, use the form 




Compare your answer with the correct one above
Which could be the equation for this graph?

Which could be the equation for this graph?
This graph has zeros at 3, -2, and -4.5. This means that  ,
,  , and
, and  . That last root is easier to work with if we consider it as
. That last root is easier to work with if we consider it as  and simplify it to
and simplify it to  . Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
. Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.
Our equation results from multiplying  , which results in
, which results in  .
.
This graph has zeros at 3, -2, and -4.5. This means that 




Our equation results from multiplying 

Compare your answer with the correct one above
Write the equation for the polynomial in this graph:

Write the equation for the polynomial in this graph:

The zeros for this polynomial are  .
.
This means that the factors are equal to zero when these values are plugged in for x.
 multiply both sides by 2
multiply both sides by 2
 so one factor is
so one factor is 
 multiply both sides by 3
multiply both sides by 3
 so one factor is
so one factor is 
 so one factor is
so one factor is 
Multiply these three factors:



The zeros for this polynomial are 
This means that the factors are equal to zero when these values are plugged in for x.





Multiply these three factors:
Compare your answer with the correct one above
Write the equation for the polynomial shown in this graph:

Write the equation for the polynomial shown in this graph:

The zeros of this polynomial are  . This means that the factors equal zero when these values are plugged in.
. This means that the factors equal zero when these values are plugged in.
One factor is 
One factor is 
The third factor is equivalent to  . Set equal to 0 and multiply by 2:
. Set equal to 0 and multiply by 2:


Multiply these three factors:


The graph is negative since it goes down then up then down, so we have to switch all of the signs:

The zeros of this polynomial are 
One factor is
One factor is
The third factor is equivalent to 
Multiply these three factors:
The graph is negative since it goes down then up then down, so we have to switch all of the signs:
Compare your answer with the correct one above
Write the equation for the polynomial in this graph:

Write the equation for the polynomial in this graph:

The zeros for this polynomial are  . That means that the factors are equal to zero when these values are plugged in.
. That means that the factors are equal to zero when these values are plugged in.
 or equivalently
or equivalently  multiply both sides by 4
multiply both sides by 4
 the first factor is
the first factor is 
 multiply both sides by 3
multiply both sides by 3
 the second factor is
the second factor is 
 the third factor is
the third factor is 
Multiply the three factors:



The zeros for this polynomial are 






Multiply the three factors:
Compare your answer with the correct one above