Graphs of Polynomial Functions - Pre-Calculus

Card 0 of 52

Give the -intercept of the graph of the function

$f(x) = 5 \cdot $4^{x- 3}$- 3$

Round to the nearest tenth, if applicable.

Tap to see back →

The -intercept is , where :

$f(x) = 5 \cdot $4^{x- 3}$- 3$

$5 \cdot $4^{a- 3}$- 3 = 0$

$5 \cdot $4^{a- 3}$- 3 + 3= 0 + 3$

$5 \cdot $4^{a- 3}$= 3$

$5 \cdot $4^{a- 3}$ \div 5= 3 \div 5$

$\ln \left $(4^{a- 3}$ \right )=\ln 0.6$

$(a- 3)\ln 4 =\ln 0.6$

$a- 3=\frac{\ln 0.6}{\ln 4 }$ \approx $\frac{-0.5108}{1.3863}$\approx -0.3685$

$a- 3+3 \approx -0.3685 + 3$

$a \approx 2.63$

The -intercept is .

Which of the following is an accurate graph of $f(x) = -(x + $4)^{2}$$ ?

Tap to see back →

is a parabola, because of the general $f(x) = $x^{2}$$ structure. The parabola opens downward because .

Solving $-(x + $4)^{2}$ = 0$ tells the x-value of the x-axis intercept;

$0 = (x + $4)^{2}$$

$$\sqrt{0}$ = $\sqrt{(x + $4)^{2}$$}$

The resulting x-axis intercept is: .

Setting tells the y-value of the y-axis intercept;

$y = -(0 + $4)^{2}$$

$= $-1(4)^{2}$$

The resulting y-axis intercept is:

Graph the following function and identify the zeros.

Tap to see back →

This question tests one's ability to graph a polynomial function.

For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Use algebraic technique to factor the function.

Separating the function into two parts...

Factoring a negative one from the second set results in...

Factoring out from the first set results in...

The new factored form of the function is,

.

Now, recognize that the first binomial is a perfect square for which the following formula can be used

$(x^2-b^2)=(x-\sqrt{b})(x+\sqrt{b})$

since

$b=1\Rightarrow \sqrt{b}=\pm1$

thus the simplified, factored form is,

.

Step 2: Identify the roots of the function.

To find the roots of a function set its factored form equal to zero and solve for the possible x values.

$\(x-1)(x+1)(x-2)=0 \x-1=0\Rightarrow x=1 \x+1=0\Rightarrow x=-1 \x-2=0\Rightarrow x=2$

Step 3: Create a table of pairs.

$\begin{tabular}{ |c|c|c|c|c|c|c| } \hline x & f(x) & y \ \hline -2& f(-2) & -12 \ -1 & f(-1) & 0 \ 0&f(0)& 2\ 1.5&f(1.5)&-0.625\2&f(2)&0 \ 3&f(3)&8 \\hline \end{tabular}$

The values in the table are found by substituting in the x values into the function as follows.

$\f(-2)=(-2)^3-2(-2)^2-(-2)+2=-8-8+2+2=-16+4=-12 \f(-1)=(-1)^3-2(-1)^2-(-1)+2=-1-2+1+2=0 \f(0)=(0)^3-2(0)^2-(0)+2=0-0-0+2=2 \f(1.5)=(1.5)^3-2(1.5)^2-(1.5)+2=-0.625 \f(2)=(2)^3-2(2)^2-(2)+2=8-8-2+2=0 \f(3)=(3)^3-2(3)^2-(3)+2=27-18-3+2=8$

Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

Graph the function and identify its roots.

Tap to see back →

This question tests one's ability to graph a polynomial function.

For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Use algebraic technique to factor the function.

Recognize that the binomial is a perfect square for which the following formula can be used

since

$\a=4\Rightarrow $\sqrt{a}$=\pm2 \b=36\Rightarrow $\sqrt{b}$=\pm6$

thus the simplified, factored form is,

.

Step 2: Identify the roots of the function.

To find the roots of a function set its factored form equal to zero and solve for the possible x values.

$\2x-6=0 \2x=6 \x=3$ $\2x+6=0 \2x=-6 \x=-3$

Step 3: Create a table of pairs.

$\begin{tabular}{ |c|c|c|c|c|c|c| } \hline x & f(x) & y \ \hline -3& f(-3) & 0 \ -1 & f(-1) & -32 \ 0&f(0)& -36\ 1&f(1)&-32\3&f(3)&0 \\hline \end{tabular}$

The values in the table are found by substituting in the x values into the function as follows.

Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

Which could be the equation for this graph?

Tap to see back →

This graph has zeros at 3, -2, and -4.5. This means that , , and . That last root is easier to work with if we consider it as $x+\frac{9}{2}$=0$ and simplify it to . Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.

Our equation results from multiplying , which results in .

Graph the function and identify its roots.

Tap to see back →

This question tests one's ability to graph a polynomial function.

For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Use algebraic technique to factor the function.

Recognize that the binomial is a perfect square for which the following formula can be used

since

$\a=9\Rightarrow $\sqrt{a}$=\pm3 \b=16\Rightarrow $\sqrt{b}$=\pm4$

thus the simplified, factored form is,

.

Step 2: Identify the roots of the function.

To find the roots of a function set its factored form equal to zero and solve for the possible x values.

$\3x-4=0 \3x=4\x=\frac{4}{3}$$ $\3x+4=0 \3x=-4 \x=-$\frac{4}{3}$$

Step 3: Create a table of pairs.

$\begin{tabular}{ |c|c|c|c|c|c|c| } \hline x & f(x) & y \ \hline -2& f(-2) & 20 \ -4/3 & f(-4/3) & 0 \ 0&f(0)& -16\ 1&f(1)&-7\\hline \end{tabular}$

The values in the table are found by substituting in the x values into the function as follows.

Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

Graph the function and identify the roots.

Tap to see back →

This question tests one's ability to graph a polynomial function.

For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Use algebraic technique to factor the function.

Recognize that the binomial is a perfect square for which the following formula can be used

since

$\a=100\Rightarrow $\sqrt{a}$=\pm10 \b=1\Rightarrow $\sqrt{b}$=\pm1$

thus the simplified, factored form is,

.

Step 2: Identify the roots of the function.

To find the roots of a function set its factored form equal to zero and solve for the possible x values.

$\10x-1=0 \10x=1\ \x=\frac{1}{10}$$ $\10x+1=0 \10x=-1 \x=-$\frac{1}{10}$$

Step 3: Create a table of pairs.

$\begin{tabular}{ |c|c|c|c|c|c|c| } \hline x & f(x) & y \ \hline -1& f(-1) & 99 \ 0 & f(0) & -1 \ 1&f(1)& 99 \\hline \end{tabular}$

The values in the table are found by substituting in the x values into the function as follows.

Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

Write the quadratic function for the graph:

Tap to see back →

Method 1:

The x-intercepts are . These values would be obtained if the original quadratic were factored, or reverse-FOILed and the factors were set equal to zero.

For , . For , . These equations determine the resulting factors and the resulting function; .

Multiplying the factors and simplifying,

$f(x) = x\cdotx + 2\cdotx + 6\cdotx + 6\cdot2 = $x^{2}$ + 8x + 12$ .

Answer: $f(x) = $x^{2}$ + 8x + 12$ .

Method 2:

Use the form $(x - $h)^{2}$ + k$ , where is the vertex.

is , so , .

$(x - $[-4])^{2}$ + (-4) = (x + $4)^{2}$ - 4$

Answer: $f(x) = (x + $4)^{2}$ - 4$

$= $x^{2}$ + 8x +16 - 4$

$= $x^{2}$ + 8x + 12$

Write the quadratic function for the graph:

Tap to see back →

Because there are no x-intercepts, use the form $f(x) = (x - $h)^{2}$ + k$ , where vertex is , so , , which gives

$f(x) = (x - $3)^{2}$ + 3$

$= $x^{2}$ + 2(-3)(x) + $(-3)^{2}$ + 3$

$= $x^{2}$ - 6x + 9 + 3$

$= $x^{2}$ - 6x + 12$

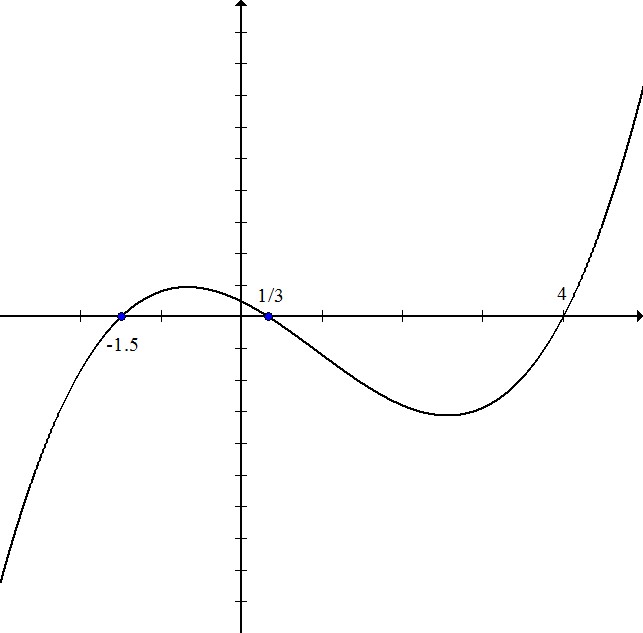
Write the equation for the polynomial in this graph:

Tap to see back →

The zeros for this polynomial are $-1.5, $\frac{1}{3}$, 4$ .

This means that the factors are equal to zero when these values are plugged in for x.

multiply both sides by 2

so one factor is

$x - $\frac{1}{3}$ = 0$ multiply both sides by 3

so one factor is

so one factor is

Multiply these three factors:

Write the equation for the polynomial shown in this graph:

Tap to see back →

The zeros of this polynomial are . This means that the factors equal zero when these values are plugged in.

One factor is

One factor is

The third factor is equivalent to . Set equal to 0 and multiply by 2:

Multiply these three factors:

The graph is negative since it goes down then up then down, so we have to switch all of the signs:

Write the equation for the polynomial in this graph:

Tap to see back →

The zeros for this polynomial are $-1.75, $\frac{1}{3}$, 4$ . That means that the factors are equal to zero when these values are plugged in.

or equivalently $x + $\frac{7}{4}$ = 0$ multiply both sides by 4

the first factor is

$x-$\frac{1}{3}$ = 0$ multiply both sides by 3

the second factor is

the third factor is

Multiply the three factors:

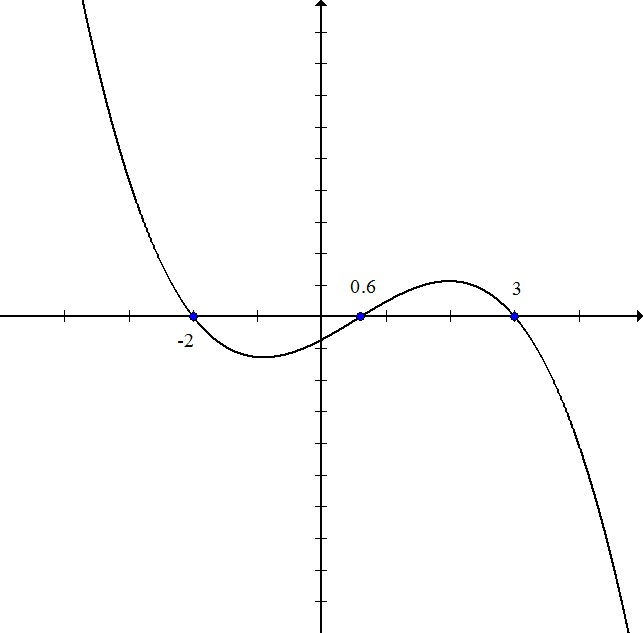
Write the equation for the polynomial in the graph:

Tap to see back →

The zeros of the polynomial are . That means that the factors equal zero when these values are plugged in.

The first factor is or equivalently $x - $\frac{3}{5}$ = 0$ multiply both sides by 5:

The second and third factors are and

Multiply:

Because the graph goes down-up-down instead of the standard up-down-up, the graph is negative, so change all of the signs:

Give the -intercept of the graph of the function

$f(x) = 5 \cdot $4^{x- 3}$- 3$

Round to the nearest tenth, if applicable.

Tap to see back →

The -intercept is , where :

$f(x) = 5 \cdot $4^{x- 3}$- 3$

$5 \cdot $4^{a- 3}$- 3 = 0$

$5 \cdot $4^{a- 3}$- 3 + 3= 0 + 3$

$5 \cdot $4^{a- 3}$= 3$

$5 \cdot $4^{a- 3}$ \div 5= 3 \div 5$

$\ln \left $(4^{a- 3}$ \right )=\ln 0.6$

$(a- 3)\ln 4 =\ln 0.6$

$a- 3=\frac{\ln 0.6}{\ln 4 }$ \approx $\frac{-0.5108}{1.3863}$\approx -0.3685$

$a- 3+3 \approx -0.3685 + 3$

$a \approx 2.63$

The -intercept is .

Which of the following is an accurate graph of $f(x) = -(x + $4)^{2}$$ ?

Tap to see back →

is a parabola, because of the general $f(x) = $x^{2}$$ structure. The parabola opens downward because .

Solving $-(x + $4)^{2}$ = 0$ tells the x-value of the x-axis intercept;

$0 = (x + $4)^{2}$$

$$\sqrt{0}$ = $\sqrt{(x + $4)^{2}$$}$

The resulting x-axis intercept is: .

Setting tells the y-value of the y-axis intercept;

$y = -(0 + $4)^{2}$$

$= $-1(4)^{2}$$

The resulting y-axis intercept is:

Graph the following function and identify the zeros.

Tap to see back →

This question tests one's ability to graph a polynomial function.

For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Use algebraic technique to factor the function.

Separating the function into two parts...

Factoring a negative one from the second set results in...

Factoring out from the first set results in...

The new factored form of the function is,

.

Now, recognize that the first binomial is a perfect square for which the following formula can be used

$(x^2-b^2)=(x-\sqrt{b})(x+\sqrt{b})$

since

$b=1\Rightarrow \sqrt{b}=\pm1$

thus the simplified, factored form is,

.

Step 2: Identify the roots of the function.

To find the roots of a function set its factored form equal to zero and solve for the possible x values.

$\(x-1)(x+1)(x-2)=0 \x-1=0\Rightarrow x=1 \x+1=0\Rightarrow x=-1 \x-2=0\Rightarrow x=2$

Step 3: Create a table of pairs.

$\begin{tabular}{ |c|c|c|c|c|c|c| } \hline x & f(x) & y \ \hline -2& f(-2) & -12 \ -1 & f(-1) & 0 \ 0&f(0)& 2\ 1.5&f(1.5)&-0.625\2&f(2)&0 \ 3&f(3)&8 \\hline \end{tabular}$

The values in the table are found by substituting in the x values into the function as follows.

$\f(-2)=(-2)^3-2(-2)^2-(-2)+2=-8-8+2+2=-16+4=-12 \f(-1)=(-1)^3-2(-1)^2-(-1)+2=-1-2+1+2=0 \f(0)=(0)^3-2(0)^2-(0)+2=0-0-0+2=2 \f(1.5)=(1.5)^3-2(1.5)^2-(1.5)+2=-0.625 \f(2)=(2)^3-2(2)^2-(2)+2=8-8-2+2=0 \f(3)=(3)^3-2(3)^2-(3)+2=27-18-3+2=8$

Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

Graph the function and identify its roots.

Tap to see back →

This question tests one's ability to graph a polynomial function.

For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Use algebraic technique to factor the function.

Recognize that the binomial is a perfect square for which the following formula can be used

since

$\a=4\Rightarrow $\sqrt{a}$=\pm2 \b=36\Rightarrow $\sqrt{b}$=\pm6$

thus the simplified, factored form is,

.

Step 2: Identify the roots of the function.

To find the roots of a function set its factored form equal to zero and solve for the possible x values.

$\2x-6=0 \2x=6 \x=3$ $\2x+6=0 \2x=-6 \x=-3$

Step 3: Create a table of pairs.

$\begin{tabular}{ |c|c|c|c|c|c|c| } \hline x & f(x) & y \ \hline -3& f(-3) & 0 \ -1 & f(-1) & -32 \ 0&f(0)& -36\ 1&f(1)&-32\3&f(3)&0 \\hline \end{tabular}$

The values in the table are found by substituting in the x values into the function as follows.

Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

Which could be the equation for this graph?

Tap to see back →

This graph has zeros at 3, -2, and -4.5. This means that , , and . That last root is easier to work with if we consider it as $x+\frac{9}{2}$=0$ and simplify it to . Also, this is a negative polynomial, because it is decreasing, increasing, decreasing and not the other way around.

Our equation results from multiplying , which results in .

Graph the function and identify its roots.

Tap to see back →

This question tests one's ability to graph a polynomial function.

For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Use algebraic technique to factor the function.

Recognize that the binomial is a perfect square for which the following formula can be used

since

$\a=9\Rightarrow $\sqrt{a}$=\pm3 \b=16\Rightarrow $\sqrt{b}$=\pm4$

thus the simplified, factored form is,

.

Step 2: Identify the roots of the function.

To find the roots of a function set its factored form equal to zero and solve for the possible x values.

$\3x-4=0 \3x=4\x=\frac{4}{3}$$ $\3x+4=0 \3x=-4 \x=-$\frac{4}{3}$$

Step 3: Create a table of pairs.

$\begin{tabular}{ |c|c|c|c|c|c|c| } \hline x & f(x) & y \ \hline -2& f(-2) & 20 \ -4/3 & f(-4/3) & 0 \ 0&f(0)& -16\ 1&f(1)&-7\\hline \end{tabular}$

The values in the table are found by substituting in the x values into the function as follows.

Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.

Graph the function and identify the roots.

Tap to see back →

This question tests one's ability to graph a polynomial function.

For the purpose of Common Core Standards, "graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior" falls within the Cluster C of "Analyze Functions Using Different Representations" concept (CCSS.MATH.CONTENT.HSF-IF.C.7).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Use algebraic technique to factor the function.

Recognize that the binomial is a perfect square for which the following formula can be used

since

$\a=100\Rightarrow $\sqrt{a}$=\pm10 \b=1\Rightarrow $\sqrt{b}$=\pm1$

thus the simplified, factored form is,

.

Step 2: Identify the roots of the function.

To find the roots of a function set its factored form equal to zero and solve for the possible x values.

$\10x-1=0 \10x=1\ \x=\frac{1}{10}$$ $\10x+1=0 \10x=-1 \x=-$\frac{1}{10}$$

Step 3: Create a table of pairs.

$\begin{tabular}{ |c|c|c|c|c|c|c| } \hline x & f(x) & y \ \hline -1& f(-1) & 99 \ 0 & f(0) & -1 \ 1&f(1)& 99 \\hline \end{tabular}$

The values in the table are found by substituting in the x values into the function as follows.

Step 4: Plot the points on a coordinate grid and connect them with a smooth curve.