Graphing Functions - Pre-Calculus
Card 0 of 444
True or false: If you translate a sine curve 90o to the left along the x-axis, you will have a cosine curve.
True or false: If you translate a sine curve 90o to the left along the x-axis, you will have a cosine curve.
Tap to see back →
This is true! Notice the similarity of the shape between the graphs, but that they intercept the x-axis at different spots, and their peaks and valleys are at different spots.
y=sin(x), passes through the point (0,0)

y=cos(x), passes through the point (0,1)

This is true! Notice the similarity of the shape between the graphs, but that they intercept the x-axis at different spots, and their peaks and valleys are at different spots.
y=sin(x), passes through the point (0,0)

y=cos(x), passes through the point (0,1)

What is the amplitude of the following function?

What is the amplitude of the following function?
Tap to see back →
When you think of a trigonometric function of the form y=Asin(Bx+C)+D, the amplitude is represented by A, or the coefficient in front of the sine function. While this number is -24, we always represent amplitude as a positive number, by taking the absolute value of it. Therefore, the amplitude of this function is 24.
When you think of a trigonometric function of the form y=Asin(Bx+C)+D, the amplitude is represented by A, or the coefficient in front of the sine function. While this number is -24, we always represent amplitude as a positive number, by taking the absolute value of it. Therefore, the amplitude of this function is 24.
Select the answer choice that correctly matches each function to its period.
Select the answer choice that correctly matches each function to its period.
Tap to see back →
The following matches the correct period with its corresponding trig function:






In other words, sin x, cos x, sec x, and csc x all repeat themselves every  units. However, tan x and cot x repeat themselves more frequently, every
units. However, tan x and cot x repeat themselves more frequently, every  units.
units.
The following matches the correct period with its corresponding trig function:
In other words, sin x, cos x, sec x, and csc x all repeat themselves every 

What is the period of this sine graph?

What is the period of this sine graph?

Tap to see back →
The graph has 3 waves between 0 and  , meaning that the length of each of the waves is
, meaning that the length of each of the waves is  divided by 3, or
divided by 3, or  .
.
The graph has 3 waves between 0 and 


Write the equation for a cosine graph with a maximum at  and a minimum at
and a minimum at  .
.
Write the equation for a cosine graph with a maximum at 

Tap to see back →
In order to write this equation, it is helpful to sketch a graph:
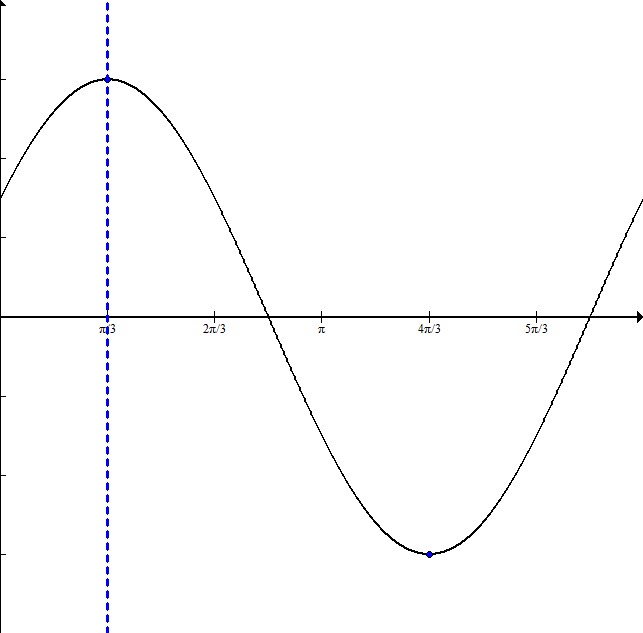
The dotted line is at  , where the maximum occurs and therefore where the graph starts. This means that the graph is shifted to the right
, where the maximum occurs and therefore where the graph starts. This means that the graph is shifted to the right  .
.
The distance from the maximum to the minimum is half the entire wavelength. Here it is  .
.
Since half the wavelength is  , that means the full wavelength is
, that means the full wavelength is  so the frequency is just 1.
so the frequency is just 1.
The amplitude is 3 because the graph goes symmetrically from -3 to 3.
The equation will be in the form  where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.
This equation is
 .
.
In order to write this equation, it is helpful to sketch a graph:

The dotted line is at 

The distance from the maximum to the minimum is half the entire wavelength. Here it is 
Since half the wavelength is 

The amplitude is 3 because the graph goes symmetrically from -3 to 3.
The equation will be in the form 
This equation is

Find the phase shift of  .
.
Find the phase shift of 
Tap to see back →
In the formula,
 .
.
 represents the phase shift.
represents the phase shift.
Plugging in what we know gives us:
 .
.
Simplified, the phase is then  .
.
In the formula,


Plugging in what we know gives us:

Simplified, the phase is then 
Which equation would produce this sine graph?

Which equation would produce this sine graph?
Tap to see back →
The graph has an amplitude of 2 but has been shifted down 1:

In terms of the equation, this puts a 2 in front of sin, and -1 at the end.
This makes it easier to see that the graph starts \[is at 0\] where  .
.
The phase shift is  to the right, or
to the right, or  .
.
The graph has an amplitude of 2 but has been shifted down 1:
In terms of the equation, this puts a 2 in front of sin, and -1 at the end.
This makes it easier to see that the graph starts \[is at 0\] where 
The phase shift is 

Which of the following equations could represent a cosine function with amplitude 3, period  , and a phase shift of
, and a phase shift of  ?
?
Which of the following equations could represent a cosine function with amplitude 3, period 

Tap to see back →
The form of the equation will be 
First, think about all possible values of A that could give you an amplitude of 3. Either A = -3 or A = 3 could each produce amplitude = 3. Be sure to look for answer choices that satisfy either of these.
Secondly, we know that the period is  . Normally we know what B is and need to find the period, but this is the other way around. We can still use the same equation and solve:
. Normally we know what B is and need to find the period, but this is the other way around. We can still use the same equation and solve:
 . You can cross multiply to solve and get B = 4.
. You can cross multiply to solve and get B = 4.
Finally, we need to find a value of C that satisfies
 . Cross multiply to get:
. Cross multiply to get:
 .
.
Next, plug in B= 4 to solve for C:


Putting this all together, the equation could either be:
 or
or 
The form of the equation will be
First, think about all possible values of A that could give you an amplitude of 3. Either A = -3 or A = 3 could each produce amplitude = 3. Be sure to look for answer choices that satisfy either of these.
Secondly, we know that the period is 

Finally, we need to find a value of C that satisfies


Next, plug in B= 4 to solve for C:
Putting this all together, the equation could either be:

State the amplitude, period, phase shift, and vertical shift of the function 
State the amplitude, period, phase shift, and vertical shift of the function
Tap to see back →
A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D,
- amplitude is |A|
- period is 2
 /|B|
/|B|
- phase shift is - C/B
- vertical shift is D
In our equation, A=-7, B=6, C= , and D=-4. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift.
, and D=-4. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift.
To find amplitude, look at the coefficient in front of the sine function. A=-7, so our amplitude is equal to 7.
The period is 2 /B, and in this case B=6. Therefore the period of this function is equal to 2
/B, and in this case B=6. Therefore the period of this function is equal to 2 /6 or
/6 or  /3.
/3.
To find the phase shift, take -C/B, or - /6. Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x.
/6. Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x.
6x+ =0
=0
6x=-
x=- /6
/6
Either way, our phase shift is equal to - /6.
/6.
The vertical shift is equal to D, which is -4.
y=-7\sin(6x+\pi)-4
A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D,
- amplitude is |A|
- period is 2
/|B|
- phase shift is - C/B
- vertical shift is D
In our equation, A=-7, B=6, C=
To find amplitude, look at the coefficient in front of the sine function. A=-7, so our amplitude is equal to 7.
The period is 2


To find the phase shift, take -C/B, or -
6x+
6x=-
x=-
Either way, our phase shift is equal to -
The vertical shift is equal to D, which is -4.
y=-7\sin(6x+\pi)-4
State the amplitude, period, phase shift, and vertical shift of the function 
State the amplitude, period, phase shift, and vertical shift of the function
Tap to see back →
A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D,
- amplitude is |A|
- period is 2
 /|B|
/|B|
- phase shift is - C/B
- vertical shift is D
In our equation, A=-1, B=1, C=- , and D=3. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift.
, and D=3. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift.
To find amplitude, look at the coefficient in front of the sine function. A=-1, so our amplitude is equal to 1.
The period is 2 /B, and in this case B=1. Therefore the period of this function is equal to 2
/B, and in this case B=1. Therefore the period of this function is equal to 2 .
.
To find the phase shift, take -C/B, or  . Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x.
. Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x.
x- =0
=0
x=
Either way, our phase shift is equal to  .
.
The vertical shift is equal to D, which is 3.
A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D,
- amplitude is |A|
- period is 2
/|B|
- phase shift is - C/B
- vertical shift is D
In our equation, A=-1, B=1, C=-
To find amplitude, look at the coefficient in front of the sine function. A=-1, so our amplitude is equal to 1.
The period is 2

To find the phase shift, take -C/B, or 
x-
x=
Either way, our phase shift is equal to 
The vertical shift is equal to D, which is 3.
Which of the following functions is represented by this graph?

Which of the following functions is represented by this graph?

Tap to see back →
This graph is the graph of y = tan x. The domain of this function is all real numbers except  where n is any integer. In other words, there are vertical asymptotes at
where n is any integer. In other words, there are vertical asymptotes at  , and so on. The range of this function is
, and so on. The range of this function is  . The period of this function is
. The period of this function is  .
.
This graph is the graph of y = tan x. The domain of this function is all real numbers except 



State the amplitude, period, phase shift, and vertical shift of the function 
State the amplitude, period, phase shift, and vertical shift of the function
Tap to see back →
A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D,
- amplitude is |A|
- period is 2
 /|B|
/|B|
- phase shift is - C/B
- vertical shift is D
In our equation, A=1, B=2, C=-3, and D=2. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift.
To find amplitude, look at the coefficient in front of the sine function. A=1, so our amplitude is equal to 1.
The period is 2 /B, and in this case B=2. Therefore the period of this function is equal to
/B, and in this case B=2. Therefore the period of this function is equal to  .
.
To find the phase shift, take -C/B, or 3/2. Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x.
2x-3=0
2x=3
x=3/2
Either way, our phase shift is equal to 3/2.
The vertical shift is equal to D, which is 2.
A common way to make sense of all of the transformations that can happen to a trigonometric function is the following. For the equations y = A sin(Bx + C) + D,
- amplitude is |A|
- period is 2
/|B|
- phase shift is - C/B
- vertical shift is D
In our equation, A=1, B=2, C=-3, and D=2. Next, apply the above numbers to find amplitude, period, phase shift, and vertical shift.
To find amplitude, look at the coefficient in front of the sine function. A=1, so our amplitude is equal to 1.
The period is 2

To find the phase shift, take -C/B, or 3/2. Another way to find this same value is to set the inside of the parenthesis equal to 0, then solve for x.
2x-3=0
2x=3
x=3/2
Either way, our phase shift is equal to 3/2.
The vertical shift is equal to D, which is 2.
Information about the Hardy Weinberg equation: http://www.nature.com/scitable/definition/hardy-weinberg-equation-299
The Hardy Weinberg equation is a very important concept in population genetics. Suppose we have two "alleles" for a specific trait (like eye color, gender, etc..) The proportion for which allele is present is given by  and
and 
Then by Hardy-Weinberg:
 , where both
, where both  and
and  are non-negative.
are non-negative.
Which statement discribes the graph that would appropriately represents the above relation?
Information about the Hardy Weinberg equation: http://www.nature.com/scitable/definition/hardy-weinberg-equation-299
The Hardy Weinberg equation is a very important concept in population genetics. Suppose we have two "alleles" for a specific trait (like eye color, gender, etc..) The proportion for which allele is present is given by 
Then by Hardy-Weinberg:



Which statement discribes the graph that would appropriately represents the above relation?
Tap to see back →
The equation can be reduced by taking the square root of both sides.


As a simple test, all other values when substituted into the original equation fail. However,  works. Therefore
works. Therefore  is our answer.
is our answer.
The equation can be reduced by taking the square root of both sides.
As a simple test, all other values when substituted into the original equation fail. However, 

Which of the trigonometric functions is represented by this graph?

Which of the trigonometric functions is represented by this graph?

Tap to see back →
This graph is the graph of y = csc x. The domain of this function is all real numbers except  where n is any integer. In other words, there are vertical asymptotes at all multiples of
where n is any integer. In other words, there are vertical asymptotes at all multiples of  . The range of this function is
. The range of this function is  . The period of this function is
. The period of this function is  .
.
This graph is the graph of y = csc x. The domain of this function is all real numbers except 



Which of the following functions is represented by this graph?

Which of the following functions is represented by this graph?

Tap to see back →
This graph is the graph of y = cot x. The domain of this function is all real numbers except  where n is any integer. In other words, there are vertical asymptotes at all multiples of
where n is any integer. In other words, there are vertical asymptotes at all multiples of  . The range of this function is
. The range of this function is  . The period of this function is
. The period of this function is  .
.
This graph is the graph of y = cot x. The domain of this function is all real numbers except 



Which of the following functions is represented by this graph?

Which of the following functions is represented by this graph?

Tap to see back →
This graph is the graph of y = sec x. The domain of this function is all real numbers except  where n is any integer. In other words, there are vertical asymptotes at
where n is any integer. In other words, there are vertical asymptotes at  ,
,  ,
,  , and so on. The range of this function is
, and so on. The range of this function is  . The period of this function is
. The period of this function is 
This graph is the graph of y = sec x. The domain of this function is all real numbers except 




Which of the following functions has a y-intercept of  ?
?
Which of the following functions has a y-intercept of 
Tap to see back →
The y-intercept of a function is found by substituting  . When we do this to each, we can determine the y-intercept. Don't forget your unit circle!
. When we do this to each, we can determine the y-intercept. Don't forget your unit circle!





Thus, the function with a y-intercept of  is
is  .
.
The y-intercept of a function is found by substituting 
Thus, the function with a y-intercept of 

Which of the following functions is represented by this graph?

Which of the following functions is represented by this graph?

Tap to see back →
This graph is the graph of y = cos x. The domain of this function is all real numbers. The range of this function is  . The period of this function is
. The period of this function is  .
.
This graph is the graph of y = cos x. The domain of this function is all real numbers. The range of this function is 

Which of the following functions is represented by this graph?

Which of the following functions is represented by this graph?

Tap to see back →
This graph is the graph of y = sin x. The domain of this function is all real numbers. The range of this function is  . The period of this function is
. The period of this function is  .
.
This graph is the graph of y = sin x. The domain of this function is all real numbers. The range of this function is 

True or false: If you translate a secant function  units to the left along the x-axis, you will have a cosecant curve.
units to the left along the x-axis, you will have a cosecant curve.
True or false: If you translate a secant function 
Tap to see back →
This is false. While the graphs of secant and cosecant functions are related, in order to turn a secant function into a cosecant function, you'd need to translate the original graph  units to the right to obtain a cosecant graph.
units to the right to obtain a cosecant graph.
This is false. While the graphs of secant and cosecant functions are related, in order to turn a secant function into a cosecant function, you'd need to translate the original graph 












 /|B|
/|B|



