Double Integrations on Plane - Multivariable Calculus
Card 0 of 20
Convert the following into spherical coordinates.



Convert the following into spherical coordinates.
Tap to see back →
In order to convert to spherical coordinates , we need to remember the conversion equations.



Now lets apply this to our problem.



In order to convert to spherical coordinates , we need to remember the conversion equations.
Now lets apply this to our problem.
Evaluate  , where
, where  is the trapezoidal region with vertices given by
is the trapezoidal region with vertices given by  ,
,  ,
, 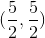 , and
, and  ,
,
using the transformation  , and
, and 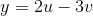 .
.
Evaluate 



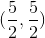

using the transformation 
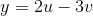
Tap to see back →
The first thing we have to do is figure out the general equations for the lines that create the trapezoid.




Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.












So our region is a rectangle given by  ,
, 
Next we need to calculate the Jacobian.

Now we can put the integral together.

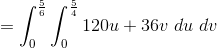

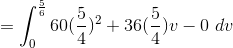



The first thing we have to do is figure out the general equations for the lines that create the trapezoid.
Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.
So our region is a rectangle given by 
Next we need to calculate the Jacobian.
Now we can put the integral together.
Convert the following into spherical coordinates.



Convert the following into spherical coordinates.
Tap to see back →
In order to convert to spherical coordinates , we need to remember the conversion equations.



Now lets apply this to our problem.



In order to convert to spherical coordinates , we need to remember the conversion equations.
Now lets apply this to our problem.
Calculate the following Integral.

Calculate the following Integral.
Tap to see back →

Lets deal with the inner integral first.




Now we evaluate this expression in the outer integral.







Lets deal with the inner integral first.
Now we evaluate this expression in the outer integral.
Calculate the following Integral.

Calculate the following Integral.
Tap to see back →

Lets deal with the inner integral first.




Now we evaluate this expression in the outer integral.







Lets deal with the inner integral first.
Now we evaluate this expression in the outer integral.
Convert the following into spherical coordinates.



Convert the following into spherical coordinates.
Tap to see back →
In order to convert to spherical coordinates , we need to remember the conversion equations.



Now lets apply this to our problem.



In order to convert to spherical coordinates , we need to remember the conversion equations.
Now lets apply this to our problem.
Evaluate  , where
, where  is the trapezoidal region with vertices given by
is the trapezoidal region with vertices given by  ,
,  ,
, 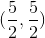 , and
, and  ,
,
using the transformation  , and
, and 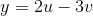 .
.
Evaluate 



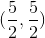

using the transformation 
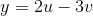
Tap to see back →
The first thing we have to do is figure out the general equations for the lines that create the trapezoid.




Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.












So our region is a rectangle given by  ,
, 
Next we need to calculate the Jacobian.

Now we can put the integral together.

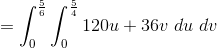

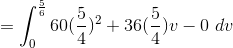



The first thing we have to do is figure out the general equations for the lines that create the trapezoid.
Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.
So our region is a rectangle given by 
Next we need to calculate the Jacobian.
Now we can put the integral together.
Convert the following into spherical coordinates.



Convert the following into spherical coordinates.
Tap to see back →
In order to convert to spherical coordinates , we need to remember the conversion equations.



Now lets apply this to our problem.



In order to convert to spherical coordinates , we need to remember the conversion equations.
Now lets apply this to our problem.
Calculate the following Integral.

Calculate the following Integral.
Tap to see back →

Lets deal with the inner integral first.




Now we evaluate this expression in the outer integral.







Lets deal with the inner integral first.
Now we evaluate this expression in the outer integral.
Calculate the following Integral.

Calculate the following Integral.
Tap to see back →

Lets deal with the inner integral first.




Now we evaluate this expression in the outer integral.







Lets deal with the inner integral first.
Now we evaluate this expression in the outer integral.
Convert the following into spherical coordinates.



Convert the following into spherical coordinates.
Tap to see back →
In order to convert to spherical coordinates , we need to remember the conversion equations.



Now lets apply this to our problem.



In order to convert to spherical coordinates , we need to remember the conversion equations.
Now lets apply this to our problem.
Evaluate  , where
, where  is the trapezoidal region with vertices given by
is the trapezoidal region with vertices given by  ,
,  ,
, 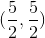 , and
, and  ,
,
using the transformation  , and
, and 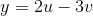 .
.
Evaluate 



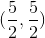

using the transformation 
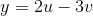
Tap to see back →
The first thing we have to do is figure out the general equations for the lines that create the trapezoid.




Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.












So our region is a rectangle given by  ,
, 
Next we need to calculate the Jacobian.

Now we can put the integral together.

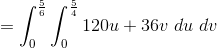

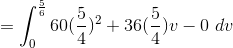



The first thing we have to do is figure out the general equations for the lines that create the trapezoid.
Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.
So our region is a rectangle given by 
Next we need to calculate the Jacobian.
Now we can put the integral together.
Convert the following into spherical coordinates.



Convert the following into spherical coordinates.
Tap to see back →
In order to convert to spherical coordinates , we need to remember the conversion equations.



Now lets apply this to our problem.



In order to convert to spherical coordinates , we need to remember the conversion equations.
Now lets apply this to our problem.
Calculate the following Integral.

Calculate the following Integral.
Tap to see back →

Lets deal with the inner integral first.




Now we evaluate this expression in the outer integral.







Lets deal with the inner integral first.
Now we evaluate this expression in the outer integral.
Calculate the following Integral.

Calculate the following Integral.
Tap to see back →

Lets deal with the inner integral first.




Now we evaluate this expression in the outer integral.







Lets deal with the inner integral first.
Now we evaluate this expression in the outer integral.
Convert the following into spherical coordinates.



Convert the following into spherical coordinates.
Tap to see back →
In order to convert to spherical coordinates , we need to remember the conversion equations.



Now lets apply this to our problem.



In order to convert to spherical coordinates , we need to remember the conversion equations.
Now lets apply this to our problem.
Evaluate  , where
, where  is the trapezoidal region with vertices given by
is the trapezoidal region with vertices given by  ,
,  ,
, 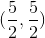 , and
, and  ,
,
using the transformation  , and
, and 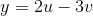 .
.
Evaluate 



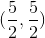

using the transformation 
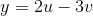
Tap to see back →
The first thing we have to do is figure out the general equations for the lines that create the trapezoid.




Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.












So our region is a rectangle given by  ,
, 
Next we need to calculate the Jacobian.

Now we can put the integral together.

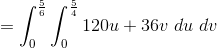

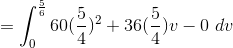



The first thing we have to do is figure out the general equations for the lines that create the trapezoid.
Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.
So our region is a rectangle given by 
Next we need to calculate the Jacobian.
Now we can put the integral together.
Convert the following into spherical coordinates.



Convert the following into spherical coordinates.
Tap to see back →
In order to convert to spherical coordinates , we need to remember the conversion equations.



Now lets apply this to our problem.



In order to convert to spherical coordinates , we need to remember the conversion equations.
Now lets apply this to our problem.
Calculate the following Integral.

Calculate the following Integral.
Tap to see back →

Lets deal with the inner integral first.




Now we evaluate this expression in the outer integral.







Lets deal with the inner integral first.
Now we evaluate this expression in the outer integral.
Calculate the following Integral.

Calculate the following Integral.
Tap to see back →

Lets deal with the inner integral first.




Now we evaluate this expression in the outer integral.







Lets deal with the inner integral first.
Now we evaluate this expression in the outer integral.