Trigonometric Functions and Graphs - Math

Card 0 of 116

Simplify the function below:

Tap to see back →

We need to use the following formulas:

a)

and

b)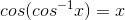

We can simplify as follows:

Which of the following is not in the range of the function $y = $\sin{x}$$ ?

Tap to see back →

The range of the function $y= \sin x$ is all numbers between and (the sine wave never goes above or below this).

Of the choices given, $\frac{3}{2}$ is greater than and thus not in this range.

What is the period of

$\tan \left ( $\frac{x}{\pi }$ \right )$ ?

Tap to see back →

The period for $\tan(x)$ is $\pi$ . However, if a number is multiplied by , you divide the period $\pi$ by what is being multiplied by . Here, $(1/\pi )$ is being multiplied by . $\pi/(1/\pi )$ equals .

Which of the given functions has the greatest amplitude?

Tap to see back →

The amplitude of a function is the amount by which the graph of the function travels above and below its midline. When graphing a sine function, the value of the amplitude is equivalent to the value of the coefficient of the sine. Similarly, the coefficient associated with the x-value is related to the function's period. The largest coefficient associated with the sine in the provided functions is 2; therefore the correct answer is $2\sin(x)$ .

The amplitude is dictated by the coefficient of the trigonometric function. In this case, all of the other functions have a coefficient of one or one-half.

What is the amplitude of $y=3\sin(2x+5)$ ?

Tap to see back →

The amplitude of a wave function like $y=3\sin(2x+5)$ is always going to be the coefficient of the function. In this case, that is .

What is the local maximum of $\sin(2x)$ between $-\pi$ and $\pi$ ?

Tap to see back →

The fastest way to solve this problem is to graph it and observe the answer. However, the other option is to think of this equation in terms of period.

When the coefficient of the variable increases, the frequency increases and the period decreases by that rate.

Since our equation is $\sin(2x)$ , our period will be $\frac{1}{2}$ the normal period of a $\sin(x)$ wave. Since only the period is changing, the amplitude is not. Therefore the amplitude (the highest and lowest points) of $\sin(2x)$ will be the same as that of $\sin(x)$ . The amplitude of a sine wave is , so the amplitude of $\sin(2x)$ will also be .

Therefore, our maximum will be .

Simplify the following trionometric function:

Tap to see back →

To solve the problem, you need to know the following information:

Replace the trigonometric functions with these values:

$$\frac{4(\frac{3}{4}$)-(1)}{($\frac{3\sqrt{2}$}{2})}$

$$\frac{2}{(\frac{3\sqrt{2}$}{2})}$

$$\frac{4}{3\sqrt{2}$} = $\frac{4\cdot \sqrt{2}$}{3$\sqrt{2}$\cdot $\sqrt{2}$} = $\frac{4\sqrt{2}$}{6} = $\frac{2\sqrt{2}$}{3}$

Change a angle to radians.

Tap to see back →

In order to change an angle into radians, you must multiply the angle by $$\frac{\pi $}{180^{\circ}$$}$ .

Therefore, to solve:

Simplify the following trigonometric function in fraction form:

Tap to see back →

To determine the value of the expression, you must know the following trigonometric values:

$sin $(30^{\circ}$)=\frac{1}{2}$$

Replacing these values, we get:

$$\frac{2}{4}$-$\frac{1}{2}$=\frac{1}{2}$-$\frac{1}{2}$=0$

If $cos\ x=\frac{1}{3}$$ and $sin\ x\neq 0$ , give the value of $\frac{sin\ x+sin\ 2x}{sin\ x-sin\ 2x}$ .

Tap to see back →

Based on the double angle formula we have, $sin\ 2x=2(sin\ x)(cos\ x)$ .

$\frac{sin\ x+sin\ 2x}{sin\ x-sin\ 2x}$=\frac{sin\ x+2(sin\ x)(cos\ x)}{sin\ x-2(sin\ x)(cos\ x)}$

$=\frac{sinx(1+2cos\ x )}{sinx(1-2cos\ x )}$=\frac{1+2cos\ x}{1-2cos\ x}$$

$=\frac{1+2(\frac{1}{3}$)}{1-2($\frac{1}{3}$)}=\frac{\frac{3+2}{3}$}{$\frac{3-2}{3}$}=5$

If $x=\frac{\pi}{3}$$ , give the value of $\frac{sin\ x}{sin\ x+cos\ 2x}$ .

Tap to see back →

$x=\frac{\pi}{3}$\Rightarrow sin\ x=sin($\frac{\pi}{3}$)=\frac{\sqrt{3}$}{2}$

Now we can write:

$x=\frac{\pi}{3}$\Rightarrow 2x=2($\frac{\pi}{3}$)=\frac{2\pi}{3}$\Rightarrow cos\ 2x=cos($\frac{2\pi}{3}$)$

$=cos(\pi-$\frac{\pi}{3}$)$

$=-cos ($\frac{\pi}{3}$)$

$=-$\frac{1}{2}$$

Now we can substitute the values:

$$\frac{sin\ x}{sin\ x+cos\ 2x}$=\frac{\frac{\sqrt{3}$}{2}}{$\frac{\sqrt{3}$}{2}-$\frac{1}{2}$}=\frac{\sqrt{3}$}{$\sqrt{3}$-1}=\frac{\sqrt{3}$}{$\sqrt{3}$-1}\times $\frac{{\sqrt{3}$+1}}{{$\sqrt{3}$+1}}=\frac{3+\sqrt{3}$}{2}$

If $cot\ $34^{\circ}$=1.5$ , give the value of $$\frac{2sin\ $326^{\circ}$$+3sin\ $56^{\circ}$}{cos\ $304^{\circ}$}$ .

Tap to see back →

Now we can simplify the expression as follows:

$$\frac{2sin\ $326^{\circ}$$+3sin\ $56^{\circ}$}{cos\ $304^{\circ}$}=\frac{-2sin\ $34^{\circ}$$+3cos\ $34^{\circ}$}{sin\ $34^{\circ}$}$

$=-2+3cot\ $34^{\circ}$=-2+3\times 1.5=-2+4.5=2.5$

If $sin\ x\times cos\ x=\frac{1}{2}$$ , what is the value of $(sin\ x+cos\ $x)^2$$ ?

Tap to see back →

$(sin\ x+cos\ $x)^2$$=sin^2x$$+cos^2x$+2sin\x cos\ x$

$=1+2(sin\ x)(cos\ x)=1+2($\frac{1}{2}$)=1+1=2$

If , give the value of .

Tap to see back →

We know that .

Simplify:

Tap to see back →

We know that .

Then we can write:

$\Rightarrow $A=\frac{(cos^2x$$-sin^2x$$)}{cos^2x$$}$+tan^2x$$

$tan (x)sin(x) + sec(x)(cos $x)^{2}$ =$

Tap to see back →

$tan (x)sin(x) + sec(x)(cos $x)^{2}$ =$

$$\frac{sin (x)}{cos (x)}$* sin(x) + $\frac{1}{cos (x)}$*(cos $x)^{2}$ =$

$$\frac{(sin $x)^{2}$$ + (cos $x)^{2}$}{cos (x)} = $\frac{1}{cos (x)}$ = sec (x)$

Simplify the following expression:

$A=cos($\frac{3\pi}{2}$+x)+sin (\pi+x)+cos($\frac{\pi}{2}$+x)+sin(\pi-x)$

Tap to see back →

We need to use the following identities:

$cos($\frac{3\pi}{2}$+x)=sin\ x$

$sin (\pi+x)=-sin\ x$

$cos($\frac{\pi}{2}$+x)=-sin\ x$

$sin(\pi-x)=sin\ x$

Use these to simplify the expression as follows:

$A=cos($\frac{3\pi}{2}$+x)+sin (\pi+x)+cos($\frac{\pi}{2}$+x)+sin(\pi-x)$

$\Rightarrow A=sin\ x-sin\ x-sin\ x+sin\ x = 0$

Simplify the trigonometric expression.

$\frac{\tan(\theta)\csc(\theta)}{\sec(\theta)}$

Tap to see back →

Using basic trigonometric identities, we can simplify the problem to

$$\frac{\frac{\sin(\theta)}{\cos(\theta)}$$\frac{1}{\sin(\theta)}$}{$\frac{1}{\cos(\theta)}$}$ .

We can cancel the sine in the numerator and the one over cosine cancels on top and bottom, leaving us with 1.

$$\frac{\frac{\sin(\theta)}{\cos(\theta)}$$\frac{1}{\sin(\theta)}$}{$\frac{1}{\cos(\theta)}$}=\frac{\frac{1}{\cos(\theta)}$}{$\frac{1}{\cos(\theta)}$}=\frac{1}{\cos(\theta)}$\cdot $\frac{\cos(\theta)}{1}$=1$

Give the value of :

$A=\frac{2sin(\frac{\pi}{2}$)+4cos($\frac{\pi}{2}$)}{4sin($\frac{\pi}{2}$)-cos($\frac{\pi}{2}$)}$

Tap to see back →

$sin($\frac{\pi}{2}$)=1$

$cos($\frac{\pi}{2}$)=0$

Plug these values in:

$A=\frac{2sin(\frac{\pi}{2}$)+4cos($\frac{\pi}{2}$)}{4sin($\frac{\pi}{2}$)-cos($\frac{\pi}{2}$)}=\frac{2\times 1+4\times 0}{4\times 1-0}$=\frac{2}{4}$=\frac{1}{2}$=0.5$

If $tan\ x = $\frac{1}{4}$$ , solve for

$D=\frac{sin\ x}{sin\ x-cos\ x}$+\frac{sin\ x+cos\ x}{cos\ x}$$

Tap to see back →

$tan\ x=\frac{1}{4}$\Rightarrow $\frac{sin\ x}{cos\ x}$=\frac{1}{4}$\Rightarrow cos\ x=4sin\ x$

Substitute $cos\ x=4sin \ x$ into the expression:

$D=\frac{sin\ x}{sin\ x-cos\ x}$+\frac{sin\ x+cos\ x}{cos\ x}$=\frac{sin\ x}{sin\ x-4sin\ x}$+\frac{sin\ x+4sin\ x}{4sin\ x}$$

$\Rightarrow D=\frac{sin\ x}{-3sin\ x}$+\frac{5sin\ x}{4sin\ x}$$

$\Rightarrow D=-$\frac{1}{3}$+\frac{5}{4}$=\frac{-4+15}{12}$=\frac{11}{12}$$