Trigonometry - Math
Card 0 of 796
Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate 
.
Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate
Tap to see back →
The altitude perpendicular to the hypotenuse of a right triangle divides that triangle into two smaller triangles similar to each other and the large triangle. Therefore, the sides are in proportion. The hypotenuse of the triangle is equal to
Therefore, we can set up, and solve for 
in, a proportion statement involving the shorter side and hypotenuse of the large triangle and the larger of the two smaller triangles:
This is not one of the choices.
The altitude perpendicular to the hypotenuse of a right triangle divides that triangle into two smaller triangles similar to each other and the large triangle. Therefore, the sides are in proportion. The hypotenuse of the triangle is equal to
Therefore, we can set up, and solve for
This is not one of the choices.
What is the length of the diagonals of trapezoid 
? Assume the figure is an isoceles trapezoid.
What is the length of the diagonals of trapezoid
Tap to see back →
To find the length of the diagonal, we need to use the Pythagorean Theorem. Therefore, we need to sketch the following triangle within trapezoid 
:
We know that the base of the triangle has length 
. By subtracting the top of the trapezoid from the bottom of the trapezoid, we get:
Dividing by two, we have the length of each additional side on the bottom of the trapezoid:
Adding these two values together, we get 
.
The formula for the length of diagonal 
uses the Pythagoreon Theorem:
, where 
is the point between 
and 
representing the base of the triangle.
Plugging in our values, we get:
To find the length of the diagonal, we need to use the Pythagorean Theorem. Therefore, we need to sketch the following triangle within trapezoid
We know that the base of the triangle has length
Dividing by two, we have the length of each additional side on the bottom of the trapezoid:
Adding these two values together, we get
The formula for the length of diagonal
Plugging in our values, we get:
Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate the length of the hypotenuse of the blue triangle.
Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate the length of the hypotenuse of the blue triangle.
Tap to see back →
The inscribed rectangle is a 20 by 20 square. Since opposite sides of the square are parallel, the corresponding angles of the two smaller right triangles are congruent; therefore, the two triangles are similar and, by definition, their sides are in proportion.
The small top triangle has legs 10 and 20. Therefore, the length of its hypotenuse can be determined using the Pythagorean Theorem:
The small top triangle has short leg 10 and hypotenuse 
. The blue triangle has short leg 20 and unknown hypotenuse 
, where 
can be calculated with the proportion statement
The inscribed rectangle is a 20 by 20 square. Since opposite sides of the square are parallel, the corresponding angles of the two smaller right triangles are congruent; therefore, the two triangles are similar and, by definition, their sides are in proportion.
The small top triangle has legs 10 and 20. Therefore, the length of its hypotenuse can be determined using the Pythagorean Theorem:
The small top triangle has short leg 10 and hypotenuse
Which of the following describes a triangle with sides one kilometer, 100 meters, and 100 meters?
Which of the following describes a triangle with sides one kilometer, 100 meters, and 100 meters?
Tap to see back →
One kilometer is equal to 1,000 meters, so the triangle has sides of length 100, 100, and 1,000. However,
That is, the sum of the least two sidelengths is not greater than the third. This violates the Triangle Inequality, and this triangle cannot exist.
One kilometer is equal to 1,000 meters, so the triangle has sides of length 100, 100, and 1,000. However,
That is, the sum of the least two sidelengths is not greater than the third. This violates the Triangle Inequality, and this triangle cannot exist.
Note: figure NOT drawn to scale.
Refer to the triangle in the above diagram.
.
Evaluate 
.
Note: figure NOT drawn to scale.
Refer to the triangle in the above diagram.
Evaluate
Tap to see back →
By the Law of Sines,
Substitute 
and solve for 
:
By the Law of Sines,
Substitute
Note: figure NOT drawn to scale.
Refer to the triangle in the above diagram.
Evaluate 
. Round to the nearest tenth, if applicable.
Note: figure NOT drawn to scale.
Refer to the triangle in the above diagram.
Evaluate
Tap to see back →
By the Law of Cosines,
Substitute 
:
By the Law of Cosines,
Substitute
The above figure is a regular pentagon. Evaluate 
to the nearest tenth.
The above figure is a regular pentagon. Evaluate
Tap to see back →
Two sides of the triangle formed measure 4 each; the included angle is one angle of the regular pentagon, which measures
The length of the third side can be found by applying the Law of Cosines:
where 
:
Two sides of the triangle formed measure 4 each; the included angle is one angle of the regular pentagon, which measures
The length of the third side can be found by applying the Law of Cosines:
where
In triangle 
, 
and 
.
Which of the following statements is true about the lengths of the sides of 
?
In triangle
Which of the following statements is true about the lengths of the sides of
Tap to see back →
In a triangle, the shortest side is opposite the angle of least measure; the longest side is opposite the angle of greatest measure. Therefore, if we order the angles, we can order their opposite sides similarly.
Since the measures of the three interior angles of a triangle must total 
,
has the least degree measure, so its opposite side, 
, is the shortest. 
, so by the Isosceles Triangle Theorem, their opposite sides 
and 
are congruent. Therefore, the correct choice is
.
In a triangle, the shortest side is opposite the angle of least measure; the longest side is opposite the angle of greatest measure. Therefore, if we order the angles, we can order their opposite sides similarly.
Since the measures of the three interior angles of a triangle must total
Assume quadrilateral 
is a rhombus. The perimeter of 
is 
, and the length of one of its diagonals is 
. What is the area of 
?
Assume quadrilateral
Tap to see back →
To solve for the area of the rhombus 
, we must use the equation 
, where 
and 
are the diagonals of the rhombus. Since the perimeter of the rhombus is 
, and by definition all 4 sides of a rhombus have the same length, we know that the length of each side is 
. We can find the length of the other diagonal if we recognize that the two diagonals combined with a side edge form a right triangle. The length of the hypotenuse is 
, and each leg of the triangle is equal to one-half of each diagonal. We can therefore set up an equation involving Pythagorean's Theorem as follows:
, where 
is equal to one-half the length of the unknown diagonal.
We can therefore solve for 
as follows:
is therefore equal to 8, and our other diagonal is 16. We can now use both diagonals to solve for the area of the rhombus:
The area of rhombus 
is therefore equal to 
To solve for the area of the rhombus
We can therefore solve for
The area of rhombus
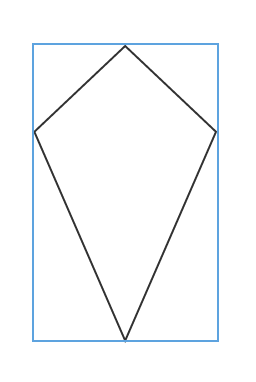
The area of the rectangle is 
, what is the area of the kite?
The area of the rectangle is
Tap to see back →
The area of a kite is half the product of the diagonals.
The diagonals of the kite are the height and width of the rectangle it is superimposed in, and we know that because the area of a rectangle is base times height.
Therefore our equation becomes:
.
We also know the area of the rectangle is 
. Substituting this value in we get the following:
Thus,, the area of the kite is 
.
The area of a kite is half the product of the diagonals.
The diagonals of the kite are the height and width of the rectangle it is superimposed in, and we know that because the area of a rectangle is base times height.
Therefore our equation becomes:
We also know the area of the rectangle is
Thus,, the area of the kite is
is a rhombus with side length 
. Diagonal 
has a length of 
. Find the length of diagonal 
.
Tap to see back →
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.
Thus, we can consider the right triangle 
to find the length of diagonal 
. From the problem, we are given that the sides are 
and 
. Because the diagonals bisect each other, we know:
Using the Pythagorean Theorem,
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.
Thus, we can consider the right triangle
Using the Pythagorean Theorem,
is a rhombus. 
and 
. Find 
.
Tap to see back →
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.
Thus, we can consider the right triangle 
to find the length of diagonal 
. From the problem, we are given that the sides are 
and 
. Because the diagonals bisect each other, we know:
Using the Pythagorean Theorem,
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.
Thus, we can consider the right triangle
Using the Pythagorean Theorem,
is rhombus with side lengths in meters. 
and 
. What is the length, in meters, of 
?
Tap to see back →
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.
Thus, we can consider the right triangle to find the length of diagonal . From the given information, each of the sides of the rhombus measures 
meters and 
.
Because the diagonals bisect each other, we know:
Using the Pythagorean theorem,
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.
Thus, we can consider the right triangle
Because the diagonals bisect each other, we know:
Using the Pythagorean theorem,
is a rhombus. 
and 
. Find the length of the sides.
Tap to see back →
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.
Thus, we can consider the right triangle to find the length of side 
. From the problem, we are given 
and 
. Because the diagonals bisect each other, we know:
Using the Pythagorean Theorem,
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.
Thus, we can consider the right triangle
Using the Pythagorean Theorem,
A kite has two perpendicular interior diagonals. One diagonal has a measurement of 
and the area of the kite is 
. Find the length of the other interior diagonal.
A kite has two perpendicular interior diagonals. One diagonal has a measurement of
Tap to see back →
This problem can be solved by applying the area formula:
Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Thus the solution is:
This problem can be solved by applying the area formula:
Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Thus the solution is:
Using the kite shown above, find the length of the red (vertical) diagonal.
Using the kite shown above, find the length of the red (vertical) diagonal.
Tap to see back →
In order to solve this problem, first observe that the red diagonal line divides the kite into two triangles that each have side lengths of 
and 
Notice, the hypotenuse of the interior triangle is the red diagonal. Therefore, use the Pythagorean theorem: 
, where 
the length of the red diagonal.
The solution is:
In order to solve this problem, first observe that the red diagonal line divides the kite into two triangles that each have side lengths of
The solution is:
A kite has two perpendicular interior diagonals. One diagonal has a measurement of 
and the area of the kite is 
. Find the sum of the two perpendicular interior diagonals.
A kite has two perpendicular interior diagonals. One diagonal has a measurement of
Tap to see back →
You must find the length of the missing diagonal before you can find the sum of the two perpendicular diagonals.
To find the missing diagonal, apply the area formula:
This question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Therefore, the sum of the two diagonals is:
You must find the length of the missing diagonal before you can find the sum of the two perpendicular diagonals.
To find the missing diagonal, apply the area formula:
This question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Therefore, the sum of the two diagonals is:
The area of the kite shown above is 
and the red diagonal has a length of 
. Find the length of the black (horizontal) diagonal.
The area of the kite shown above is
Tap to see back →
To find the length of the black diagonal apply the area formula:
Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Thus the solution is:
To find the length of the black diagonal apply the area formula:
Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Thus the solution is:
Find the length of the diagonals of this isosceles trapezoid, with 
.
Find the length of the diagonals of this isosceles trapezoid, with
Tap to see back →
To find the length of the diagonals, split the top side into 3 sections as shown below:
The two congruent sections plus 8 adds to 14. 
, so the two congruent sections add to 6. They must each be 3. This means that the top of the right triangle with the diagonal as a hypotenuse must be 11, since 
.
We can solve for the diagonal, now pictured, using Pythagorean Theorem:
take the square root of both sides
To find the length of the diagonals, split the top side into 3 sections as shown below:
The two congruent sections plus 8 adds to 14.
We can solve for the diagonal, now pictured, using Pythagorean Theorem:
Find the length of both diagonals of this quadrilateral.
Find the length of both diagonals of this quadrilateral.
Tap to see back →
All of the lengths with one mark have length 5, and all of the side lengths with two marks have length 4. With this knowledge, we can add side lengths together to find that one diagonal is the hypotenuse to this right triangle:
Using Pythagorean Theorem gives:
take the square root of each side
Similarly, the other diagonal can be found with this right triangle:
Once again using Pythagorean Theorem gives an answer of 
All of the lengths with one mark have length 5, and all of the side lengths with two marks have length 4. With this knowledge, we can add side lengths together to find that one diagonal is the hypotenuse to this right triangle:
Using Pythagorean Theorem gives:
Similarly, the other diagonal can be found with this right triangle:
Once again using Pythagorean Theorem gives an answer of