Right Triangles - Math
Card 0 of 1788
What is the hypotenuse of a right triangle with sides 5 and 8?
What is the hypotenuse of a right triangle with sides 5 and 8?
Tap to see back →
Because this is a right triangle, we can use the Pythagorean Theorem which says _a_2 + _b_2 = _c_2, or the squares of the two sides of a right triangle must equal the square of the hypotenuse. Here we have a = 5 and b = 8.
_a_2 + _b_2 = _c_2
52 + 82 = _c_2
25 + 64 = _c_2
89 = _c_2
c = √89
Because this is a right triangle, we can use the Pythagorean Theorem which says _a_2 + _b_2 = _c_2, or the squares of the two sides of a right triangle must equal the square of the hypotenuse. Here we have a = 5 and b = 8.
_a_2 + _b_2 = _c_2
52 + 82 = _c_2
25 + 64 = _c_2
89 = _c_2
c = √89
Which is the greater quantity?
(a) The hypotenuse of a right triangle with legs 
and 
.
(b) The hypotenuse of a right triangle with legs 
and 
.
Which is the greater quantity?
(a) The hypotenuse of a right triangle with legs
(b) The hypotenuse of a right triangle with legs
Tap to see back →
The hypotenuses of the triangles measure as follows:
(a) 
(b) 
, so 
, making (a) the greater quantity.
The hypotenuses of the triangles measure as follows:
(a)
(b)
Which is the greater quantity?
(a) The hypotenuse of a 
right triangle with a leg of length 20
(b) The hypotenuse of a right triangle with legs of length 19 and 21
Which is the greater quantity?
(a) The hypotenuse of a
(b) The hypotenuse of a right triangle with legs of length 19 and 21
Tap to see back →
The hypotenuses of the triangles measure as follows:
(a) 
(b) 
, so 
, making (b) the greater quantity
The hypotenuses of the triangles measure as follows:
(a)
(b)
A right triangle has a leg 
feet long and a hypotenuse 
feet long. Which is the greater quantity?
(a) The length of the second leg of the triangle
(b) 60 inches
A right triangle has a leg
(a) The length of the second leg of the triangle
(b) 60 inches
Tap to see back →
The length of the second leg can be calculated using the Pythagorean Theorem. Set 
:
The second leg therefore measures 
inches.
The length of the second leg can be calculated using the Pythagorean Theorem. Set
The second leg therefore measures
What is the hypotenuse of a right triangle with sides 9 inches and 12 inches?
What is the hypotenuse of a right triangle with sides 9 inches and 12 inches?
Tap to see back →
Since we're dealing with right triangles, we can use the Pythagorean Theorem (
). In this formula, a and b are the sides, while c is the hypotenuse. The hypotenuse of a right triangle is the longest side and the side that is opposite the right angle. Now, we can plug into our formula, which looks like this: 
We simplify and get 
. At this point, isolate c. This means taking the square root of both sides so that your answer is 15in.
Since we're dealing with right triangles, we can use the Pythagorean Theorem (
The perimeter of a regular pentagon is 75% of that of the triangle in the above diagram. Which is the greater quantity?
(A) The length of one side of the pentagon
(B) One and one-half feet
The perimeter of a regular pentagon is 75% of that of the triangle in the above diagram. Which is the greater quantity?
(A) The length of one side of the pentagon
(B) One and one-half feet
Tap to see back →
By the Pythagorean Theorem, the hypotenuse of the right triangle is
inches, making its perimeter
inches.
The pentagon in question has sides of length 75% of 112, or
.
Since a pentagon has five sides of equal length, each side will have measure
inches.
One and a half feet are equivalent to 
inches, so (B) is the greater quantity.
By the Pythagorean Theorem, the hypotenuse of the right triangle is
The pentagon in question has sides of length 75% of 112, or
Since a pentagon has five sides of equal length, each side will have measure
One and a half feet are equivalent to
The track at Gauss High School is unusual in that it is shaped like a right triangle, as shown above.
Cary decides to get some exercise by running from point A to point B, then running half of the distance from point B to point C.
Which is the greater quantity?
(A) The distance Cary runs
(B) One-fourth of a mile
The track at Gauss High School is unusual in that it is shaped like a right triangle, as shown above.
Cary decides to get some exercise by running from point A to point B, then running half of the distance from point B to point C.
Which is the greater quantity?
(A) The distance Cary runs
(B) One-fourth of a mile
Tap to see back →
By the Pythagorean Theorem, the distance from B to C is
feet
Cary runs
feet
Since 5,280 feet make a mile, one-fourth of a mile is equal to
feet.
(B) is greater
By the Pythagorean Theorem, the distance from B to C is
Cary runs
Since 5,280 feet make a mile, one-fourth of a mile is equal to
(B) is greater
Give the length of the hypotenuse of the above right triangle in terms of 
.
Give the length of the hypotenuse of the above right triangle in terms of
Tap to see back →
If we let 
be the length of the hypotenuse, then by the Pythagorean theorem,
If we let
In Square 
. 
is the midpoint of 
, 
is the midpoint of 
, and 
is the midpoint of 
. Construct the line segments 
and 
.
Which is the greater quantity?
(a) 
(b) 
In Square
Which is the greater quantity?
(a)
(b)
Tap to see back →
The figure referenced is below:
For the sake of simplicity, assume that the square has sides of length 4. The following reasoning is independent of the actual lengths, and the reason for choosing 4 will become apparent in the explanation.
and 
are midpoints of their respective sides, so 
, making 
the hypotenuse of a triangle with legs of length 2 and 2. Therefore,
.
Also, 
, and since 
is the midpoint of 
, 
. 
, making 
the hypotenuse of a triangle with legs of length 1 and 4. Therefore,
, so 
The figure referenced is below:
For the sake of simplicity, assume that the square has sides of length 4. The following reasoning is independent of the actual lengths, and the reason for choosing 4 will become apparent in the explanation.
Also,
Figure NOT drawn to scale.
In the above figure, 
is a right angle.
What is the length of 
?
Figure NOT drawn to scale.
In the above figure,
What is the length of
Tap to see back →
The altitude of a right triangle from the vertex of its right angle divides the triangle into two smaller triangles each similar to the larger triangle. In particular,
.
Their corresponding sides are in proportion, so, setting the ratios of the hypotenuses to the short legs equal to each other,
The altitude of a right triangle from the vertex of its right angle divides the triangle into two smaller triangles each similar to the larger triangle. In particular,
Their corresponding sides are in proportion, so, setting the ratios of the hypotenuses to the short legs equal to each other,
Figure NOT drawn to scale.
In the above figure, 
is a right angle.
What is the length of 
?
Figure NOT drawn to scale.
In the above figure,
What is the length of
Tap to see back →
The altitude of a right triangle from the vertex of its right angle divides the triangle into two smaller triangles each similar to the larger triangle. In particular,
.
Their corresponding sides are in proportion, so, setting the ratios of the long legs to the short legs equal to each other,
By the Pythagorean Theorem.
The proportion statement becomes
The altitude of a right triangle from the vertex of its right angle divides the triangle into two smaller triangles each similar to the larger triangle. In particular,
Their corresponding sides are in proportion, so, setting the ratios of the long legs to the short legs equal to each other,
By the Pythagorean Theorem.
The proportion statement becomes
Given: 
with 
, 
, 
.
Which is the greater quantity?
(a) 
(b) 
Given:
Which is the greater quantity?
(a)
(b)
Tap to see back →
The measure of the angle formed by the two shorter sides of a triangle can be determined to be acute, right, or obtuse by comparing the sum of the squares of those lengths to the square of the length of the opposite side. We compare:
; it follows that 
is obtuse, and has measure greater than 
The measure of the angle formed by the two shorter sides of a triangle can be determined to be acute, right, or obtuse by comparing the sum of the squares of those lengths to the square of the length of the opposite side. We compare:
Figure NOT drawn to scale.
In the above figure, is a right angle.
What is the length of ?
Figure NOT drawn to scale.
In the above figure,
What is the length of
Tap to see back →
The altitude of a right triangle from the vertex of its right angle divides the triangle into two smaller triangles each similar to the larger triangle. In particular,
.
Their corresponding sides are in proportion, so, setting the ratios of the hypotenuses to the short legs equal to each other,
The altitude of a right triangle from the vertex of its right angle divides the triangle into two smaller triangles each similar to the larger triangle. In particular,
Their corresponding sides are in proportion, so, setting the ratios of the hypotenuses to the short legs equal to each other,
Refer to the above right triangle. Which of the following is equal to 
?
Refer to the above right triangle. Which of the following is equal to
Tap to see back →
By the Pythagorean Theorem,
By the Pythagorean Theorem,
Given 
with right angle 
, 
Which is the greater quantity?
(a) 
(b) 
Given
Which is the greater quantity?
(a)
(b)
Tap to see back →
The sum of the measures of the angles of a triangle is 
, so:
This is a 
triangle, so its legs 
and 
are congruent. The quantities are equal.
The sum of the measures of the angles of a triangle is , so:
This is a
Give the length of one leg of an isosceles right triangle whose area is the same as the right triangle in the above diagram.
Give the length of one leg of an isosceles right triangle whose area is the same as the right triangle in the above diagram.
Tap to see back →
The area of a triangle is half the product of its height and its base; in a right triangle, the legs, being perpendicular, can serve as these quantites.
The triangle in the diagram has area
square inches.
An isosceles right triangle has two legs of the same length, which we will call 
. The area of that triangle, which is the same as that of the one in the diagram, is therefore
inches.
The area of a triangle is half the product of its height and its base; in a right triangle, the legs, being perpendicular, can serve as these quantites.
The triangle in the diagram has area
An isosceles right triangle has two legs of the same length, which we will call
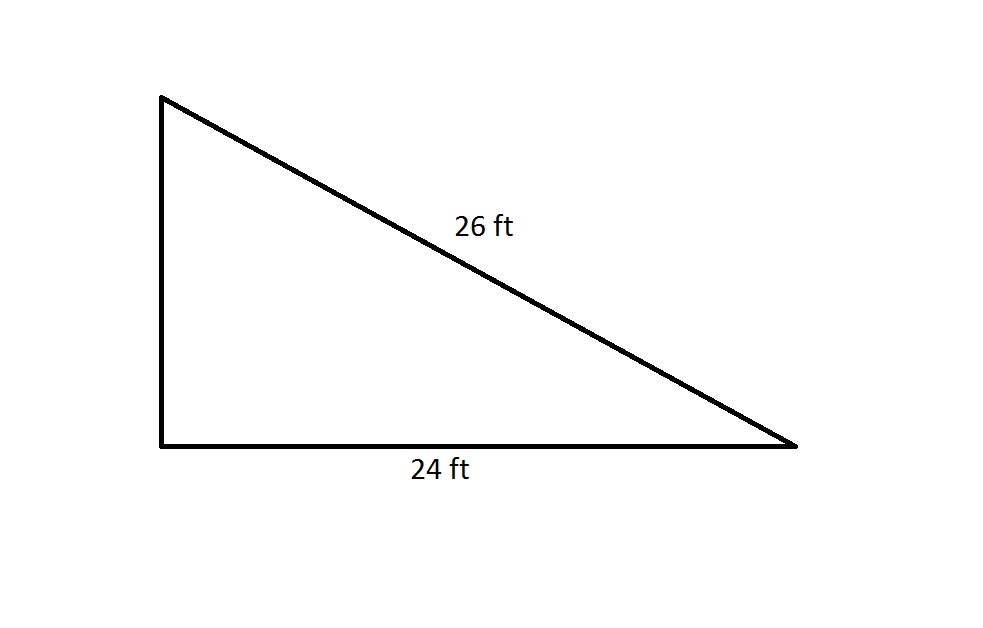
The perimeter of a regular octagon is 20% greater than that of the above right triangle. Which is the greater quantity?
(A) The length of one side of the octagon
(B) 3 yards
The perimeter of a regular octagon is 20% greater than that of the above right triangle. Which is the greater quantity?
(A) The length of one side of the octagon
(B) 3 yards
Tap to see back →
By the Pythagorean Theorem, the shorter leg has length
feet.
The perimeter of the right triangle is therefore
feet.
The octagon has perimeter 20% greater than this, or
feet.
A regular octagon has eight sides of equal length, so each side of this octagon has length
feet, which is equal to 3 yards. This makes the quantities equal.
By the Pythagorean Theorem, the shorter leg has length
The perimeter of the right triangle is therefore
The octagon has perimeter 20% greater than this, or
A regular octagon has eight sides of equal length, so each side of this octagon has length
The area of a square is equal to that of the above right triangle. Which is the greater quantity?
(A) The sidelength of the square
(B) 4 yards
The area of a square is equal to that of the above right triangle. Which is the greater quantity?
(A) The sidelength of the square
(B) 4 yards
Tap to see back →
By the Pythagorean Theorem, the shorter leg has length
feet.
The area of a triangle is equal to half the product of its base and height; for a right triangle, the legs can serve as these. The area of the above right triangle is
square feet.
The sidelength is the square root of this; 
, so 
. Therefore each sidelength of the square is just under 11 feet. 4 yards is 12 feet, so (B) is greater.
By the Pythagorean Theorem, the shorter leg has length
The area of a triangle is equal to half the product of its base and height; for a right triangle, the legs can serve as these. The area of the above right triangle is
The sidelength is the square root of this;
Consider a triangle, 
, in which 
, 
, and 
. Which is the greater quantity?
(a) 55
(b) 
Consider a triangle,
(a) 55
(b)
Tap to see back →
Suppose 
.
By the Converse of the Pythagorean Theorem, a triangle is right if and only if the sum of the squares of the lengths of the smallest two sides is equal to the square of the longest side. Compare the quantities 
and 
Therefore, if 
, so 
is right, with the right angle opposite longest side 
. Thus, 
is right and has degree measure 90.
However, 
has degree measure greater than 90, so, as a consequence of the Converse of the Pythagorean Theorem and the SAS Inequality Theorem, it holds that 
.
Suppose
By the Converse of the Pythagorean Theorem, a triangle is right if and only if the sum of the squares of the lengths of the smallest two sides is equal to the square of the longest side. Compare the quantities
Therefore, if
However,
Figure NOT drawn to scale.
Refer to the above triangle. Which is the greater quantity?
(a) 
(b) 108
Figure NOT drawn to scale.
Refer to the above triangle. Which is the greater quantity?
(a)
(b) 108
Tap to see back →
We can compare these numbers by comparing their squares.
By the Pythagorean Theorem,
Also,
, so 
.
We can compare these numbers by comparing their squares.
By the Pythagorean Theorem,
Also,