Triangles - Math
Card 0 of 464
A right triangle has a total perimeter of 12, and the length of its hypotenuse is 5. What is the area of this triangle?
A right triangle has a total perimeter of 12, and the length of its hypotenuse is 5. What is the area of this triangle?
The area of a triangle is denoted by the equation 1/2 b x h.
b stands for the length of the base, and h stands for the height.
Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.
So, 12-5 = 7 for the total perimeter of the base and height.
7 does not divide cleanly by two, but it does break down into 3 and 4,
and 1/2 (3x4) yields 6.
Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here
The area of a triangle is denoted by the equation 1/2 b x h.
b stands for the length of the base, and h stands for the height.
Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.
So, 12-5 = 7 for the total perimeter of the base and height.
7 does not divide cleanly by two, but it does break down into 3 and 4,
and 1/2 (3x4) yields 6.
Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here
Compare your answer with the correct one above
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c
Compare your answer with the correct one above
Jim leaves his home and walks 10 minutes due west and 5 minutes due south. If Jim could walk a straight line from his current position back to his house, how far, in minutes, is Jim from home?
Jim leaves his home and walks 10 minutes due west and 5 minutes due south. If Jim could walk a straight line from his current position back to his house, how far, in minutes, is Jim from home?
By using Pythagorean Theorem, we can solve for the distance “as the crow flies” from Jim to his home:
102 + 52 = _x_2
100 + 25 = _x_2
√125 = x, but we still need to factor the square root
√125 = √25*5, and since the √25 = 5, we can move that outside of the radical, so
5√5= x
By using Pythagorean Theorem, we can solve for the distance “as the crow flies” from Jim to his home:
102 + 52 = _x_2
100 + 25 = _x_2
√125 = x, but we still need to factor the square root
√125 = √25*5, and since the √25 = 5, we can move that outside of the radical, so
5√5= x
Compare your answer with the correct one above
If one of the short sides of a 45-45-90 triangle equals 5, how long is the hypotenuse?
If one of the short sides of a 45-45-90 triangle equals 5, how long is the hypotenuse?
Using the Pythagorean theorem, _x_2 + _y_2 = _h_2. And since it is a 45-45-90 triangle the two short sides are equal. Therefore 52 + 52 = _h_2 . Multiplied out 25 + 25 = _h_2.
Therefore _h_2 = 50, so h = √50 = √2 * √25 or 5√2.
Using the Pythagorean theorem, _x_2 + _y_2 = _h_2. And since it is a 45-45-90 triangle the two short sides are equal. Therefore 52 + 52 = _h_2 . Multiplied out 25 + 25 = _h_2.
Therefore _h_2 = 50, so h = √50 = √2 * √25 or 5√2.
Compare your answer with the correct one above
If the length of CB is 6 and the angle C measures 45º, what is the length of AC in the given right triangle?
If the length of CB is 6 and the angle C measures 45º, what is the length of AC in the given right triangle?
Pythagorean Theorum
AB2 + BC2 = AC2
If C is 45º then A is 45º, therefore AB = BC
AB2 + BC2 = AC2
62 + 62 = AC2
2*62 = AC2
AC = √(2*62) = 6√2
Pythagorean Theorum
AB2 + BC2 = AC2
If C is 45º then A is 45º, therefore AB = BC
AB2 + BC2 = AC2
62 + 62 = AC2
2*62 = AC2
AC = √(2*62) = 6√2
Compare your answer with the correct one above
A square enclosure has a total area of 3,600 square feet. What is the length, in feet, of a diagonal across the field rounded to the nearest whole number?
A square enclosure has a total area of 3,600 square feet. What is the length, in feet, of a diagonal across the field rounded to the nearest whole number?
In order to find the length of the diagonal accross a square, we must first find the lengths of the individual sides.
The area of a square is found by multiply the lengths of 2 sides of a square by itself.
So, the square root of 3,600 comes out to 60 ft.
The diagonal of a square can be found by treating it like a right triangle, and so, we can use the pythagorean theorem for a right triangle.
602 + 602 = C2
the square root of 7,200 is 84.8, which can be rounded to 85
In order to find the length of the diagonal accross a square, we must first find the lengths of the individual sides.
The area of a square is found by multiply the lengths of 2 sides of a square by itself.
So, the square root of 3,600 comes out to 60 ft.
The diagonal of a square can be found by treating it like a right triangle, and so, we can use the pythagorean theorem for a right triangle.
602 + 602 = C2
the square root of 7,200 is 84.8, which can be rounded to 85
Compare your answer with the correct one above
Dan drives 5 miles north and then 8 miles west to get to school. If he walks, he can take a direct path from his house to the school, cutting down the distance. How long is the path from Dan's house to his school?
Dan drives 5 miles north and then 8 miles west to get to school. If he walks, he can take a direct path from his house to the school, cutting down the distance. How long is the path from Dan's house to his school?
We are really looking for the hypotenuse of a triangle that has legs of 5 miles and 8 miles.
Apply the Pythagorean Theorem:
a2 + b2 = c2
25 + 64 = c2
89 = c2
c = 9.43 miles
We are really looking for the hypotenuse of a triangle that has legs of 5 miles and 8 miles.
Apply the Pythagorean Theorem:
a2 + b2 = c2
25 + 64 = c2
89 = c2
c = 9.43 miles
Compare your answer with the correct one above
To get from his house to the hardware store, Bob must drive 3 miles to the east and then 4 miles to the north. If Bob was able to drive along a straight line directly connecting his house to the store, how far would he have to travel then?
To get from his house to the hardware store, Bob must drive 3 miles to the east and then 4 miles to the north. If Bob was able to drive along a straight line directly connecting his house to the store, how far would he have to travel then?
Since east and north directions are perpendicular, the possible routes Bob can take can be represented by a right triangle with sides a and b of length 3 miles and 5 miles, respectively. The hypotenuse c represents the straight line connecting his house to the store, and its length can be found using the Pythagorean theorem: _c_2 = 32+ 42 = 25. Since the square root of 25 is 5, the length of the hypotenuse is 5 miles.
Since east and north directions are perpendicular, the possible routes Bob can take can be represented by a right triangle with sides a and b of length 3 miles and 5 miles, respectively. The hypotenuse c represents the straight line connecting his house to the store, and its length can be found using the Pythagorean theorem: _c_2 = 32+ 42 = 25. Since the square root of 25 is 5, the length of the hypotenuse is 5 miles.
Compare your answer with the correct one above
A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?
A right triangle has legs of 15m and 20m. What is the length of the hypotenuse?
The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.
(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m
The Pythagorean theorem is a2 + b2 = c2, where a and b are legs of the right triangle, and c is the hypotenuse.
(15)2 + (20)2 = c2 so c2 = 625. Take the square root to get c = 25m
Compare your answer with the correct one above
Which of the following sets of line-segment lengths can form a triangle?
Which of the following sets of line-segment lengths can form a triangle?
In any given triangle, the sum of any two sides is greater than the third. The incorrect answers have the sum of two sides equal to the third.
In any given triangle, the sum of any two sides is greater than the third. The incorrect answers have the sum of two sides equal to the third.
Compare your answer with the correct one above
An isosceles triangle has a base of 6 and a height of 4. What is the perimeter of the triangle?
An isosceles triangle has a base of 6 and a height of 4. What is the perimeter of the triangle?
An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).
The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).
5 + 5 + 6 = 16
An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).
The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).
5 + 5 + 6 = 16
Compare your answer with the correct one above
The base of a right isosceles triangle is 8 inches. The hypotenuse is not the base. What is the area of the triangle in inches?
The base of a right isosceles triangle is 8 inches. The hypotenuse is not the base. What is the area of the triangle in inches?
To find the area of a triangle, multiply the base by the height, then divide by 2. Since the short legs of an isosceles triangle are the same length, we need to know only one to know the other. Since, a short side serves as the base of the triangle, the other short side tells us the height.
To find the area of a triangle, multiply the base by the height, then divide by 2. Since the short legs of an isosceles triangle are the same length, we need to know only one to know the other. Since, a short side serves as the base of the triangle, the other short side tells us the height.
Compare your answer with the correct one above
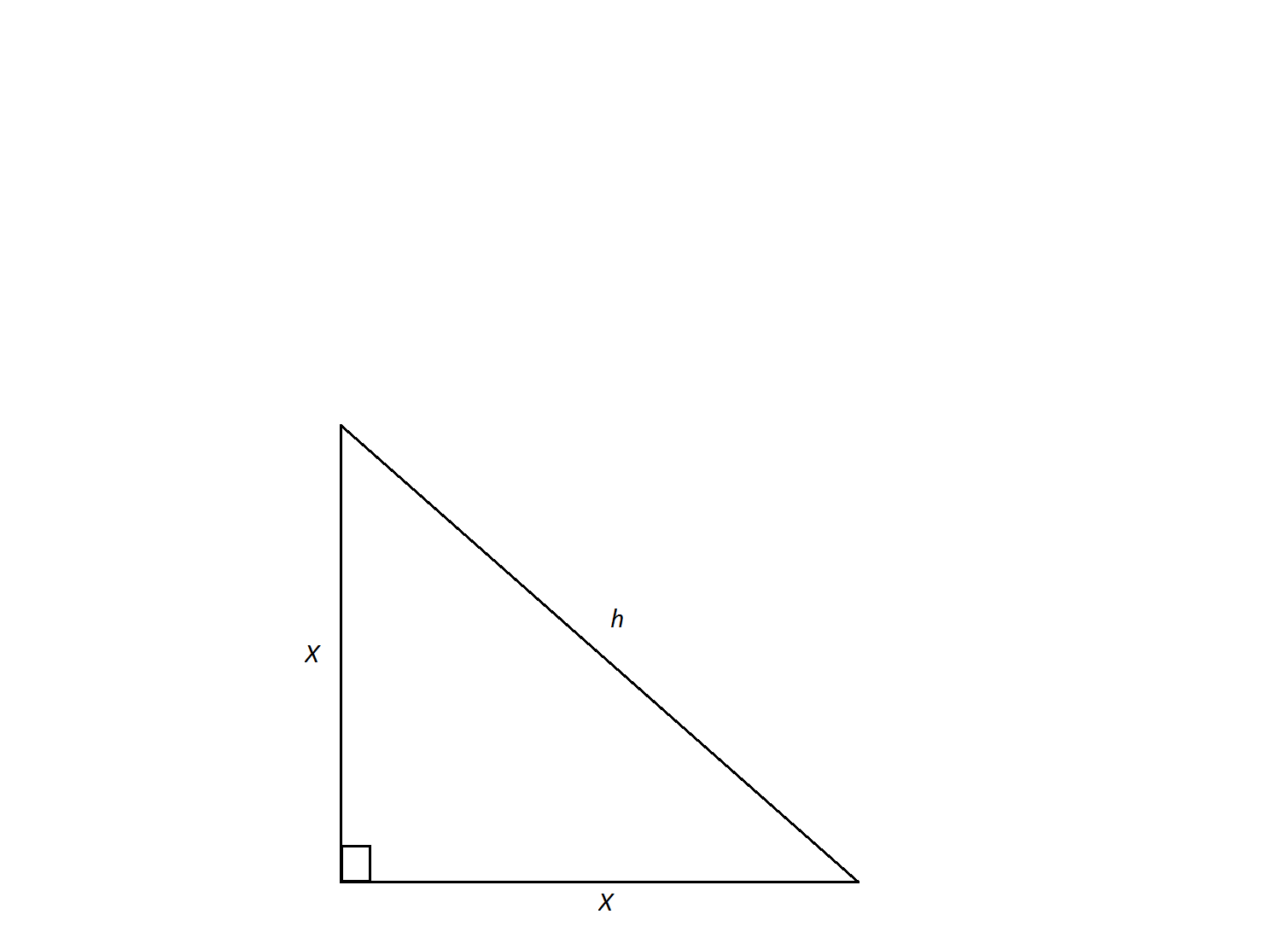
An isosceles right triangle has a hypotenuse of 
. Find its area.
An isosceles right triangle has a hypotenuse of
In order to calculate the triangle's area, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
triangles and their side lengths follow a specific pattern that states that one can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2.
Now we can calculate the area using the formula
Now, convert to feet.
In order to calculate the triangle's area, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as
Now we can calculate the area using the formula
Now, convert to feet.
Compare your answer with the correct one above
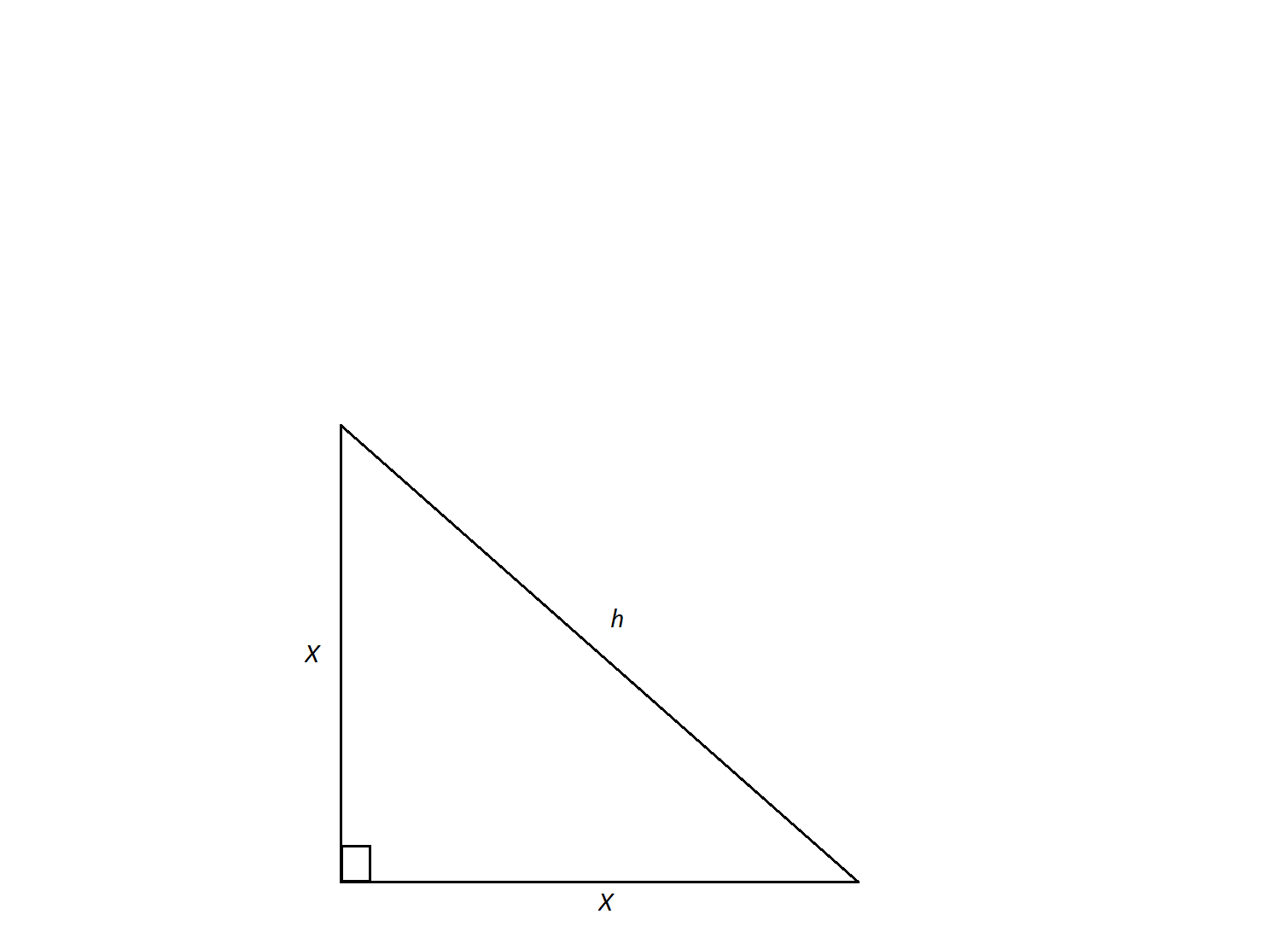
In an isosceles right triangle, two sides equal 
. Find the length of side 
.
In an isosceles right triangle, two sides equal
This problem represents the definition of the side lengths of an isosceles right triangle. By definition the sides equal 
, 
, and 
. However, if you did not remember this definition one can also find the length of the side using the Pythagorean theorem 
.
This problem represents the definition of the side lengths of an isosceles right triangle. By definition the sides equal
Compare your answer with the correct one above
ABCD is a square whose side is 
units. Find the length of diagonal AC.
ABCD is a square whose side is
To find the length of the diagonal, given two sides of the square, we can create two equal triangles from the square. The diagonal line splits the right angles of the square in half, creating two triangles with the angles of 
, 
, and 
degrees. This type of triangle is a special right triangle, with the relationship between the side opposite the 
degree angles serving as x, and the side opposite the 
degree angle serving as 
.
Appyling this, if we plug 
in for 
we get that the side opposite the right angle (aka the diagonal) is 
To find the length of the diagonal, given two sides of the square, we can create two equal triangles from the square. The diagonal line splits the right angles of the square in half, creating two triangles with the angles of
Appyling this, if we plug
Compare your answer with the correct one above
The area of a square is 
. Find the length of the diagonal of the square.
The area of a square is
If the area of the square is 
, we know that each side of the square is 
, because the area of a square is 
.
Then, the diagonal creates two 
special right triangles. Knowing that the sides = 
, we can find that the hypotenuse (aka diagonal) is 
If the area of the square is
Then, the diagonal creates two
Compare your answer with the correct one above
What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
Compare your answer with the correct one above
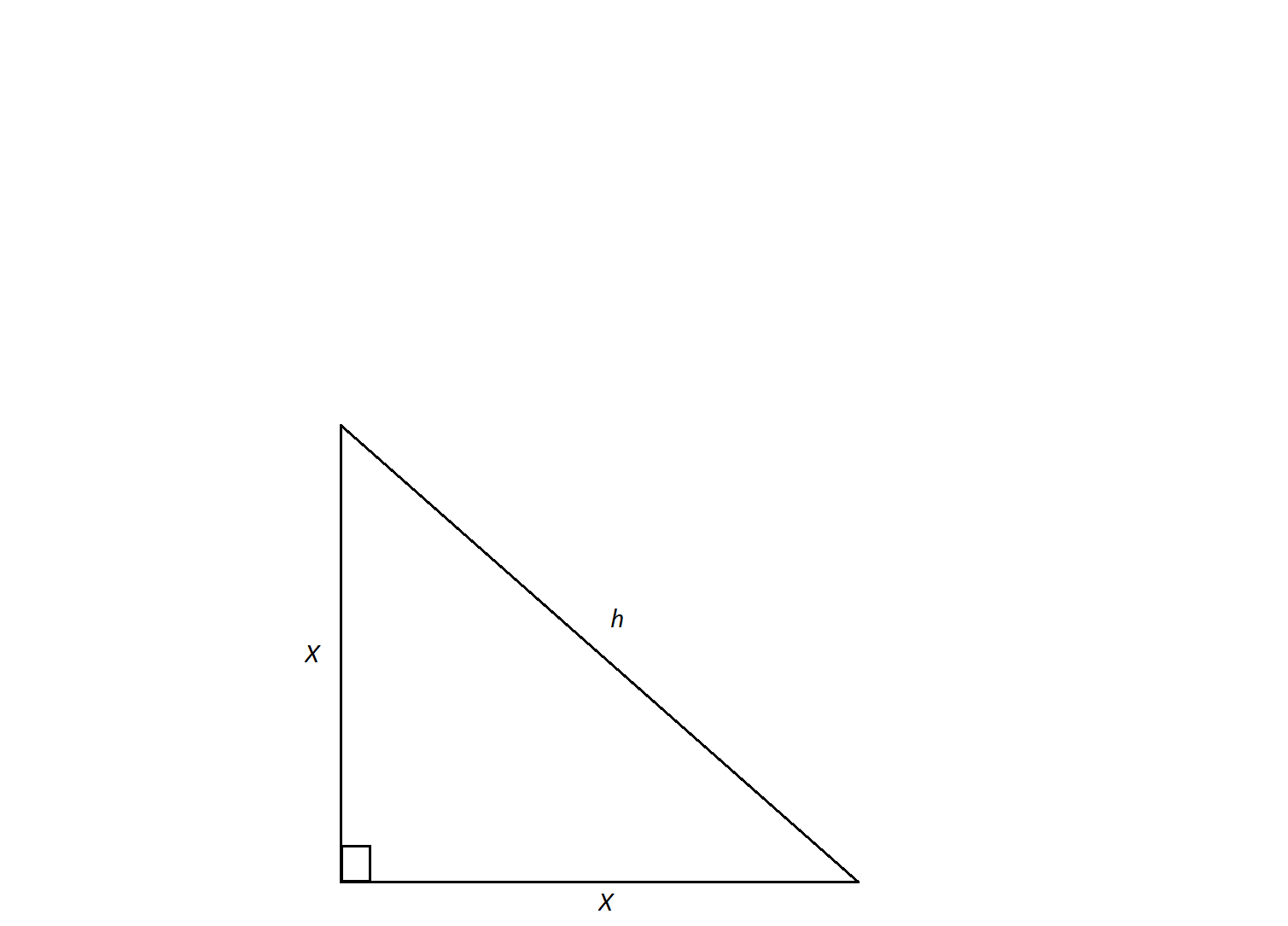
An isosceles triangle has a hypotenuse of 
. Find the length of its sides, 
.
An isosceles triangle has a hypotenuse of
An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
triangles and their side lengths follow a specific pattern that states you can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2
An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as
Compare your answer with the correct one above
The measure of the sides of this isosceles right triangle are 
. Find the measure of its hypotenuse,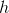 
.
The measure of the sides of this isosceles right triangle are
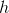
An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
triangles and their side lenghts follow a specific pattern that states you can calculate the length of the hypotenuse of an isoceles triangle by multiplying the length of one of the legs by the square root of 2.
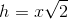
An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as
Compare your answer with the correct one above
The hypotenuse of an isosceles right triangle has a measure of 
. Find its perimeter.
The hypotenuse of an isosceles right triangle has a measure of
In order to calculate the triangle's perimeter, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
triangles and their side lengths follow a specific pattern that states that one can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2.
Now we can calculate the perimeter by doubling 
and adding 
.
In order to calculate the triangle's perimeter, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as
Now we can calculate the perimeter by doubling
Compare your answer with the correct one above