Whole Numbers - Math
Card 0 of 208

Simplify:
Simplify:
Tap to see back →
Combine like terms:  . Remember you can only combine terms that have the same variables, for example
. Remember you can only combine terms that have the same variables, for example  and
and  , but not
, but not  and
and 
Combine like terms: 



Simplify the expression below.

Simplify the expression below.
Tap to see back →
First, distribute the negative sign into the parentheses.

Next, combine like terms.

Note that all operations in this problem are addition and subtraction; there is no need to FOIL or multiply.
First, distribute the negative sign into the parentheses.
Next, combine like terms.
Note that all operations in this problem are addition and subtraction; there is no need to FOIL or multiply.
What is  simplified?
simplified?
What is 
Tap to see back →
To simplify a problem like the example above we must combine the like termed variables.
Like terms are the numbers that have the same variable, in this example,  and
and  .
.
Separate the  's to get
's to get  .
.
Then perform the necessary subtraction to get  .
.
Then separate the  's to get
's to get  .
.
Then perform the necessary subtraction to get  .
.
We then combine our answers to have the simplified version of the equation  .
.
To simplify a problem like the example above we must combine the like termed variables.
Like terms are the numbers that have the same variable, in this example, 

Separate the 

Then perform the necessary subtraction to get 
Then separate the 

Then perform the necessary subtraction to get 
We then combine our answers to have the simplified version of the equation 
Simplify the expression.

Simplify the expression.
Tap to see back →

Re-write the expression to group like terms together.

Simplify.

Re-write the expression to group like terms together.
Simplify.
What is  simplified?
simplified?
What is 
Tap to see back →
To simplify a problem like the example above we must combine the like termed variables.
Like terms are the numbers that have the same variable, in this example,  and
and 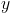 .
.
Separate the  's to get
's to get  .
.
Then perform the necessary subtraction and addition with the numbers in front of the variables to get  or
or  .
.
Then separate the 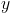 ’s to get
’s to get  .
.
Then perform the necessary subtraction to get  .
.
We then combine our answers to have the simplified version of the equation  .
.
To simplify a problem like the example above we must combine the like termed variables.
Like terms are the numbers that have the same variable, in this example, and
.
Separate the 's to get

Then perform the necessary subtraction and addition with the numbers in front of the variables to get 

Then separate the ’s to get

Then perform the necessary subtraction to get 
We then combine our answers to have the simplified version of the equation 
What is  simplified?
simplified?
What is 
Tap to see back →
To simplify a problem like the example above we must combine the like-termed variables.
Like terms are the terms that share the same variable(s) to the same power. In this example the like term is  .
.
To combine like terms the variable  stays the same and you add the numbers in front.
stays the same and you add the numbers in front.
Perform the necessary addition,  , to get
, to get  .
.
We have the simplified version of the equation,  .
.
To simplify a problem like the example above we must combine the like-termed variables.
Like terms are the terms that share the same variable(s) to the same power. In this example the like term is 
To combine like terms the variable 
Perform the necessary addition, 

We have the simplified version of the equation, 
Simplify the following equation into its simplest form by combining like terms:

Simplify the following equation into its simplest form by combining like terms:
Tap to see back →
When combining like terms, the order of operations must also be taken into account.

then combine the x squared terms to get the answer.
When combining like terms, the order of operations must also be taken into account.
then combine the x squared terms to get the answer.
Tap to see back →
When you multiply exponents you can simply add the exponents:

When you multiply exponents you can simply add the exponents:
Evaluate the exponential expression.

Evaluate the exponential expression.
Tap to see back →
We can solve this problem in two different ways.
The first way is to evaluate the internal term,  , and then square it.
, and then square it.


The second method is to use the power rule of exponents, where we multiply the exponents and solve the resulting term.


We can solve this problem in two different ways.
The first way is to evaluate the internal term, 
The second method is to use the power rule of exponents, where we multiply the exponents and solve the resulting term.
Evaluate  .
.
Evaluate 
Tap to see back →
The negative sign in the exponent indicates that in order to solve you should use the reciprocal of the integer.



The negative sign in the exponent indicates that in order to solve you should use the reciprocal of the integer.
Evaluate the term.

Evaluate the term.
Tap to see back →

A negative exponent can be written as a positive exponent in the denominator of a fraction.

Now we can evaluate the exponent and simplify.

A negative exponent can be written as a positive exponent in the denominator of a fraction.
Now we can evaluate the exponent and simplify.
Evaluate 
Evaluate
Tap to see back →
The laws of exponents state that when a number is raised to a certain power and then raised to another power then the exponents are multiplied by one another.

Solve for the exponents.


Therefore,


The laws of exponents state that when a number is raised to a certain power and then raised to another power then the exponents are multiplied by one another.
Solve for the exponents.
Therefore,
What is 
What is
Tap to see back →
When a number is raised to a power it means that the number is multiplied by itself the same number of times as the number of the power.
In this case  is raised to the
is raised to the  power so it is equivalent to
power so it is equivalent to 
We then perform the necessary multiplication to arrive at the answer of  .
.
When a number is raised to a power it means that the number is multiplied by itself the same number of times as the number of the power.
In this case 

We then perform the necessary multiplication to arrive at the answer of 
Tap to see back →
When a number is raised to a power it means that the number is multiplied by itself the same number of times as the number of the power.
In this case  is raised to the
is raised to the  power so it is equivalent to
power so it is equivalent to 
We then perform the necessary multiplication to arrive at the answer of  .
.
When a number is raised to a power it means that the number is multiplied by itself the same number of times as the number of the power.
In this case 

We then perform the necessary multiplication to arrive at the answer of 
Convert to standard notation.

Convert to standard notation.
Tap to see back →
Because the exponent is negative, we have to move the decimal four places to the left. We need to add three zeroes between the decimal the number three.

Because the exponent is negative, we have to move the decimal four places to the left. We need to add three zeroes between the decimal the number three.
Simplify the fractional expression.

Simplify the fractional expression.
Tap to see back →
Simplifying exponents with a common base can be done by subtracting the exponent in the denominator from the exponent in the numerator.


This gives us the final answer,  .
.
Simplifying exponents with a common base can be done by subtracting the exponent in the denominator from the exponent in the numerator.
This gives us the final answer, 
Tap to see back →
Even though the base of the exponents are the same, you cannot add the exponents. You must perform each exponent separately.



Even though the base of the exponents are the same, you cannot add the exponents. You must perform each exponent separately.
Tap to see back →
Since the two bases of the exponents are the same and are being multiplied, it is acceptable to combine the terms and add their exponents resulting in  which equals 128.
which equals 128.
Since the two bases of the exponents are the same and are being multiplied, it is acceptable to combine the terms and add their exponents resulting in 
What is  ?
?
What is 
Tap to see back →
When you see an exponent, remember it just means the number times itself that many times. That means that  is just another way to write
is just another way to write  .
.
From here, we can solve it all together in a calculator, or do it in pieces on our own.



When you see an exponent, remember it just means the number times itself that many times. That means that 

From here, we can solve it all together in a calculator, or do it in pieces on our own.
What is  ?
?
What is 
Tap to see back →
Remember, an exponent just means the number times itself that many times.
That means that  is just another way to write
is just another way to write  . From here, we can solve.
. From here, we can solve.


Remember, an exponent just means the number times itself that many times.
That means that 




