Circles - Math

Card 0 of 2896

The clock in the classroom reads 5:00pm. What is the angle that the hands are forming?

Tap to see back →

Since the clock is a circle, you can determine that the total number of degrees inside the circle is 360. Since a clock has 12 numbers, we can divide 360 by 12 to see what the angle is between two numbers that are right next to each other. Thus, we can see that the angle between two numbers right next to each other is . However, the clock is reading 5:00, so there are five numbers we have to take in to account. Therefore, we multiply 30 by 5, which gives us as our answer.

The time on a clock reads 5:00. What is the measure of the central angle formed by the hands of the clock?

Tap to see back →

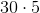First, remember that the number of degrees in a circle is 360. Then, figure out how many degrees are in between each number on the face of the clock. Since there are 12 numbers, there are between each number. Since the time reads 5:00, multiply $30\cdot 5$ , which yields .

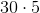
The track at Truman High School is shown above; it is comprised of a square and a semicircle.

Veronica begins at Point A, runs three times around the track counterclockwise, and continues until she reaches Point B. Which of the following comes closest to the distance Veronica runs?

Tap to see back →

First, it is necessary to know the length of the semicircle connecting Points B and D, which has diameter 500 feet; this length is about

$$\frac{1}{2}$ C = $\frac{1}{2}$ \cdot \pi d \approx $\frac{1}{2}$ \cdot 3.14 \cdot 500 = 785$ feet.

The distance around the track is about

feet.

Veronica runs around the track three complete times, for a distance of about

$3 \times 2,285 = 6,855$ feet.

She then runs from Point A to Point E, which is another 500 feet; Point E to Point D, which is yet another 500 feet, and, finally Point D to Point B, for a final 785 feet. The total distance Veronica runs is about

feet.

Divide by 5,280 to convert to miles:

$8,640 \div5,280 \approx 1.6$

The closest answer is $1 $\frac{1}{2}$$ miles.

A giant clock has a minute hand five yards in length. Since noon, the tip of the minute hand has traveled $200 \pi$ feet. Which is the greater quantity?

(A) The amount of time that has passed since noon

(B) The amount of time until midnight

Tap to see back →

Five yards is equal to fifteen feet, which is the length of the minute hand. Subsequently, fifteen feet is the radius of the circle traveled by its tip in one hour; the circumference of this circle is $2 \pi$ times this, or

$C = 2 \pi \cdot 15 = 30 \pi$ feet.

In one six-hour period, the minute hand revolves six times, so its tip travles six times the circumference, or

$30 \pi \times 6 = 180 \pi$

The clock has traveled farther than this, so the time is later than 6:00 PM, and more time has elapsed since noon than is left until midnight. This makes (A) greater.

Compare the two quantities:

Quantity A: The area of a circle with radius

Quantity B: The circumference of a circle with radius

Tap to see back →

Recall for this question that the formulae for the area and circumference of a circle are, respectively:

$A=\pi * $r^2$$

$C=2\pir$

For our two quantities, we have:

Quantity A: $\pi * $5^2$ = 25\pi$

Quantity B: $2 * \pi * 8.1 = 16.2\pi$

Therefore, quantity A is greater.

The circumferences of eight circles form an arithmetic sequence. The smallest circle has radius two inches; the second smallest circle has radius five inches. Give the radius of the largest circle.

Tap to see back →

The circumference of a circle can be determined by multiplying its radius by $2 \pi$ , so the circumferences of the two smallest circles are

and

The circumferences form an arithmetic sequence with common difference

The circumference of a circle can therefore be found using the formula

where and $d = 6 \pi$ ; we are looking for that of the th smallest circle, so

$= 4 \pi + 7 \cdot 6 \pi$

$= 4 \pi + 42 \pi$

$= 46 \pi$

Since the radius of a circle is the circumference of the circle divided by $2 \pi$ , the radius of this eighth circle is

$r = $\frac{46 \pi}{2 \pi}$ = 23$ inches, or 1 foot 11 inches.

The track at Simon Bolivar High School is a perfect circle of radius 500 feet, and is shown in the above figure. Manuel starts at point C, runs around the track counterclockwise three times, and continues to run clockwise until he makes it to point D. Which of the following comes closest to the number of miles Manuel has run?

Tap to see back →

The circumference of a circle with radius 500 feet is

$C = 2 \pi r \approx 2 \cdot 3.14 \cdot 500 = 3,140$ feet.

Manuel runs this distance three times, then he runs from Point C to D, which is about four-fifths of this distance. Therefore, Manuel's run will be about

$3,140 \times 3 $\frac{4}{5}$ = 11,932$ feet.

Divide by 5,280 to convert to miles:

$11,932 \div 5,280 \approx 2.26$ ,

making $2$\frac{1}{4}$$ miles the response closest to the actual running distance.

The track at James Buchanan High School is shown above; it is comprised of a square and a semicircle.

Diane wants to run two miles. If she begins at Point A and begins running counterclockwise, when she is finished, which of the five points will she be closest to?

Tap to see back →

First, it is necessary to know the length of the semicircle connecting Points B and D, which has diameter 400 feet; this length is

$$\frac{1}{2}$ C = $\frac{1}{2}$ \cdot \pi d \approx $\frac{1}{2}$ \cdot 3.14 \cdot 400 = 628$ feet.

The distance around the track is about

feet.

Diane wants to run two miles, or

$5,280 \times 2 = 10, 560$ feet.

She will make about

$10,560 \div 1,828 \approx 5.78$

circuits around the track.

Equivalently, she will run the track 5 complete times for a total of about

$5 \times 1,828 = 9,140$ feet,

so she will have

feet to go.

She is running counterclockwise, so she will proceed from Point A to Point D, running another 800 feet, leaving

feet.

She will almost, but not quite, finish the 628 feet from Point D to Point B.

The correct response is Point B.

The track at Monroe High School is a perfect circle of radius 600 feet, and is shown in the above figure. Quinnella wants to run around the track for one and a half miles. If Quinnella starts at point C and runs counterclockwise, which of the following is closest to the point at which she will stop running?

(Assume the five points are evenly spaced)

Tap to see back →

A circle of radius 600 feet will have a circumference of

$C = 2 \pi r \approx 2 \cdot 3.14 \cdot 600 = 3,768$ feet.

Quinnella will run one and a half miles, or

$5,280 \times 1$\frac{1}{2}$ = 7,920$ feet,

which is about times the circumference of the circle.

Quinnella will run around the track twice, returning to Point C; she will not quite make it to Point B a third time, since that is one-fifth of the track, or 0.2. The correct response is that she will be between Points B and C.

The track at Monroe Elementary School is a perfect circle of radius 400 feet, and is shown in the above figure.

Evan and his younger brother Mike both start running from Point A. Evan runs counterclockwise, running once around the track and then on to Point E; Mike runs clockwise, meeting Evan at Point E and stopping.

Which of the following is the greater quantity?

(a) Twice Mike's average speed.

(b) Evan's average speed.

(Assume the five points are evenly spaced)

Tap to see back →

It is not actually necessary to know the radius or length of the track if we know the points are equally spaced. Evan runs once around the track counterclockwise and then on to Point E, which is the next point after A; this means he runs around the track $1$\frac{1}{5}$ = $\frac{6}{5}$$ times. Mike runs around the track clockwise from Point A to Point E, in the same time, meaning he runs around the track $\frac{4}{5}$ times.

Therefore, Evan's speed is $\frac{ \frac{6}{5}$}{$\frac{4}{5}$} = $\frac{3}{2}$ times Mike's speed. As a result, Twice Mike's speed would be greater than Evan's speed, making (b) the greater.

The track at Monroe High School is a perfect circle of radius 600 feet, and is shown in the above figure.

Jerry begins his one-mile run at Point A, then runs counterclockwise around the track. At the end of his one-mile run, which is the greater quantity?

(a) The additional distance he would have to run if he were to continue to run counterclockwise to Point A.

(b) The additional distance he would have to run if he were to turn back and run clockwise to Point A.

Tap to see back →

The circumference of a circle with radius 600 feet is

$C = 2 \pi r \approx 2 \cdot 3.14 \cdot 600 = 3,768$ feet.

A one mile run would be

$$\frac{5,280 }{3,768}$ \approx 1.4$

times the length of the track.

Therefore, Jerry's run takes him around the track once, and about 0.4 times the length of the track. Since he is running counterclockwise, but has not made it halfway around the track yet, the longer of the two paths is to proceed counterclockwise and run the remaining 0.6 of the track. This makes (a) greater.

The radii of six circles form an arithmetic sequence. The radius of the second-smallest circle is twice that of the smallest circle. Which of the following, if either, is the greater quantity?

(a) The circumference of the largest circle

(b) Twice the circumference of the third-smallest circle

Tap to see back →

Call the radius of the smallest circle . The radius of the second-smallest circle is then , and the common difference of the radii is .

The radii of the six circles are, from least to greatest:

The largest circle has circumference

The third-smallest circle has circumference:

Twice this is

$2 $C_{3}$ = 2 \cdot 6 \pi r = 12 \pi r$

The circumference of the sixth circle is equal to twice that of the third-smallest circle, so the correct choice is that that (a) and (b) are equal.

In the above figure, .

Which is the greater quantity?

(a) The sum of the circumferences of the inner and outer circles

(b) The sum of the circumferences of the second-largest and third-largest circles

Tap to see back →

For the sake of simplicity, we will assume that ; this reasoning is independent of the actual length.

The four concentric circles have radii 1, 2, 3, and 4, respectively, and their circumferences can be found by multiplying these radii by $2 \pi$ .

The inner and outer circles have circumferences $2 \pi \cdot 1 = 2 \pi$ and $2 \pi \cdot 4 =8 \pi$ , respectively; the sum of these circumferences is $2 \pi + 8 \pi = 10 \pi$ . The other two circles have circumferences $2 \pi \cdot 2 = 4 \pi$ and $2 \pi \cdot 3 =6 \pi$ ; the sum of these circumferences is $4 \pi + 6 \pi = 10 \pi$ .

The two sums are therefore equal.

Circle B has a radius $\frac{2}{3}$ as long as that of Circle A.

Which is the greater quantity?

(a) The area of Circle A

(b) Twice the area of Circle B

Tap to see back →

If we call the radius of Circle A , then the radius of Circle B is $$\frac{2}{3}$ r$ .

The areas of the circles are:

(a) $\pi $r^{2}$$

(b) $\pi \left( $\frac{2}{3}$ r \right ) ^{2} = $\frac{4}{9}$ \pi $r^{2}$$

Twice the area of Circle B is

$2 \cdot \pi \left( $\frac{2}{3}$ r \right ) ^{2} =2 \cdot $\frac{4}{9}$ \pi $r^{2}$ = $\frac{8}{9}$ \pi $r^{2}$ < \pi $r^{2}$$ ,

making (a) the greater number.

Circle 1 is inscribed inside a square. The square is inscribed inside Circle 2.

Which is the greater quantity?

(a) Twice the area of Circle 1

(b) The area of Circle 2

Tap to see back →

If the radius of Circle 1 is , then the square will have sidelength equal to the diameter of the circle, or . Circle 2 will have as its diameter the length of a diagonal of the square, which by the $45 ^{\circ }-45 ^{\circ $}-90^{\circ }$$ Theorem is $\sqrt{2}$ times that, or $2r $\sqrt{2}$$ . The radius of Circle 2 will therefore be half that, or $r $\sqrt{2}$$ .

The area of Circle 1 will be $A = \pi $r^{2}$$ . The area of Circle 2 will be $A = \pi \left ( r$\sqrt{2}$ \right ) ^{2} = \pi \left ( $r^{2}$ \cdot 2 \right ) = 2 \pi $r^{2}$$ , twice that of Circle 1.

Compare the two quantities:

Quantity A: The area of a circle with radius

Quantity B: The circumference of a circle with radius

Tap to see back →

Recall for this question that the formulae for the area and circumference of a circle are, respectively:

$A=\pi * $r^2$$

$C=2\pir$

For our two quantities, we have:

Quantity A: $\pi * $13^2$ = 169\pi$

Quantity B: $2 * \pi * 63 = 126\pi$

Therefore, quantity A is greater.

The radius of a circle is . Give the area of the circle in terms of .

Tap to see back →

The area of a circle with radius can be found using the formula

$A = \pi $r^{2}$$

Since , the area is

$A = \pi (x- $5)^{2}$$

$A = \pi $(x^{2}$ - 2 \cdot x \cdot 5 + $5^{2}$)$

$A = \pi $(x^{2}$ - 10 x + 25)$

$A = \pi $x^{2}$ - 10 \pi x +25 \pi$

The radius of a circle is . Give the circumference of the circle in terms of .

Tap to see back →

The circumference of a circle is $2 \pi$ times its radius. Therefore, since the radius is , the circumference is

$2 \pi \left (x - 5 \right ) = 2 \pi x - 2 \pi \cdot 5 = 2 \pi x - 10 \pi$

The radii of six circles form an arithmetic sequence. The radius of the second-smallest circle is twice that of the smallest circle. Which of the following, if either, is the greater quantity?

(a) The area of the largest circle

(b) Twice the area of the third-smallest circle

Tap to see back →

Call the radius of the smallest circle . The radius of the second-smallest circle is then , and the common difference of the radii is .

The radii of the six circles are, from least to greatest:

The largest circle has area

The third-smallest circle has area:

Twice this is

$2 $A_{3}$ = 2 \cdot 9 \pi $r^{2}$ = 18 \pi $r^{2}$$

The area of the sixth circle is greater than twice that of the third-smallest circle, so the correct choice is that (a) is greater.

The areas of six circles form an arithmetic sequence. The second-smallest circle has a radius twice that of the smallest circle.

Which is the greater quantity?

(a) The area of the largest circle.

(b) Twice the area of the third-largest circle.

Tap to see back →

Let be the radius of the smallest circle. Then the second-smallest circle has radius . Their areas, respectively, are

and

The areas form an arithmetic sequence, so their common difference is

$4 \pi $r^{2}$ - \pi $r^{2}$ = 3 \pi $r^{2}$$ .

The six areas are

$\pi r ^{2}, 4 \pi r ^{2}, 7 \pi r ^{2}, 10 \pi r ^{2}, 13 \pi r ^{2}, 17 \pi r ^{2}$

The third-largest circle has area $10 \pi r ^{2}$ ; twice this is $20 \pi r ^{2}$ . This is greater than the area of the largest circle, which is $17\pi r ^{2}$ . (b) is the greater quantity.