Radicals - Math
Card 0 of 376
Factor and simplify the following radical expression:

Factor and simplify the following radical expression:
Tap to see back →
Begin by multiplying the numerator and denominator by the complement of the denominator:



Combine like terms and simplify:


Begin by multiplying the numerator and denominator by the complement of the denominator:
Combine like terms and simplify:
Express the following radical in rational (exponential) form:

Express the following radical in rational (exponential) form:
Tap to see back →
To convert the radical to exponent form, begin by converting the integer:


Now, divide each exponent by  to remove the radical:
to remove the radical:

Finally, simplify the exponents:

To convert the radical to exponent form, begin by converting the integer:
Now, divide each exponent by 
Finally, simplify the exponents:
Convert the radical to exponential notation.
![\small \sqrt[4]{13}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/116532/gif.latex)
Convert the radical to exponential notation.
Tap to see back →
Remember that any term outside the radical will be in the denominator of the exponent.

Since  does not have any roots, we are simply raising it to the one-fourth power.
does not have any roots, we are simply raising it to the one-fourth power.

Remember that any term outside the radical will be in the denominator of the exponent.
Since 
What is the value of  ?
?
What is the value of 
Tap to see back →
An exponent written as a fraction can be rewritten using roots.  can be reqritten as
can be reqritten as  . The bottom number on the fraction becomes the root, and the top becomes the exponent you raise the number to.
. The bottom number on the fraction becomes the root, and the top becomes the exponent you raise the number to.  is the same as
is the same as  . This will give us the answer of 243.
. This will give us the answer of 243.
An exponent written as a fraction can be rewritten using roots. 



Express the following radical in rational (exponential) form:

Express the following radical in rational (exponential) form:
Tap to see back →
To convert the radical to exponent form, begin by converting the integer:


Now, divide each exponent by  to clear the square root:
to clear the square root:

Finally, simplify the exponents:

To convert the radical to exponent form, begin by converting the integer:
Now, divide each exponent by 
Finally, simplify the exponents:
Express the following radical in rational (exponential) form:

Express the following radical in rational (exponential) form:
Tap to see back →
To convert the radical to exponent form, begin by converting the integer:

![=\sqrt[4]{3\cdot $2^5a$^$5b^7c$^8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/152734/gif.latex)
Now, divide each exponent by  to cancel the radical:
to cancel the radical:

Finally, simplify the exponents:

To convert the radical to exponent form, begin by converting the integer:
Now, divide each exponent by 
Finally, simplify the exponents:
Which fraction is equivalent to  ?
?
Which fraction is equivalent to 
Tap to see back →
Multiply the numerator and denominator by the compliment of the denominator:

Simplify the expression:

Multiply the numerator and denominator by the compliment of the denominator:
Simplify the expression:
Simplify the following radical. Express in rational (exponential) form.

Simplify the following radical. Express in rational (exponential) form.
Tap to see back →
Multiply the numerator and denominator by the compliment of the denominator:

Simplify the expression:

Multiply the numerator and denominator by the compliment of the denominator:
Simplify the expression:
Choose the fraction equivalent to  .
.
Choose the fraction equivalent to 
Tap to see back →
Multiply the numerator and denominator by the compliment of the denominator:


Simplify the expression:

Multiply the numerator and denominator by the compliment of the denominator:

Simplify the expression:
Simplify the following radical. Express in rational (exponential) form.

Simplify the following radical. Express in rational (exponential) form.
Tap to see back →
Multiply the numerator and denominator to the exponent:


Simplify the expression by combining like terms:

Multiply the numerator and denominator to the exponent:
Simplify the expression by combining like terms:
Simplify: 
Simplify:
Tap to see back →
Multiply the numerator and denominator to the exponent:


Simplify the expression by combining like terms:

Multiply the numerator and denominator to the exponent:
Simplify the expression by combining like terms:
Express the following exponent in radical form:

Express the following exponent in radical form:
Tap to see back →
Begin by converting each exponent to have a denominator of  :
:


Now, rearrange into radical form:

Finally, simplify:

Begin by converting each exponent to have a denominator of 
Now, rearrange into radical form:
Finally, simplify:
Express the following exponent in radical form:

Express the following exponent in radical form:
Tap to see back →
Begin by converting each exponent to have a denominator of  :
:


Now, put this in radical form:

Finally, simplify:

Begin by converting each exponent to have a denominator of 
Now, put this in radical form:
Finally, simplify:
Express the following exponent in radical form:

Express the following exponent in radical form:
Tap to see back →
Begin by changing the fractional exponents so that they both have a common denominator of  :
:


Now, put this in radical form and simplify:



Begin by changing the fractional exponents so that they both have a common denominator of 
Now, put this in radical form and simplify:
Simplify the following radical expression using exponents. Express the final answer in radical form.

Simplify the following radical expression using exponents. Express the final answer in radical form.
Tap to see back →
Begin by converting the radical into exponent form:


Simplify the exponent and multiply:


Convert into radical form:

Simplify:

Begin by converting the radical into exponent form:
Simplify the exponent and multiply:
Convert into radical form:
Simplify:
Simplify the expression. Find the positive solution only.

Simplify the expression. Find the positive solution only.
Tap to see back →
When working in square roots, each component can be treated separately.

Now, we can simplify each term.


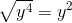
Combine the simplified terms to find the answer. Anything outside of the square root is combined, while anything under the root is combined under the root.

When working in square roots, each component can be treated separately.
Now, we can simplify each term.
Combine the simplified terms to find the answer. Anything outside of the square root is combined, while anything under the root is combined under the root.
Find the value of  .
.
Find the value of 
Tap to see back →
To solve this equation, we have to factor our radicals. We do this by finding numbers that multiply to give us the number within the radical.


Add them together:

4 is a perfect square, so we can find the root:


Since both have the same radical, we can combine them:

To solve this equation, we have to factor our radicals. We do this by finding numbers that multiply to give us the number within the radical.
Add them together:
4 is a perfect square, so we can find the root:
Since both have the same radical, we can combine them:
Simplify the expression:
![$\frac{3\sqrt[4]{32}$}{2\sqrt[4]{162}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/93697/gif.latex)
Simplify the expression:
Tap to see back →
Use the multiplication property of radicals to split the fourth roots as follows:
![\rightarrow $\frac{3\sqrt[4]{16}$\sqrt[4]{2}}{2\sqrt[4]{81}\sqrt[4]{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/93698/gif.latex)
Simplify the new roots:
![\rightarrow $\frac{3(2)\sqrt[4]{2}$}{2(3)\sqrt[4]{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/117469/gif.latex)
![\rightarrow $\frac{6\sqrt[4]{2}$}{6\sqrt[4]{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/93699/gif.latex)

Use the multiplication property of radicals to split the fourth roots as follows:
Simplify the new roots:
Factor and simplify the following radical expression:

Factor and simplify the following radical expression:
Tap to see back →
Begin by factoring the integer:



Now, simplify the exponents:



Begin by factoring the integer:
Now, simplify the exponents:
Factor and simplify the following radical expression:

Factor and simplify the following radical expression:
Tap to see back →
Begin by converting the radical into exponent form:


Now, multiply the exponents:

Begin by converting the radical into exponent form:
Now, multiply the exponents: