Absolute Value - Math
Card 0 of 336
Find the  -intercepts for the graph given by the equation:
-intercepts for the graph given by the equation:

Find the 
Tap to see back →
To find the  -intercepts, we must set
-intercepts, we must set  .
.
To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.



Now we must set up our two scenarios:
 and
and 
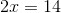 and
and 
 and
and 
To find the 

To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.
Now we must set up our two scenarios:

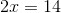

Solve for  .
.

Solve for 
Tap to see back →

Divide both sides by 3.

Consider both the negative and positive values for the absolute value term.

Subtract 2 from both sides to solve both scenarios for  .
.

Divide both sides by 3.
Consider both the negative and positive values for the absolute value term.
Subtract 2 from both sides to solve both scenarios for 
Solve for  :
:

Solve for 
Tap to see back →
To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.


and

This gives us:
 and
and 

However, this question has an  outside of the absolute value expression, in this case
outside of the absolute value expression, in this case  . Thus, any negative value of
. Thus, any negative value of  will make the right side of the equation equal to a negative number, which cannot be true for an absolute value expression. Thus,
will make the right side of the equation equal to a negative number, which cannot be true for an absolute value expression. Thus,  is an extraneous solution, as
is an extraneous solution, as  cannot equal a negative number.
cannot equal a negative number.
Our final solution is then

To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.
and
This gives us:

However, this question has an 




Our final solution is then

What are the possible values for  ?
?
What are the possible values for 
Tap to see back →
The absolute value measures the distance from zero to the given point.
In this case, since  ,
,  or
or  , as both values are twelve units away from zero.
, as both values are twelve units away from zero.
The absolute value measures the distance from zero to the given point.
In this case, since 


Tap to see back →
Solve:

Solve:
Tap to see back →
The absolute value can never be negative, so the equation is ONLY valid at zero.
The equation to solve becomes  .
.

The absolute value can never be negative, so the equation is ONLY valid at zero.
The equation to solve becomes 
Expression 1: 
Expression 2: 
Find the set of values for  where Expression 1 is greater than Expression 2.
where Expression 1 is greater than Expression 2.
Expression 1:
Expression 2:
Find the set of values for 
Tap to see back →
In finding the values for  where
where  , break the comparison of these two absolute value expressions into the four possible ways this could potentially be satisfied.
, break the comparison of these two absolute value expressions into the four possible ways this could potentially be satisfied.
The first possibility is described by the inequality:

If you think of a number line, it is evident that there is no solution to this inequality since there will never be a case where subtracting from  will lead to a greater number than adding to
will lead to a greater number than adding to  .
.
The second possibility, wherein  is negative and converted to its opposite to being an absolute value expression but
is negative and converted to its opposite to being an absolute value expression but  is positive and requires no conversion, can be represented by the inequality (where the sign is inverted due to multiplication by a negative):
is positive and requires no conversion, can be represented by the inequality (where the sign is inverted due to multiplication by a negative):

We can simplify this inequality to find that  satisfies the conditions where
satisfies the conditions where  .
.
The third possibility can be represented by the following inequality (where the sign is inverted due to multiplication by a negative):

This is again simplified to  and is redundant with the above inequality.
and is redundant with the above inequality.
The final possibility is represented by the inequality

This inequality simplifies to  . Rewriting this as
. Rewriting this as  makes it evident that this inequality is true of all real numbers. This does not provide any additional conditions on how to satisfy the original inequality.
makes it evident that this inequality is true of all real numbers. This does not provide any additional conditions on how to satisfy the original inequality.
The only possible condition that satisfies the inequality is that which arises in two of the tested cases, when  .
.
In finding the values for 

The first possibility is described by the inequality:
If you think of a number line, it is evident that there is no solution to this inequality since there will never be a case where subtracting from 

The second possibility, wherein 

We can simplify this inequality to find that 

The third possibility can be represented by the following inequality (where the sign is inverted due to multiplication by a negative):
This is again simplified to 
The final possibility is represented by the inequality
This inequality simplifies to 

The only possible condition that satisfies the inequality is that which arises in two of the tested cases, when 
What is the absolute value of -3?
What is the absolute value of -3?
Tap to see back →
The absolute value is the distance from a given number to 0. In our example, we are given -3. This number is 3 units away from 0, and thus the absolute value of -3 is 3.
If a number is negative, its absolute value will be the positive number with the same magnitude. If a number is positive, it will be its own absolute value.
The absolute value is the distance from a given number to 0. In our example, we are given -3. This number is 3 units away from 0, and thus the absolute value of -3 is 3.
If a number is negative, its absolute value will be the positive number with the same magnitude. If a number is positive, it will be its own absolute value.
An individual's heart rate during exercise is between  and
and  of the individual's maximum heart rate. The maximum heart rate of a
of the individual's maximum heart rate. The maximum heart rate of a  year old is
year old is  beats per minute. Express a
beats per minute. Express a  year old's target heart rate in an absolute value equation. Note: round the
year old's target heart rate in an absolute value equation. Note: round the  and
and  endpoints to the nearest whole number.
endpoints to the nearest whole number.
An individual's heart rate during exercise is between 






Tap to see back →
We start by finding the midpoint of the interval, which is enclosed by 60% of 204 and 80% of 204.


We find the midpoint, or average, of these endpoints by adding them and dividing by two:

142.5 is exactly 20.5 units away from both endpoints, 122 and 163. Since we are looking for the range of numbers between 122 and 163, all possible values have to be within 20.5 units of 142.5. If a number is greater than 20.5 units away from 142.5, either in the positive or negative direction, it will be outside of the \[122, 163\] interval. We can express this using absolute value in the following way:

We start by finding the midpoint of the interval, which is enclosed by 60% of 204 and 80% of 204.
We find the midpoint, or average, of these endpoints by adding them and dividing by two:
142.5 is exactly 20.5 units away from both endpoints, 122 and 163. Since we are looking for the range of numbers between 122 and 163, all possible values have to be within 20.5 units of 142.5. If a number is greater than 20.5 units away from 142.5, either in the positive or negative direction, it will be outside of the \[122, 163\] interval. We can express this using absolute value in the following way:
Solve the inequality:

Solve the inequality:
Tap to see back →
The inequality compares an absolute value function with a negative integer. Since the absolute value of any real number is greater than or equal to 0, it can never be less than a negative number. Therefore,  can never happen. There is no solution.
can never happen. There is no solution.
The inequality compares an absolute value function with a negative integer. Since the absolute value of any real number is greater than or equal to 0, it can never be less than a negative number. Therefore, 
Solve for  :
:

Solve for 
Tap to see back →
Solve for positive values by ignoring the absolute value. Solve for negative values by switching the inequality and adding a negative sign to 7.
Solve for positive values by ignoring the absolute value. Solve for negative values by switching the inequality and adding a negative sign to 7.
Give the solution set for the following equation:

Give the solution set for the following equation:
Tap to see back →
First, subtract 5 from both sides to get the absolute value expression alone.


Split this into two linear equations:



or



The solution set is 
First, subtract 5 from both sides to get the absolute value expression alone.
Split this into two linear equations:
or
The solution set is
In order to ride a certain roller coaster at an amusement park an individual needs to be between  and
and  pounds. Express this rule using an absolute value.
pounds. Express this rule using an absolute value.
In order to ride a certain roller coaster at an amusement park an individual needs to be between 

Tap to see back →
We start by finding the midpoint of the interval, which is enclosed by 90 and 210. We find the midpoint, or average, of these two endpoints by adding them and dividing by two:

150 is exactly 60 units away from both endpoints, 90 and 210. Since we are looking for the range of numbers that fall in between 90 and 210, this means that any possible value can't be more than 60 units away from 150. If a number is more than 60 units away from 150, in either the increasing or decreasing direction, it will be outside of the \[90, 210\] interval. We can express this using absolute value in the following way:

We start by finding the midpoint of the interval, which is enclosed by 90 and 210. We find the midpoint, or average, of these two endpoints by adding them and dividing by two:
150 is exactly 60 units away from both endpoints, 90 and 210. Since we are looking for the range of numbers that fall in between 90 and 210, this means that any possible value can't be more than 60 units away from 150. If a number is more than 60 units away from 150, in either the increasing or decreasing direction, it will be outside of the \[90, 210\] interval. We can express this using absolute value in the following way:
Solve for  .
.

Solve for 
Tap to see back →

Divide both sides by 3.

Consider both the negative and positive values for the absolute value term.

Subtract 2 from both sides to solve both scenarios for  .
.

Divide both sides by 3.
Consider both the negative and positive values for the absolute value term.
Subtract 2 from both sides to solve both scenarios for 
Solve for  in the inequality below.
in the inequality below.

Solve for 
Tap to see back →
The absolute value gives two problems to solve. Remember to switch the "less than" to "greater than" when comparing the negative term.
 or
or 
Solve each inequality separately by adding  to all sides.
to all sides.
 or
or 
This can be simplified to the format  .
.
The absolute value gives two problems to solve. Remember to switch the "less than" to "greater than" when comparing the negative term.

Solve each inequality separately by adding 

This can be simplified to the format 
Tap to see back →
Solve the inequality.

Solve the inequality.
Tap to see back →

Remove the absolute value by setting the term equal to either  or
or  . Remember to flip the inequality for the negative term!
. Remember to flip the inequality for the negative term!

Solve each scenario independently by subtracting  from both sides.
from both sides.


Remove the absolute value by setting the term equal to either 

Solve each scenario independently by subtracting 
Solve for  :
:

Solve for 
Tap to see back →
To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.


and

This gives us:
 and
and 

However, this question has an  outside of the absolute value expression, in this case
outside of the absolute value expression, in this case  . Thus, any negative value of
. Thus, any negative value of  will make the right side of the equation equal to a negative number, which cannot be true for an absolute value expression. Thus,
will make the right side of the equation equal to a negative number, which cannot be true for an absolute value expression. Thus,  is an extraneous solution, as
is an extraneous solution, as  cannot equal a negative number.
cannot equal a negative number.
Our final solution is then

To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.
and
This gives us:

However, this question has an 




Our final solution is then
Solve for  :
:

Solve for 
Tap to see back →
The absolute value of any number is nonnegative, so  must always be greater than
must always be greater than  . Therefore, any value of
. Therefore, any value of  makes this a true statement.
makes this a true statement.
The absolute value of any number is nonnegative, so 


Solve the following absolute value inequality:

Solve the following absolute value inequality:
Tap to see back →
To solve this inequality, it is best to break it up into two separate inequalities to eliminate the absolute value function:
 or
or  .
.
Then, solve each one separately:


Combining these solutions gives: 
To solve this inequality, it is best to break it up into two separate inequalities to eliminate the absolute value function:


Then, solve each one separately:
Combining these solutions gives:









