Finding Zeros of a Polynomial - Math
Card 0 of 92
Find the zeros of the following polynomial:

Find the zeros of the following polynomial:
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:

Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for  , we're hoping that the equation ends up equaling zero. Let's see if
, we're hoping that the equation ends up equaling zero. Let's see if  is a zero:
is a zero:
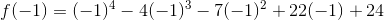


Since the function equals zero when  is
is  , one of the factors of the polynomial is
, one of the factors of the polynomial is  . This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.
. This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.



Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24) $"f(x)=(x+1)(x^{3}$$-5x^{2}$-2x+24)")
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try  :
:
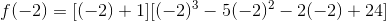

When we factor using synthetic substitution for  , we get the following result:
, we get the following result:

Using our quadratic factoring rules, we can factor completely:

Thus, the zeroes of  are
are 
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:
Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for 

Since the function equals zero when 


Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24) $"f(x)=(x+1)(x^{3}$$-5x^{2}$-2x+24)")
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try 
When we factor using synthetic substitution for 
Using our quadratic factoring rules, we can factor completely:
Thus, the zeroes of 
Compare your answer with the correct one above
Find the roots of the function:

Find the roots of the function:
Factor:


Double check by factoring:




Add together: 
Therefore:


Factor:
Double check by factoring:
Add together:
Therefore:
Compare your answer with the correct one above
Solve for x.

Solve for x.

- Split up the middle term so that factoring by grouping is possible.
Factors of 10 include:
1 * 10= 10 1 + 10 = 11
2 * 5 =10 2 + 5 = 7
–2 * –5 = 10 –2 + –5 = –7 Good!

- Now factor by grouping, pulling "x" out of the first pair and "-5" out of the second.

- Now pull out the common factor, the "(x-2)," from both terms.

- Set both terms equal to zero to find the possible roots and solve using inverse operations.
x – 5 = 0, x = 5
x – 2 = 0, x = 2
- Split up the middle term so that factoring by grouping is possible.
Factors of 10 include:
1 * 10= 10 1 + 10 = 11
2 * 5 =10 2 + 5 = 7
–2 * –5 = 10 –2 + –5 = –7 Good!
- Now factor by grouping, pulling "x" out of the first pair and "-5" out of the second.
- Now pull out the common factor, the "(x-2)," from both terms.
- Set both terms equal to zero to find the possible roots and solve using inverse operations.
x – 5 = 0, x = 5
x – 2 = 0, x = 2
Compare your answer with the correct one above
Solve for  :
:

Solve for 
To solve for  , you need to isolate it to one side of the equation. You can subtract the
, you need to isolate it to one side of the equation. You can subtract the  from the right to the left. Then you can add the 6 from the right to the left:
from the right to the left. Then you can add the 6 from the right to the left:



Next, you can factor out this quadratic equation to solve for  . You need to determine which factors of 8 add up to negative 6:
. You need to determine which factors of 8 add up to negative 6:


Finally, you set each binomial equal to 0 and solve for  :
:

To solve for 

Next, you can factor out this quadratic equation to solve for 
Finally, you set each binomial equal to 0 and solve for 
Compare your answer with the correct one above
Find the roots of  .
.
Find the roots of 
If we recognize this as an expression with form  , with
, with  and
and  , we can solve this equation by factoring:
, we can solve this equation by factoring:


 and
and 
 and
and 
If we recognize this as an expression with form 




Compare your answer with the correct one above
Find the zeros of the given polynomial:

Find the zeros of the given polynomial:
To find the values for  in which the polynomial equals
in which the polynomial equals  , we first want to factor the equation:
, we first want to factor the equation:






To find the values for 

Compare your answer with the correct one above
If the following is a zero of a polynomial, find another zero.

If the following is a zero of a polynomial, find another zero.
When finding zeros of a polynomial, you must remember your rules. Without a function this may seem tricky, but remember that non-real solutions come in conjugate pairs. Conjugate pairs differ in the middle sign. Thus, our answer is:

When finding zeros of a polynomial, you must remember your rules. Without a function this may seem tricky, but remember that non-real solutions come in conjugate pairs. Conjugate pairs differ in the middle sign. Thus, our answer is:
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Consider the polynomial

By Descartes' Rule of Signs alone, how many positive real zeroes does  have?
have?
(Note: you are not being asked for the actual number of positive real zeroes.)
Consider the polynomial
By Descartes' Rule of Signs alone, how many positive real zeroes does 
(Note: you are not being asked for the actual number of positive real zeroes.)
By Descartes' Rule of Signs, the number of sign changes - changes from positive to negative coefficient signs - in  gives the maximum number of positive real zeroes; the actual number of positive real zeroes must be that many or differ by an even number.
gives the maximum number of positive real zeroes; the actual number of positive real zeroes must be that many or differ by an even number.
If the polynomial

is examined, it can be seen that there are no changes in sign from term to term; all coefficients are positive. Therefore, there can be no positive real zeroes.
By Descartes' Rule of Signs, the number of sign changes - changes from positive to negative coefficient signs - in 
If the polynomial
is examined, it can be seen that there are no changes in sign from term to term; all coefficients are positive. Therefore, there can be no positive real zeroes.
Compare your answer with the correct one above























