Functions and Graphs - Math
Card 0 of 608
Refer to the line in the above diagram. It we were to continue to draw it so that it intersects the 
-axis, where would its 
-intercept be?
Refer to the line in the above diagram. It we were to continue to draw it so that it intersects the
Tap to see back →
First, we need to find the slope of the line.
In order to move from the lower left point to the upper right point, it is necessary to move up five units and right three units. This is a rise of 5 and a run of 3. makes the slope of the line shown 
.
We can use this to find the 
-intercept 
using the slope formula as follows:
The lower left point has coordinates 
. Therefore, we can set up and solve for 
in this slope formula, setting 
:
First, we need to find the slope of the line.
In order to move from the lower left point to the upper right point, it is necessary to move up five units and right three units. This is a rise of 5 and a run of 3. makes the slope of the line shown
We can use this to find the
The lower left point has coordinates
Determine where the graphs of the following equations will intersect.
Determine where the graphs of the following equations will intersect.
Tap to see back →
We can solve the system of equations using the substitution method.
Solve for 
in the second equation.
Substitute this value of 
into the first equation.
Now we can solve for 
.
Solve for 
using the first equation with this new value of 
.
The solution is the ordered pair 
.
We can solve the system of equations using the substitution method.
Solve for
Substitute this value of
Now we can solve for
Solve for
The solution is the ordered pair
Which of the following graphs correctly depicts the graph of the inequality 
Which of the following graphs correctly depicts the graph of the inequality
Tap to see back →
Let's start by looking at the given equation:
The inequality is written in slope-intercept form; therefore, the slope is equal to 
and the y-intercept is equal to 
.
All of the graphs depict a line with slope of 
and y-intercept 
. Next, we need to decide if we should shade above or below the line. To do this, we can determine if the statement is true using the origin 
. If the origin satisfies the inequality, we will know to shade below the line. Substitute the values into the given equation and solve.
Because this statement is true, the origin must be included in the shaded region, so we shade below the line.
Finally, a statement that is "less than" or "greater than" requires a dashed line in the graph. On the other hand, those that are "greater than or equal to" or "less than or equal to" require a solid line. We will select the graph with shading below a dashed line.
Let's start by looking at the given equation:
The inequality is written in slope-intercept form; therefore, the slope is equal to
All of the graphs depict a line with slope of
Because this statement is true, the origin must be included in the shaded region, so we shade below the line.
Finally, a statement that is "less than" or "greater than" requires a dashed line in the graph. On the other hand, those that are "greater than or equal to" or "less than or equal to" require a solid line. We will select the graph with shading below a dashed line.
Refer to the above diagram. which of the following compound inequality statements has this set of points as its graph?
Refer to the above diagram. which of the following compound inequality statements has this set of points as its graph?
Tap to see back →
A horizontal line has equation 
for some value of 
; since the line goes through a point with 
-coordinate 3, the line is 
. Also, since the line is solid and the region above this line is shaded in, the corresponding inequality is 
.
A vertical line has equation 
for some value of 
; since the line goes through a point with 
-coordinate 4, the line is 
. Also, since the line is solid and the region right of this line is shaded in, the corresponding inequality is 
.
Since only the region belonging to both sets is shaded - that is, their intersection is shaded - the statements are connected with "and". The correct choice is 
.
A horizontal line has equation
A vertical line has equation
Since only the region belonging to both sets is shaded - that is, their intersection is shaded - the statements are connected with "and". The correct choice is
Which of the following inequalities is graphed above?
Which of the following inequalities is graphed above?
Tap to see back →
First, we determine the equation of the boundary line. This line includes points 
and 
, so the slope can be calculated as follows:
Since we also know the 
-intercept is 
, we can substitute 
in the slope-intercept form to obtain the equation of the boundary line:
The boundary is included, as is indicated by the line being solid, so the equality symbol is replaced by either 
or 
. To find out which one, we can test a point in the solution set - for ease, we will choose 
:
0 is less than 3 so the correct symbol is 
.
The inequality is 
.
First, we determine the equation of the boundary line. This line includes points
Since we also know the
The boundary is included, as is indicated by the line being solid, so the equality symbol is replaced by either
0 is less than 3 so the correct symbol is
The inequality is
Which equation best matches the graph of the line shown above?
Which equation best matches the graph of the line shown above?
Tap to see back →
To find an equation of a line, we will always need to know the slope of that line -- and to find the slope, we need at least two points. It looks like we have (0, -3) and (12,0), which we'll call point 1 and point 2, respectively.
Now we need to plug in a point on the line into an equation for a line. We can use either slope-intercept form or point-slope form, but since the answer choices are in point-slope form, let's use that.
Unfortunately, that's not one of the answer choices. That's because we didn't pick the same point to substitute into our equation as the answer choices did. But we can see if any of the answer choices are equivalent to what we found. Our equation is equal to:
which is the slope-intercept form of the line. We have to put all the other answer choices into slope-intercept to see if they match. The only one that works is this one:
To find an equation of a line, we will always need to know the slope of that line -- and to find the slope, we need at least two points. It looks like we have (0, -3) and (12,0), which we'll call point 1 and point 2, respectively.
Now we need to plug in a point on the line into an equation for a line. We can use either slope-intercept form or point-slope form, but since the answer choices are in point-slope form, let's use that.
Unfortunately, that's not one of the answer choices. That's because we didn't pick the same point to substitute into our equation as the answer choices did. But we can see if any of the answer choices are equivalent to what we found. Our equation is equal to:
which is the slope-intercept form of the line. We have to put all the other answer choices into slope-intercept to see if they match. The only one that works is this one:
Refer to the above diagram. If the red line passes through the point 
, what is the value of 
?
Refer to the above diagram. If the red line passes through the point
Tap to see back →
One way to answer this is to first find the equation of the line.
The slope of a line. given two points 
can be calculated using the slope formula
Set 
:
The line has slope 3 and 
-intercept 
, so we can substitute 
in the slope-intercept form:
Now substitute 4 for 
and 
for 
and solve for 
:
One way to answer this is to first find the equation of the line.
The slope of a line. given two points
Set
The line has slope 3 and
Now substitute 4 for
Refer to the above red line. A line is drawn perpendicular to that line, and with the same 
-intercept. Give the equation of that line in slope-intercept form.
Refer to the above red line. A line is drawn perpendicular to that line, and with the same
Tap to see back →
First, we need to find the slope of the above line.
The slope of a line. given two points 
can be calculated using the slope formula
Set 
:
The slope of a line perpendicular to it has as its slope the opposite of the reciprocal of 2, which would be 
. Since we want this line to have the same 
-intercept as the first line, which is the point 
, we can substitute 
and 
in the slope-intercept form:
First, we need to find the slope of the above line.
The slope of a line. given two points
Set
The slope of a line perpendicular to it has as its slope the opposite of the reciprocal of 2, which would be
Line 
includes the points 
and 
. Line 
includes the points 
and 
. Which of the following statements is true of these lines?
Line
Tap to see back →
We calculate the slopes of the lines using the slope formula.
The slope of line 
is
The slope of line 
is
The lines have the same slope, making them either parallel or identical.
Since the slope of each line is 0, both lines are horizontal, and the equation of each takes the form 
, where 
is the 
-coordinate of each point on the line. Therefore, line 
and line 
have equations 
and 
.This makes them parallel lines.
We calculate the slopes of the lines using the slope formula.
The slope of line
The slope of line
The lines have the same slope, making them either parallel or identical.
Since the slope of each line is 0, both lines are horizontal, and the equation of each takes the form
An individual's maximum heart rate can be found by subtracting his or her age from 
. Which graph correctly expresses this relationship between years of age and maximum heart rate?
An individual's maximum heart rate can be found by subtracting his or her age from
Tap to see back →
In 
form, where y = maximum heart rate and x = age, we can express the relationship as:
We are looking for a graph with a slope of -1 and a y-intercept of 220.
The slope is -1 because as you grow one year older, your maximum heart rate decreases by 1.
In
We are looking for a graph with a slope of -1 and a y-intercept of 220.
The slope is -1 because as you grow one year older, your maximum heart rate decreases by 1.
Select the equation of the line perpendicular to the graph of 
.
Select the equation of the line perpendicular to the graph of
Tap to see back →
Lines are perpendicular when their slopes are the negative recicprocals of each other such as 
. To find the slope of our equation we must change it to slope y-intercept form.
Subtract the x variable from both sides:
Divide by 4 to isolate y:
The negative reciprocal of the above slope: 
. The only equation with this slope is 
.
Lines are perpendicular when their slopes are the negative recicprocals of each other such as
Subtract the x variable from both sides:
Divide by 4 to isolate y:
The negative reciprocal of the above slope:
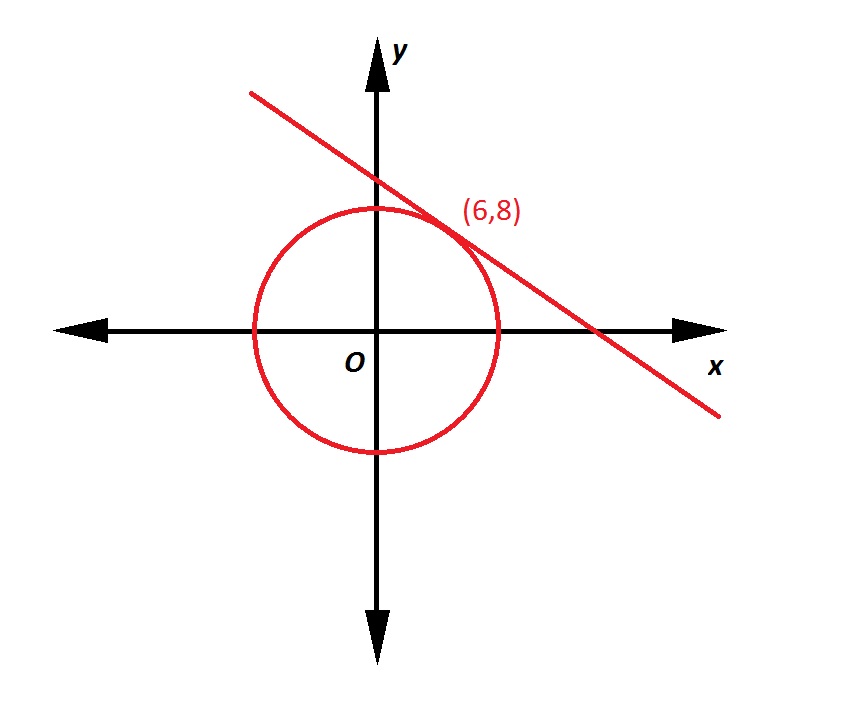
Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?
Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?
Tap to see back →
A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints 
, has slope
.
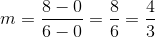The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be 
. Since it includes point 
, we can use the point-slope form of the line to find its equation:
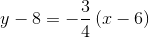
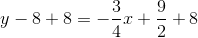
A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints
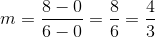
The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be
What is the range of 
?
What is the range of
Tap to see back →
The range of a function is defined as the possible values for 
, or the possible outcomes. In this function, it is not possible to get any sort of negative number as an outcome. It is possible to get zero when 
. Thus, the range is all real numbers greater than or equal to 0.
The range of a function is defined as the possible values for
is a sine curve. What are the domain and range of this function?
Tap to see back →
The domain includes the values that go into a function (the x-values) and the range are the values that come out (the 
or y-values). A sine curve represent a wave the repeats at a regular frequency. Based upon this graph, the maximum 
is equal to 1, while the minimum is equal to –1. The x-values span all real numbers, as there is no limit to the input fo a sine function. The domain of the function is all real numbers and the range is 
.
The domain includes the values that go into a function (the x-values) and the range are the values that come out (the
If 
, which of these values of 
is NOT in the domain of this equation?
If
Tap to see back →
Using 
as the input (
) value for this equation generates an output (
) value that contradicts the stated condition of 
.
Therefore 
is not a valid value for 
and not in the equation's domain:
Using
Therefore
What is the domain of the function?
What is the domain of the function?
Tap to see back →
The domain of a function is the set of possible values for the 
variable. The range would be the possible values for the solution, 
.
The value inside of a square root must be greater than or equal to zero in order to have a real solution.
Now we can solve for 
in the inequality.
Square roots have positive and negative roots, so we need to set up two results. Remember to switch the direction fo the inequality for the negative solution.
These solutions can be combined to give our final answer.
Any values of 
that are not included will result in an imaginary (impossible) answer.
The domain of a function is the set of possible values for the
The value inside of a square root must be greater than or equal to zero in order to have a real solution.
Now we can solve for
Square roots have positive and negative roots, so we need to set up two results. Remember to switch the direction fo the inequality for the negative solution.
These solutions can be combined to give our final answer.
Any values of
Which of the following does NOT belong to the domain of the function $f(x)=\frac{x^{-1}$$$+$\sqrt{1-x}$}{4x^2$+1} ?
Which of the following does NOT belong to the domain of the function $f(x)=\frac{x^{-1}$$$+$\sqrt{1-x}$}{4x^2$+1} ?
Tap to see back →
The domain of a function includes all of the values of x for which f(x) is real and defined. In other words, if we put a value of x into the function, and we get a result that isn't real or is undefined, then that value won't be in the domain.
If we let x = 0, then we will be forced to evaluate $0^{-1}$, which is equal to 1/0. The value of 1/0 is not defined, because we can never have zero in a denominator. Thus , because f(0) isn't defined, 0 cannot be in the domain of f(x).
The answer is 0.
The domain of a function includes all of the values of x for which f(x) is real and defined. In other words, if we put a value of x into the function, and we get a result that isn't real or is undefined, then that value won't be in the domain.
If we let x = 0, then we will be forced to evaluate $0^{-1}$, which is equal to 1/0. The value of 1/0 is not defined, because we can never have zero in a denominator. Thus , because f(0) isn't defined, 0 cannot be in the domain of f(x).
The answer is 0.
What is the domain of the function:
What is the domain of the function:
Tap to see back →
The domain of a function consists of all of the possible values for x. In this case, we want to make sure that we are not dividing by 
(
in the denominator), since that would make our function undefined. Having 
would make the denominator 
. Thus, that is not in our domain. There is nothing else that would make this function undefined, and thus the domain is all real numbers except 
The domain of a function consists of all of the possible values for x. In this case, we want to make sure that we are not dividing by
Find the domain of the following function.
Find the domain of the following function.
Tap to see back →
Domain represents all possible values for 
. In this situation, we want to make sure that the numbers under the square root are greater than or equal to 0. This will be the case when 
. Thus, the domain includes all real numbers such that 
.
Domain represents all possible values for
What is the range of 
?
What is the range of
Tap to see back →
The range of a function is all of the possible 
values that the equation can take. For this equation our 
value cannot be negative, as a negative number squared still gives us a positive value.
Since 
, we know that the lowest possible value that 
can reach is 
. Therefore the range is 
.
The range of a function is all of the possible
Since